A uniform rod is fixed to a rotating turntable so that its lower end is on the axis of the turntable and it makes an angle of 20% to the vertical. (The rod is thus rotating with uniform angular velocity about a vertical axis passing through one end.) If the turntable is rotating clockwise as seen from above.
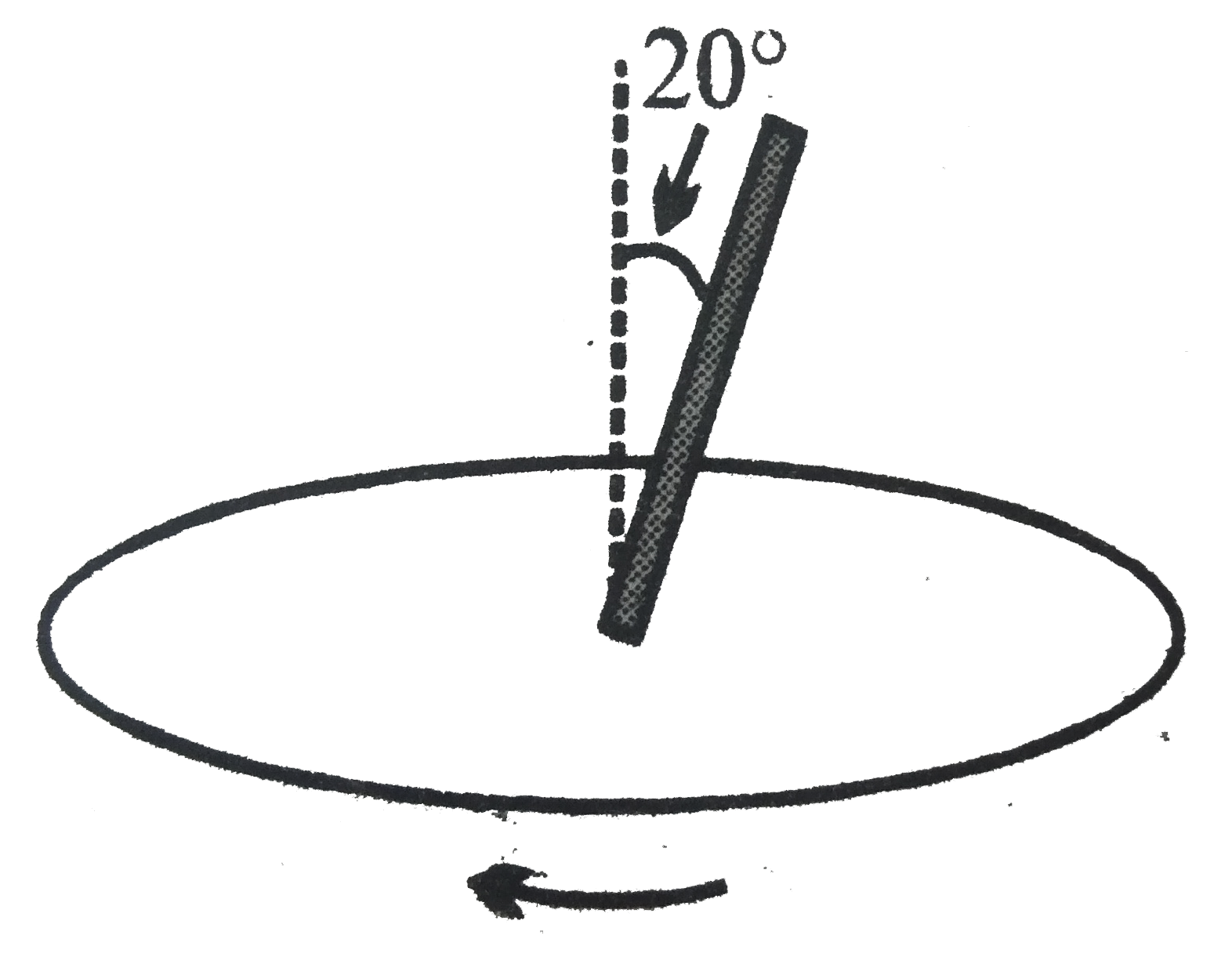 .
.
Is there a torque acts on it, and it so in what direction ?
The correct Answer is:C
The centre of mass of the rod is moving like a conical pendulam with respect to its lower and
Topper's Solved these Questions
- SYSTEM OF PARTICLESBook:NARAYNAChapter:SYSTEM OF PARTICLESExercise:Level-V
Explore 72 Videos
- PHYSICAL WORLDBook:NARAYNAChapter:PHYSICAL WORLDExercise:C.U.Q
Explore 10 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION Book:NARAYNAChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTION Exercise:EXERCISE - IV
Explore 39 Videos
Similar Questions
A uniform metal rod is rotated in horizontal plane about a vertical axis passing through its end at uniform rate. The tension in the rod is
View SolutionA thin uniform rod of mass m and length L rotates with the constant angular velocity ω about .the vertical axis passing through the rod's suspensjon point O. It describes a carried surface, then:
View Solution
Knowledge Check
A uniform rod is fixed to a rotating turntable so that its lower end is on the axis of the turntable and it makes an angle of 20% to the vertical. (The rod is thus rotating with uniform angular velocity about a vertical axis passing through one end.) If the turntable is rotating clockwise as seen from above.
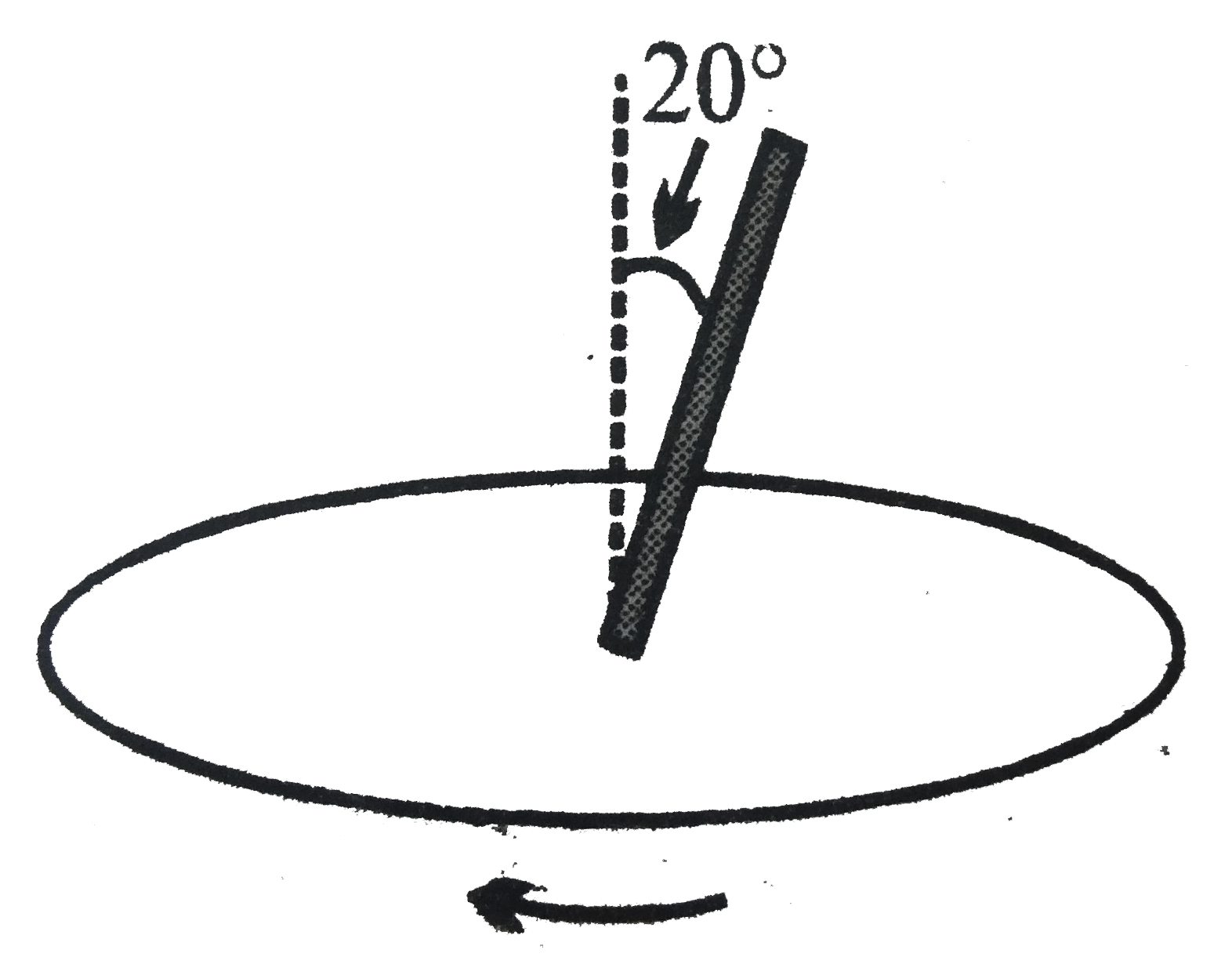 .
.
What is the direction of the rod's angular momentum vector (calculated about its lower end) ?Avertically downwardsBdown at 20∘ to the horizontalCup at 20∘ to the horizontalDvertically upwardsA rod is rotating with angular velocity ω about axis AB. Find cosθ.
 Ag2lω2Bglω2C2g(lω)2D3g2lω2
Ag2lω2Bglω2C2g(lω)2D3g2lω2A uniform rod of mass m and length l rotates in a horizontal plane with an angular velocity ω about a vertical axis passing through one end. The tension in the rod at a distance x from the axis is
A12mω2xB12mω2(1−x2l)C12mω2l(1−x2l2)D12mω2l[1−xl]
The radius of gyration of a uniform rod of length l about an axis passing through one of its ends and perpendicular to its length is
View SolutionA thin uniform copper rod of length l and cross-section area A and mass m rotates uniformly with an angular velocity ω in a horizontal plane about a vertical axis passing through one of its ends. The elongation of the rod will be
View Solutionif rod is rotated about an axis passing through its mid-point , the potential difference between the ends of rod is
View SolutionA thin uniform heavy rod of length l hangs from a horizontal axis passing through one end. The initial angular velocity ω that must be imparted to it to rotate it through 90∘ is :
View SolutionA thin rod of mass m and length 2L is made to rotate about an axis passing through its center and perpendicular to it. If its angular velocity changes from O to ω in time t, the torque acting on it is
View Solution

