A plank of mass m1 with a uniform solid sphere of mass m2 placed on it rests and a force F is applied to the plank. The acceleration of the plank provided there is no sliding between the plank and the sphere is (Fm1+n7m2) then the value of n is
The correct Answer is:2
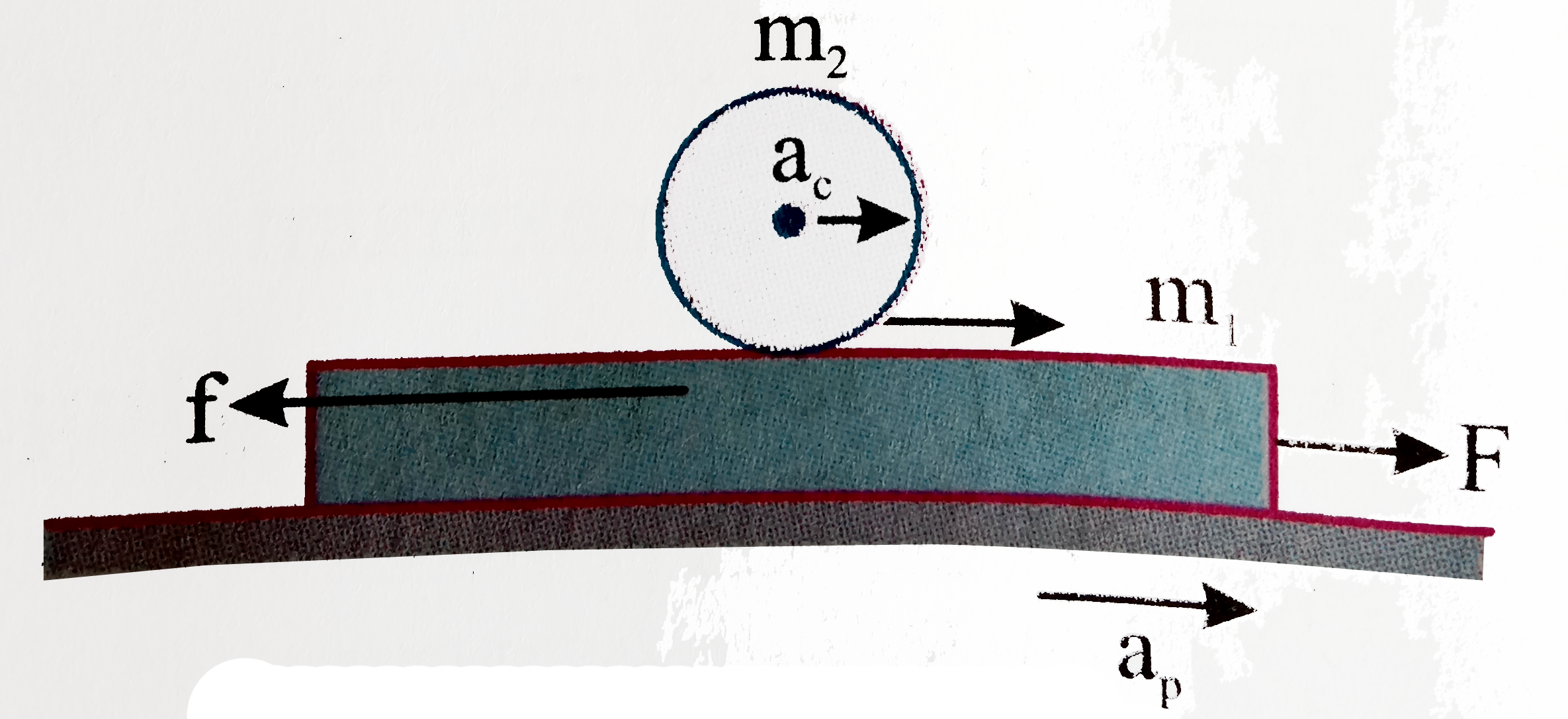
The situation is as shown in the figure
Here we have,
F−f=m1ap....(i)
and f=m2a2.....(ii)
Futher, f×r=Iα=25m2r2α
and, ap=ac+αr
Substituting the of f from equations (2)
equations (1), we get
F−ma2ac=m1ap
Now we substituting the value of ap from equations (4) in equations (5), hence
F−m2ac=m1(ac+αr).....(6)
From equation (2) and (3) or, αr=52ac
Substituting this value in equation (6), we have
or, F−m2ac=72m1ac or, F=(m2+72m1)ac or, ac=Fm2+72m1
Now, ap=ac+αr=72ac=Fm1+27m2
Topper's Solved these Questions
- SYSTEM OF PARTICLESBook:NARAYNAChapter:SYSTEM OF PARTICLESExercise:Level-V
Explore 72 Videos
- PHYSICAL WORLDBook:NARAYNAChapter:PHYSICAL WORLDExercise:C.U.Q
Explore 10 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION Book:NARAYNAChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTION Exercise:EXERCISE - IV
Explore 39 Videos
Similar Questions
A plank of mass m1 with a uniform sphere of mass m2 placed on it rests on a smooth horizontal plane. A constant horizontal force F is applied to the plank. With what acceleration will the plank and the centre of the sphere move provided there is no sliding between the plank and the sphere?
View SolutionA plank of mass m1 with a sphere of mass m2 on it rests on a smooth horizontal surface. A canstant horizontal force F is applied to the plank. With what sliding between the plank and the sphere?
[hint: Rel vel. Of the lowest point v−(2)+εR−v1=0 for no sliding)
View Solution
Knowledge Check
A plank with a uniform sphere placed on it rests on a smooth horizontal plane. The plank is pulled to the right by a constant force F. It the sphere does not slip over the plank, then
 Aboth have the same accelerationBacceleration of the centre of sphere is less than that of the plankCwork done by friction acting on the sphere is equal to its total kinetic energyDtotal kinetic energy of the system is equal to work done by the force F
Aboth have the same accelerationBacceleration of the centre of sphere is less than that of the plankCwork done by friction acting on the sphere is equal to its total kinetic energyDtotal kinetic energy of the system is equal to work done by the force FA block of mass m is placed in equilibrium on a moving plank. The maximum horizontal acceleration of the plank for μ=0.2 is:
A2m/s2B3m/s2Cdependent on the mass mDnone of theseIn Fig a sphere of radius 2m rolls on a plank. The accelerations of the sphere and the plank are indicated. The value of α is
 A2rad/s2B4rad/s2C3rad/s2D1rad/s2
A2rad/s2B4rad/s2C3rad/s2D1rad/s2
A plank of mass M is placed on a rough horizontal force F is applied on it A man of mass m rens on the plank find the acceleration of the man so that the plank does not move on the surface . The coefficent of friction between the plank and the surface is μ Assume that the man does not slip on the plank

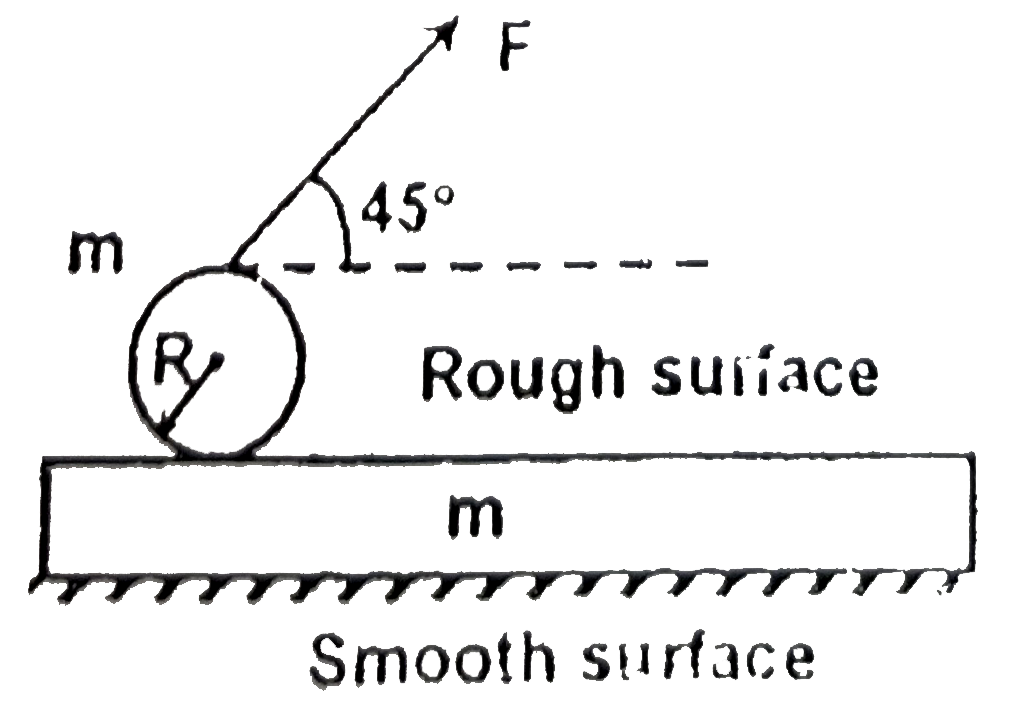
View SolutionA plank of mass m is placed on a smooth surface. Now, a uniform solid sphere of equal mass m and radius R is placed on the plank as shown in the figure. A force F is applied at topmost point of the sphere at an angle of 45∘ to the horizontal. Surface between the plank and the sphere is extremely rough so that there is no slip between the plank and the sphere. The force of firction acting between the plank and the sphere is Fk√2. Find the value of k.
View SolutionA solid sphere of mass m and radius R is placed over a plank of same mass m. There is sufficient friction between sphere and plank to prevent slipping.
Angular acceleration of sphere is
View SolutionA long horizontal plank of mass m is lying on a smooth horizontal surface. A sphere of same mass m and radius r is spinned about its own axis with angular velocity we and gently placed on the plank. The coefficient of friction between the plank and the sphere is μ. After some time the pure rolling of the sphere on the plank will start. Answer the following questions.

Find the displacement of the plank till the sphere starts pure rolling.
View SolutionA long horizontal plank of mass m is lying on a smooth horizontal surface. A sphere of same mass m and radius r is spinned about its own axis with angular velocity we and gently placed on the plank. The coefficient of friction between the plank and the sphere is μ. After some time the pure rolling of the sphere on the plank will start. Answer the following questions.
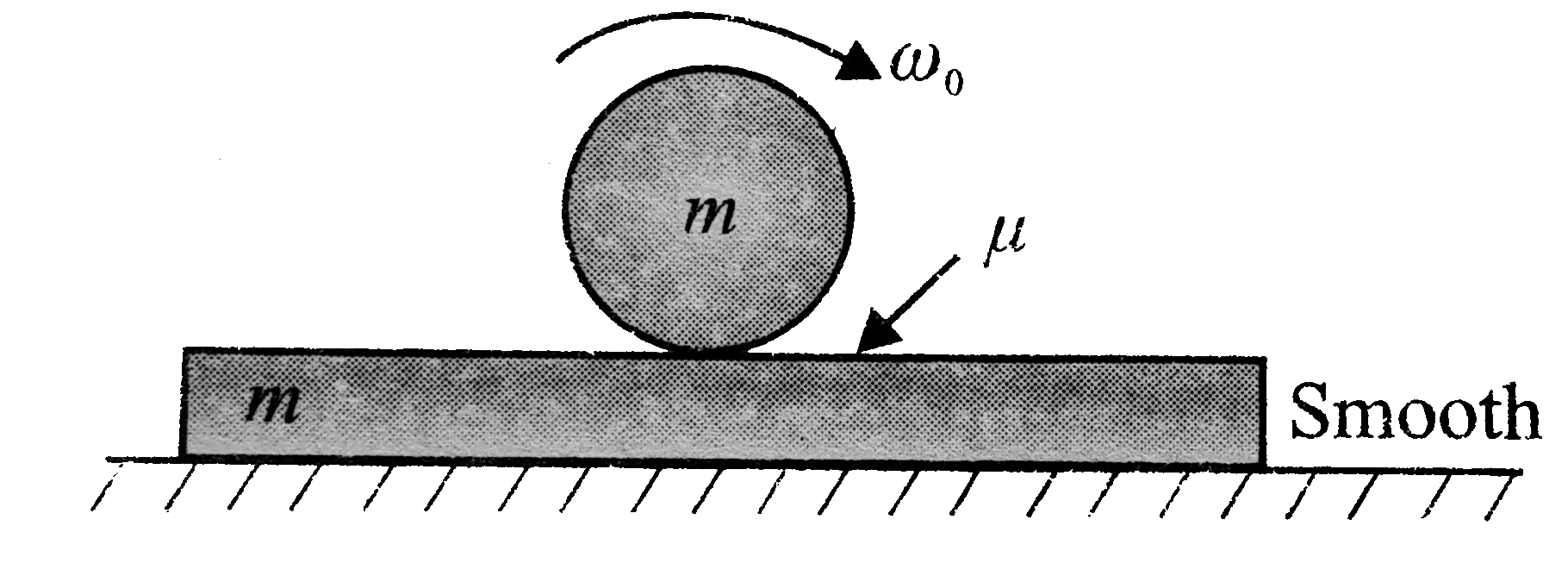
Find the velocity of the sphere after the pure rolling starts
View Solution

