A disc of mass $M$ and radius $R$ can rotate freely in a vertical plane about a horizontal axis at $O$ distance $r$ from the centre of the disc as shown in Fig. The disc is released from rest in the shown position. Answer the following questions based on the above information

Reaction force exerted by the hinge on the disc at the instant when disc rotates by an angle of $37^{\circ}$ is

$\frac{M g}{5 (R^{2} + 2 r^{2}) \times \sqrt{{g (R^{2} + 6 r^{2})}^{2} + {(4 R^{2})}^{2}}}$

$\frac{M g}{5 (R^{2} + 2 r^{2}) \times 3 (R^{2} + 6 r^{2})}$

$\frac{4 M g}{5 (R^{2} + 2 r^{2})} \times R^{2}$

$\frac{M g}{5 (R^{2} + 2 r^{2}) \times 4 R^{2}}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

From $τ = I α$
$\Rightarrow M g \times r {cos 37}^{\circ} = [\frac{M R^{2}}{2} + M r^{2}] α$
$\Rightarrow α = \frac{8 r g}{5 [R^{2} + 2 r^{2}]}$
From energy -conservation.
$\frac{I ω^{2}}{2} = M g \times r {sin 37}^{\circ}$
$\Rightarrow [\frac{M R^{2}}{2} + M r^{2}] \frac{ω^{2}}{2} = M g r \times \frac{3}{5}$
$\Rightarrow ω = \sqrt{\frac{12 g r}{5 [R^{2} + 2 r^{2}]}}$
From $F B D$ of disc,
$R_{x} - M g {sin 37}^{\circ} = M a_{r} = M ω^{2} r$

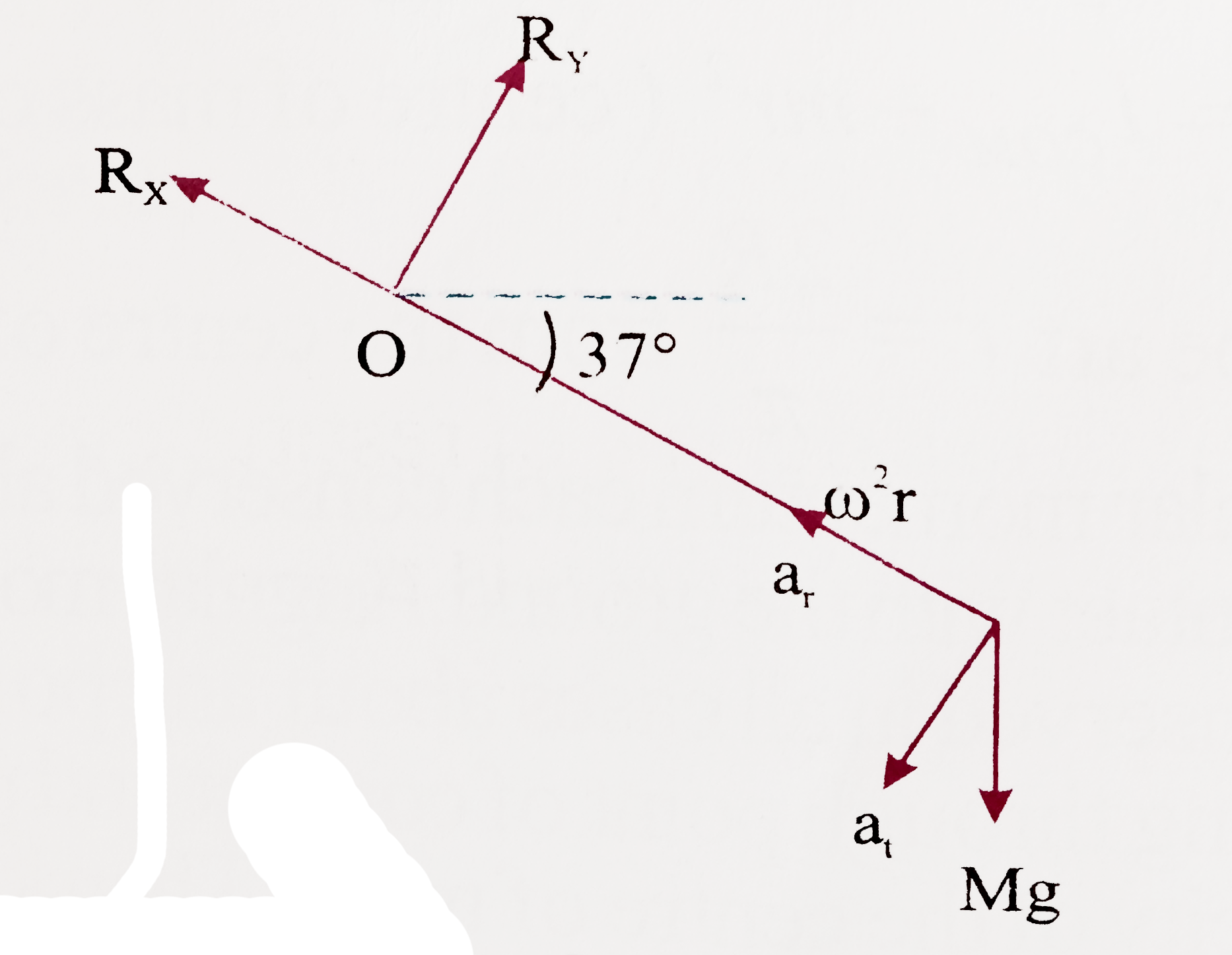
$M g {cos 37}^{\circ} - R_{y} = M a_{t} = M r α$
$\Rightarrow R_{x} = \frac{3 M g}{5} [\frac{R^{2} + 6 r^{2}}{R^{2} + 2 r^{2}}]$ ,
$R_{y} = \frac{M g}{5} [\frac{4 R^{2}}{R^{2} + 2 r^{2}}]$
$R = \sqrt{R_{x}^{2} + R_{y}^{2}} = \frac{M g}{5 [R^{2} + 2 r^{2}]}$
$[\sqrt{{g (R^{2} + 6 r^{2})}^{2} + {(4 R^{2})}^{2}}]$

Updated on:21/07/2023

Class 11 PHYSICS RIGID BODY DYNAMICS

Topper's Solved these Questions

Knowledge Check

A disc of mass $M$ and radius $R$ can rotate freely in a vertical plane about a horizontal axis at $O$ distance $r$ from the centre of the disc as shown in Fig. The disc is released from rest in the shown position. Answer the following questions based on the above information

Reaction force exerted by the hinge on the disc at this instant is
A $\frac{M g}{5 (R^{2} + 2 r^{2})} \times \sqrt{9 {(R^{2} + 6 r^{2})}^{2} + {(4 R^{2})}^{2}}$
B $\frac{M g}{5 (R^{2} + 2 r^{2})} \times 3 (R^{2} + 6 r^{2})$
C $\frac{4 M g}{5 (R^{2} + 2 r^{2})} \times R^{2}$
D $\frac{M g}{5 (R^{2} + 2 r^{2})} \times 4 R^{2}$
A disc of mass $M$ and radius $R$ can rotate freely in a vertical plane about a horizontal axis at $O$ distance $r$ from the centre of the disc as shown in Fig. The disc is released from rest in the shown position. Answer the following questions based on the above information

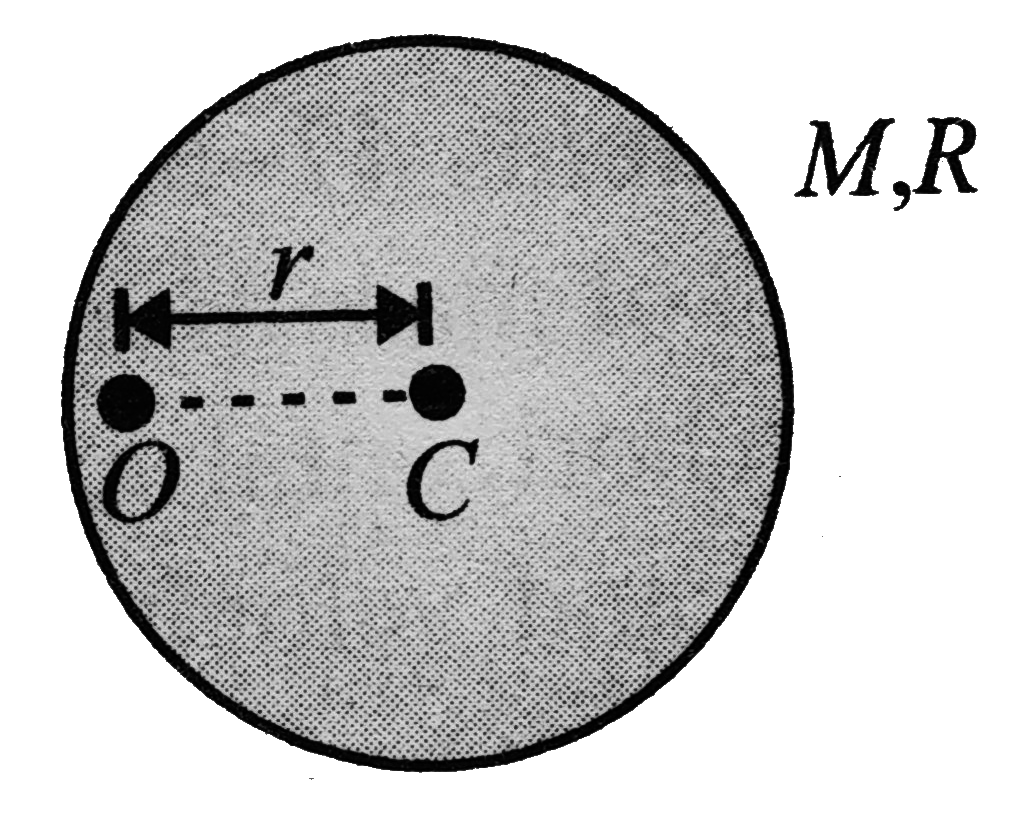
The angular velocity of the disc in the above described case is
A $\sqrt{\frac{8 g r}{5 {R^{2} + 2 r^{2}]}}$
B $\sqrt{\frac{6 g r}{5 [R^{2} + 2 r^{2}]}}$
C $\sqrt{\frac{12 g r}{5 [R^{2} + 2 r^{2}]}}$
D $\sqrt{\frac{12 g r}{5 R^{2}}}$
A disc of a mass $M$ and radius $R$ can rotate freely in vertical plane about a horizontal axis at $O$ . Distant $r$ from the centre of disc as shown in the figure. The disc is released from rest in the shown position.

The angular acceleration of disc when $O C$ rotates by an angles of $37^{\circ}$ is
A $\frac{8 r g}{5 [R^{2} + 2 r^{2}]}$
B $\frac{5 r g}{4 [R^{2} + 2 r^{2}]}$
C $\frac{10 r g}{3 [R^{2} + 2 r^{2}]}$
D $\frac{8 r g}{5 R^{2}}$

NARAYNA-SYSTEM OF PARTICLES-Level-VI

Home
Ask Doubt
Profile

The correct Answer is:A

Topper's Solved these Questions

Similar Questions

Knowledge Check

A disc of a mass M and radius R can rotate freely in vertical plane about a horizontal axis at O. Distant r from the centre of disc as shown in the figure. The disc is released from rest in the shown position. The angular acceleration of disc when OC rotates by an angles of 37∘ is

NARAYNA-SYSTEM OF PARTICLES-Level-VI