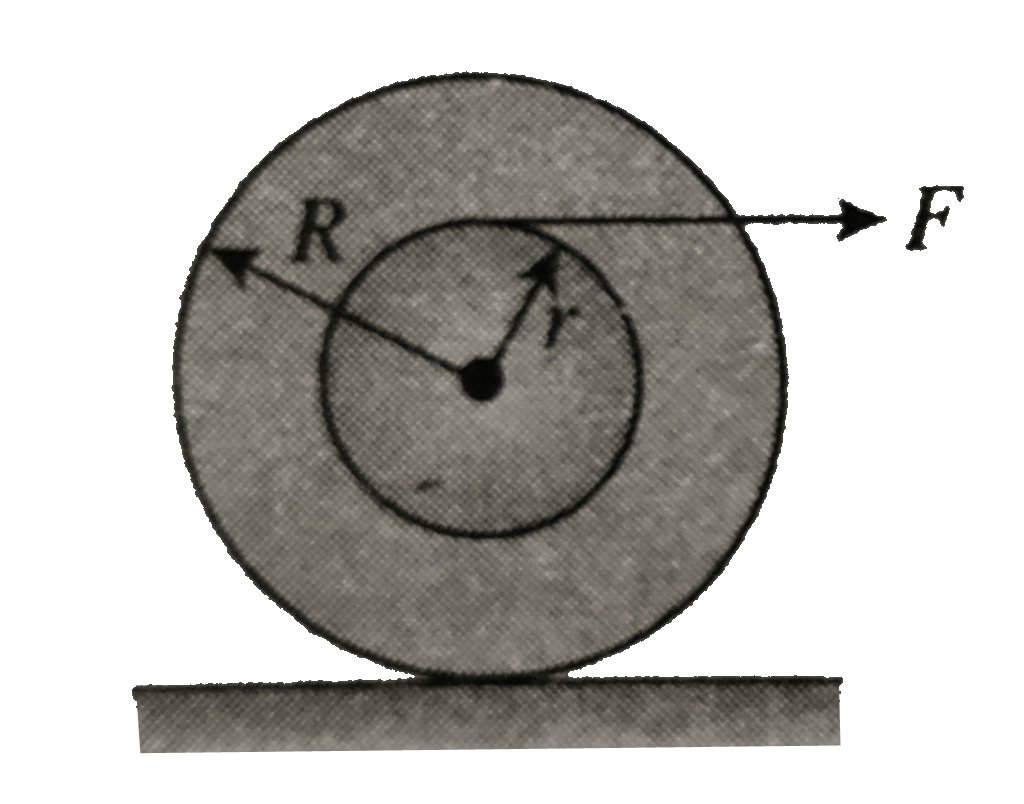
A wheel of radius R, mass m with an axle of radius r is placed on a ho

A wheel of radius $R$ , mass $m$ with an axle of radius $r$ is placed on a horizontal surface. Its moment of inertia is $I = m R^{2}$ . Unwinding a rope from its axel a force $F$ is applied to pull it along a horizontal surface. The friction is sufficient enough for its pure rolling $(∠ θ = 0^{\circ})$

Find the condition for which frictional force acts in backward direction
A $(I / m) > R r$
B $(2 I / m) > R r$
C $(\frac{I \sqrt{2}}{m}) > R r$
D $(\frac{I}{m \sqrt{2}}) > R r$
A wheel of radius $R$ , mass $m$ with an axle of radius $r$ is placed on a horizontal surface. Its moment of inertia is $I = m R^{2}$ . Unwinding a rope from its axel a force $F$ is applied to pull it along a horizontal surface. The friction is sufficient enough for its pure rolling $(∠ θ = 0^{\circ})$

Find the linear acceleration of the wheel
A $\frac{F [I / m - R r]}{[(I / m) + r^{2}]}$
B $\frac{2 F [(I / m) - R r]}{[(1 / m) + r^{2}]}$
C $\frac{F [(2 I / m) - \sqrt{2} R r]}{[(I / m) + r^{2}]}$
D $\frac{F [(I \sqrt{2} / m) - R r]}{[(I / m) + r^{2}]}$
A solid cylinder of mass M and radius R rolls without slipping on a flat horizontal surface. Its moment of inertia about the line of contact is ?
A $\frac{M R^{2}}{2}$
B $M R^{2}$
C $\frac{3}{2} M R^{2}$
D $2 M R^{2}$

The correct Answer is:A