An uniform rod of mass m=30kg and length l=0.80m is free to rotate about a horizontal axis O passing through its centre. A particle P of mass M=11.2kg falls vertically through a height h=36245m and collides elastically with the rod at a distance l4 from O. at the instant of collision the rod was stationary and was at angle α=37∘ with horizontal as shown in figure
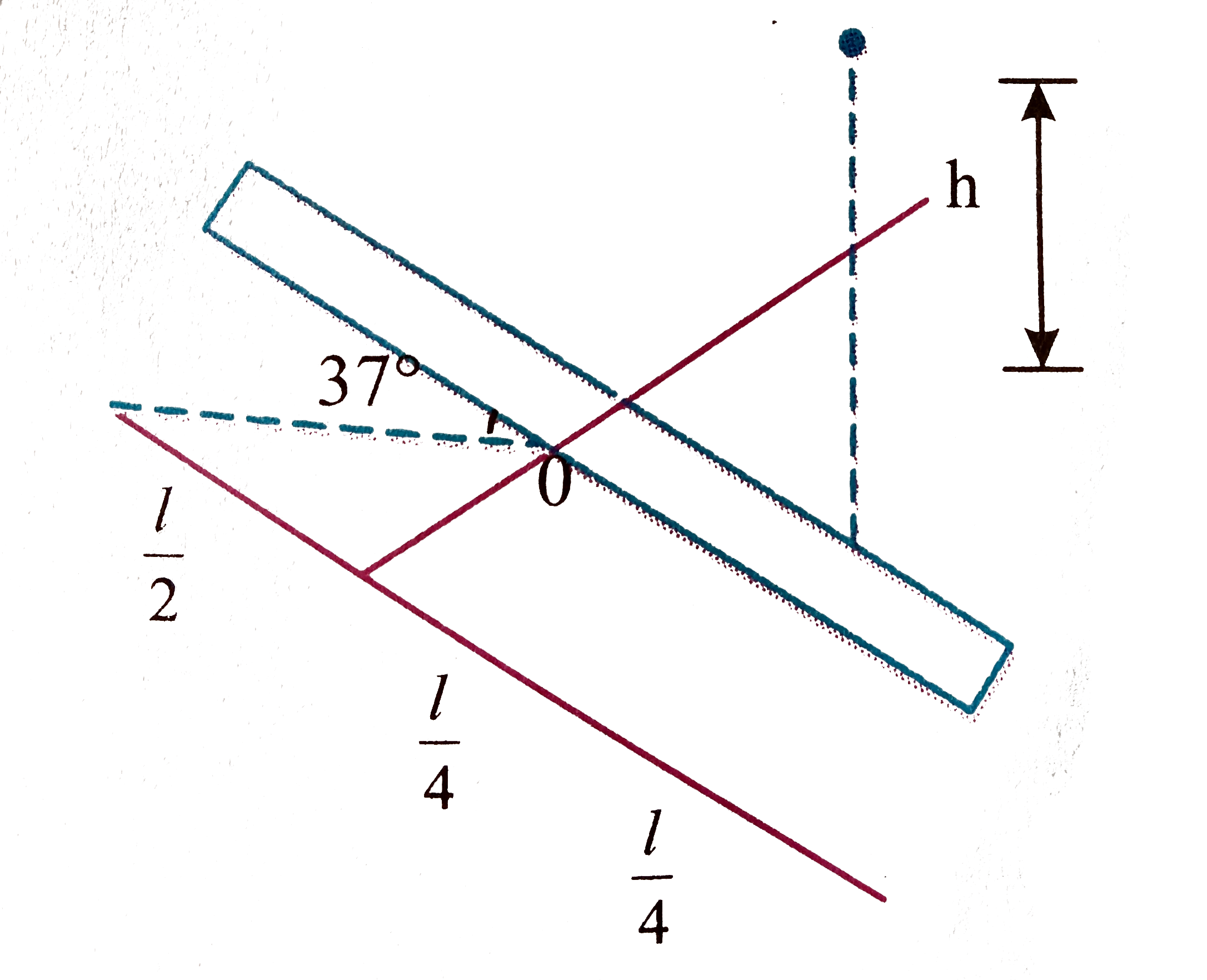
Calculate velocity of the rod just after collision is
1rad/s
3rad/s
2rad/s
4rad/s
The correct Answer is:D
Velcity component of particle, normal to rod(just after collision) is
υn=J−Mυ0cosαM
Since, the collision is elastic, therefore, there is normal loss of kinetic energy during collision. Hence kinetic energy of system of rod and particle just after collision=kinetic energy of particle just before collision.
∴12Iω2+12M(υ2t+υ2n)=12μψlon20
J=24Ns
∴ From equation (1)ω=3rad/sectangential component of velocity of particle υt=υ0sinα=√2ghsin37∘=3635ms−1
Topper's Solved these Questions
- SYSTEM OF PARTICLESBook:NARAYNAChapter:SYSTEM OF PARTICLESExercise:Level-V
Explore 72 Videos
- PHYSICAL WORLDBook:NARAYNAChapter:PHYSICAL WORLDExercise:C.U.Q
Explore 10 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION Book:NARAYNAChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTION Exercise:EXERCISE - IV
Explore 39 Videos
Similar Questions

A uniform rod of mass m is rotated about an axis passing through point O as shown. Find angular momentum of the rod about rotational law.
View SolutionA thin uniform rod of length l and mass m is swinging freely about a horizontal axis passing through its end. Its maximum angular speed is ω. Its centre of mass rises to a maximum height of -
View Solution
Knowledge Check
An uniform rod of mass m=30kg and length l=0.80m is free to rotate about a horizontal axis O passing through its centre. A particle P of mass M=11.2kg falls vertically through a height h=36245m and collides elastically with the rod at a distance l4 from O. at the instant of collision the rod was stationary and was at angle α=37∘ with horizontal as shown in figure
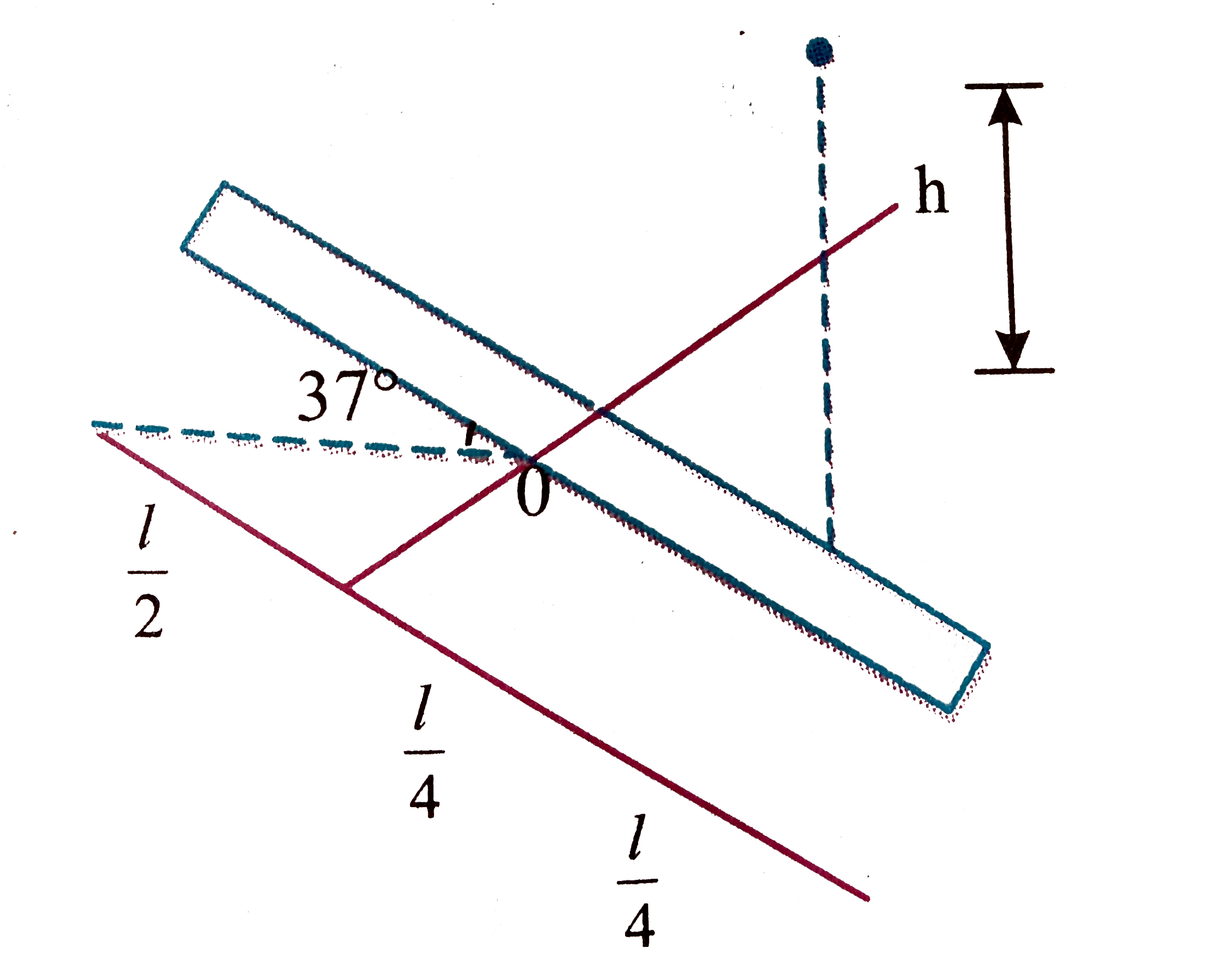
Velocity of particle P after collision (g=10ms−2)A79ms−1B7ms−1C97ms−1D1ms−1The M.I. of thin uniform rod of mass 'M' and length 'l' about an axis passing through its centre and perpendicular to its length is
AMl2BMl2/3CMl2/2DMl2/12A thin uniform rod of mass M and length L. Find the radius of gyration for rotation about an axis passing through a point at a distance ofL4 from centre and perpendicular to rod.
A√748LB√548LC√724LD√1924L
A thin uniform rod of length l and mass m is swinging freely about a horizontal axis passing through its end. Its maximum angular speed is ω. Its cenre of mass rises to a maximum height of :
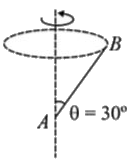
View SolutionA rod AB of mass m and length l is rotating about a vertical axis as shown. It's moment of inertia about this axis is :
View SolutionThe moment of inertia of a uniform rod of length 2l and mass m about an axis xy passing through its centre and inclined at an angle α is

View SolutionMoment of inertia of a rod of mass M and length L about an axis passing through a point midway between centre and end is
View SolutionA uniform rod of mass m and length l rotates in a horizontal plane with an angular velocity ω about a vertical axis passing through one end. The tension in the rod at a distance x from the axis is
View Solution

