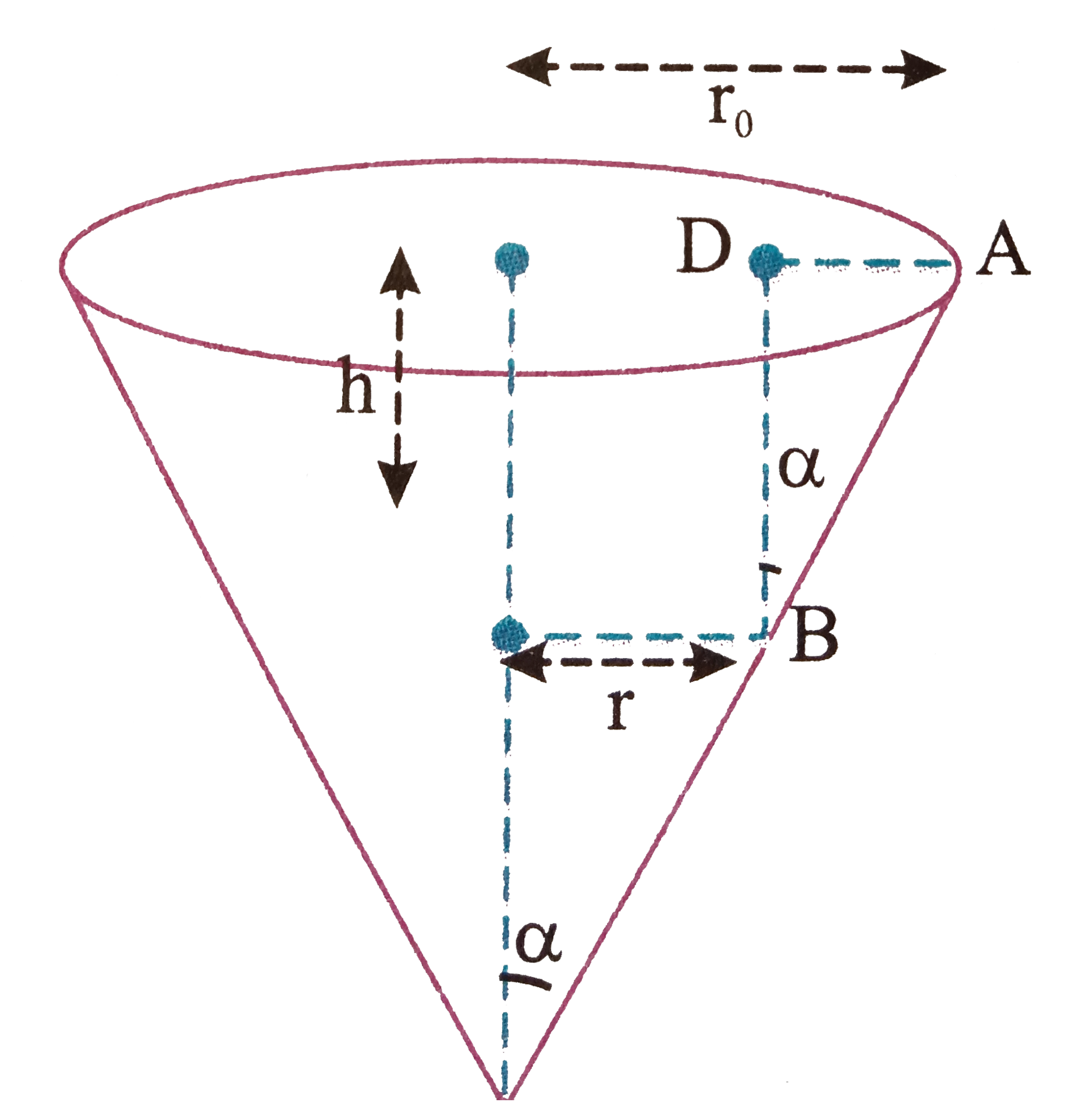
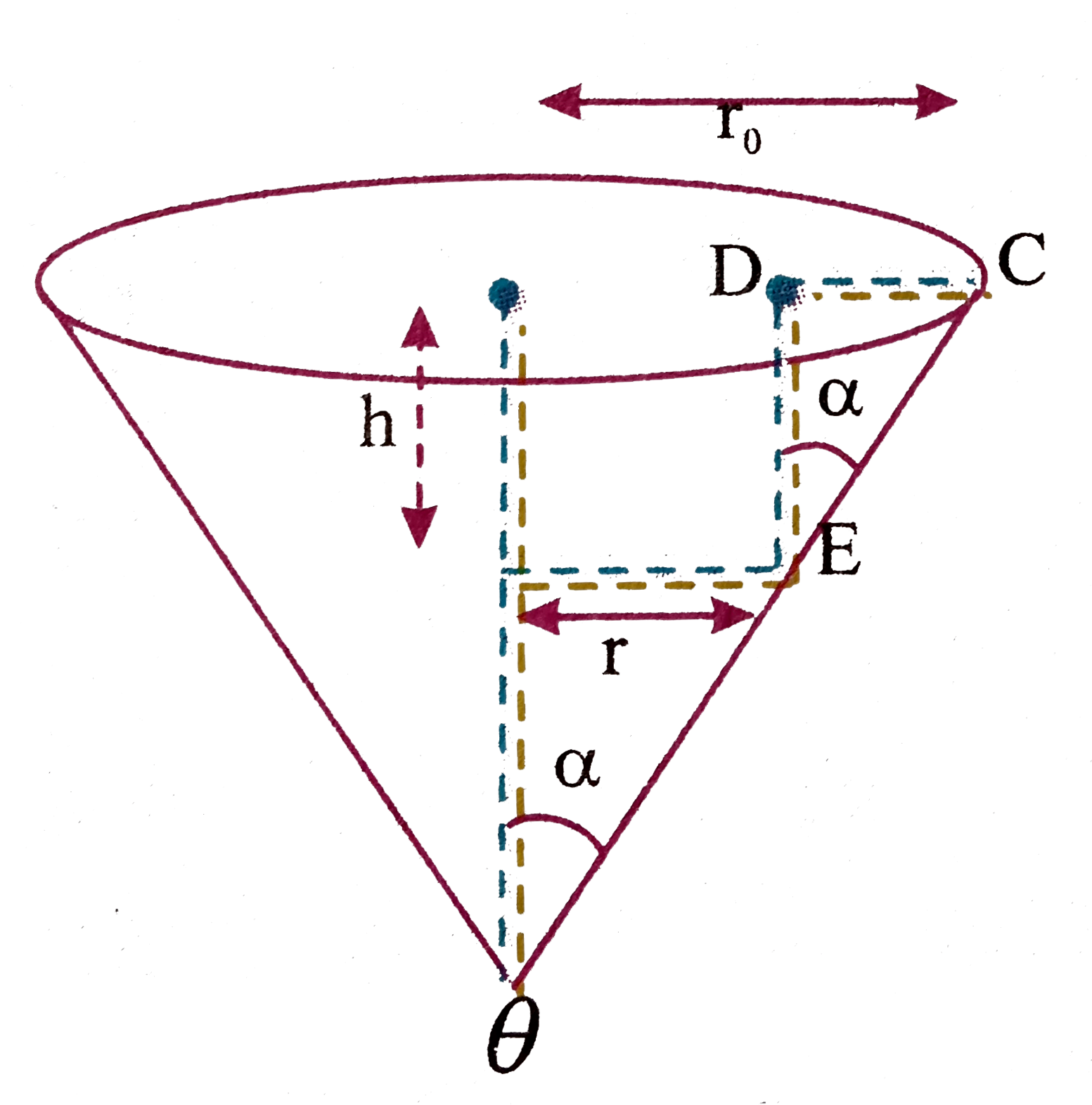
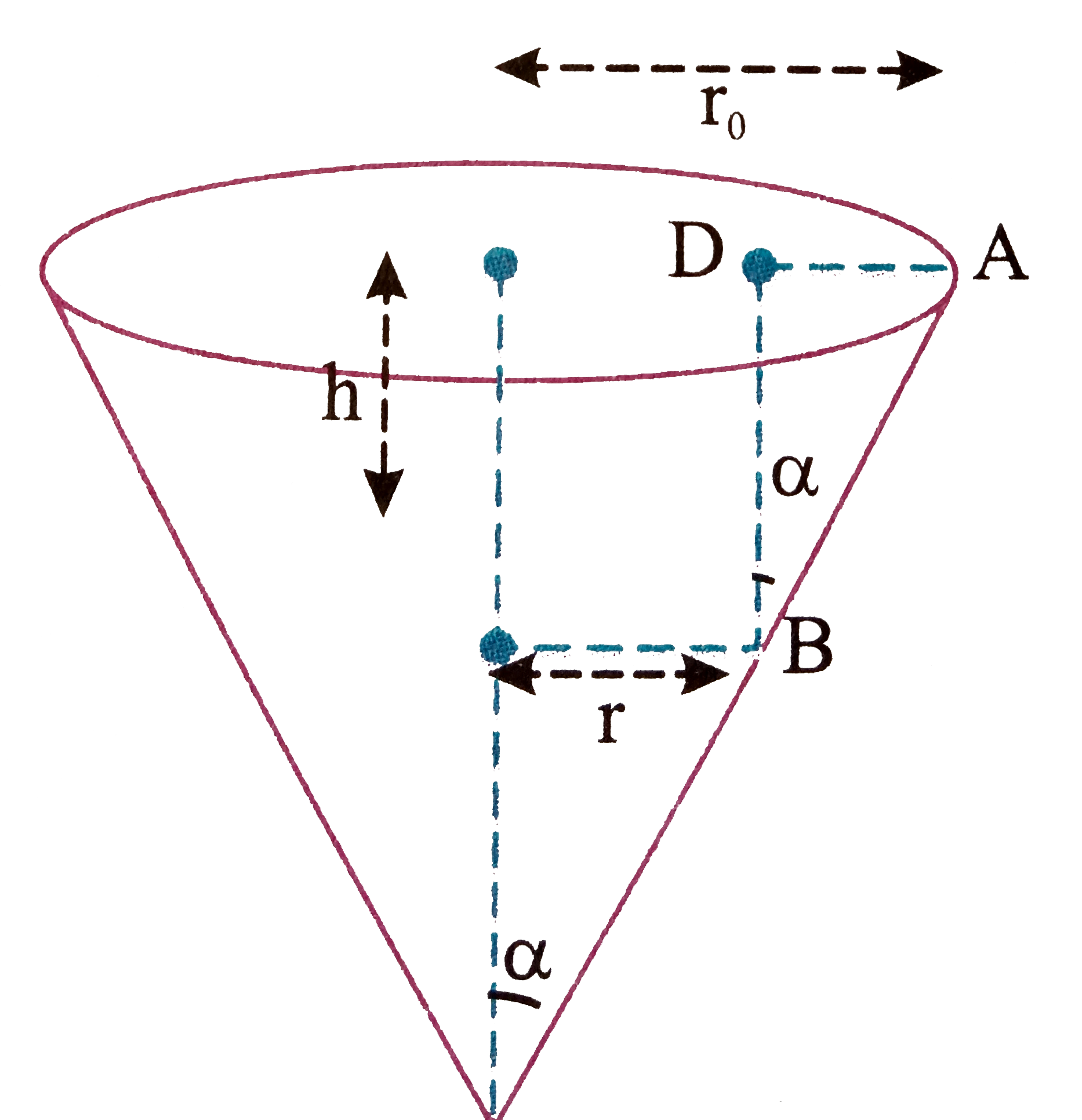
A small particle of mass m is given an initial velocity v0 tangent to the horizontal rim of a smooth cone at a radius r0 from the vertical slides to point B, a vertical distance h below A and a distance r from the vertical centreline, its velocity v makes an angle θ with the horizontal tangent to the cone through B.
The minimum value of v0 for which particle will be moving in a horizontal circle of radius r0.
√2gr0tanα
√gr02tanα
√gr0tanα
√4gr0tanα
The correct Answer is:C
From angular momentum conservation about axis of cone.
mv0r0=mvrcosθ
v0r0=vrcosθ.....(i)
from energy conservation E1=E2
12mv20+mgh=12mv2+0,v=√v20+2gh
r0−r=htanα,r=(r0−htanα)
From equations (i)
Eliminating v and substituting r=r0−htanα
v0r0=√v20+2gh(r0−htanα)cosθ
cosθ=v0r0√v20+2gh(r0−htanα)
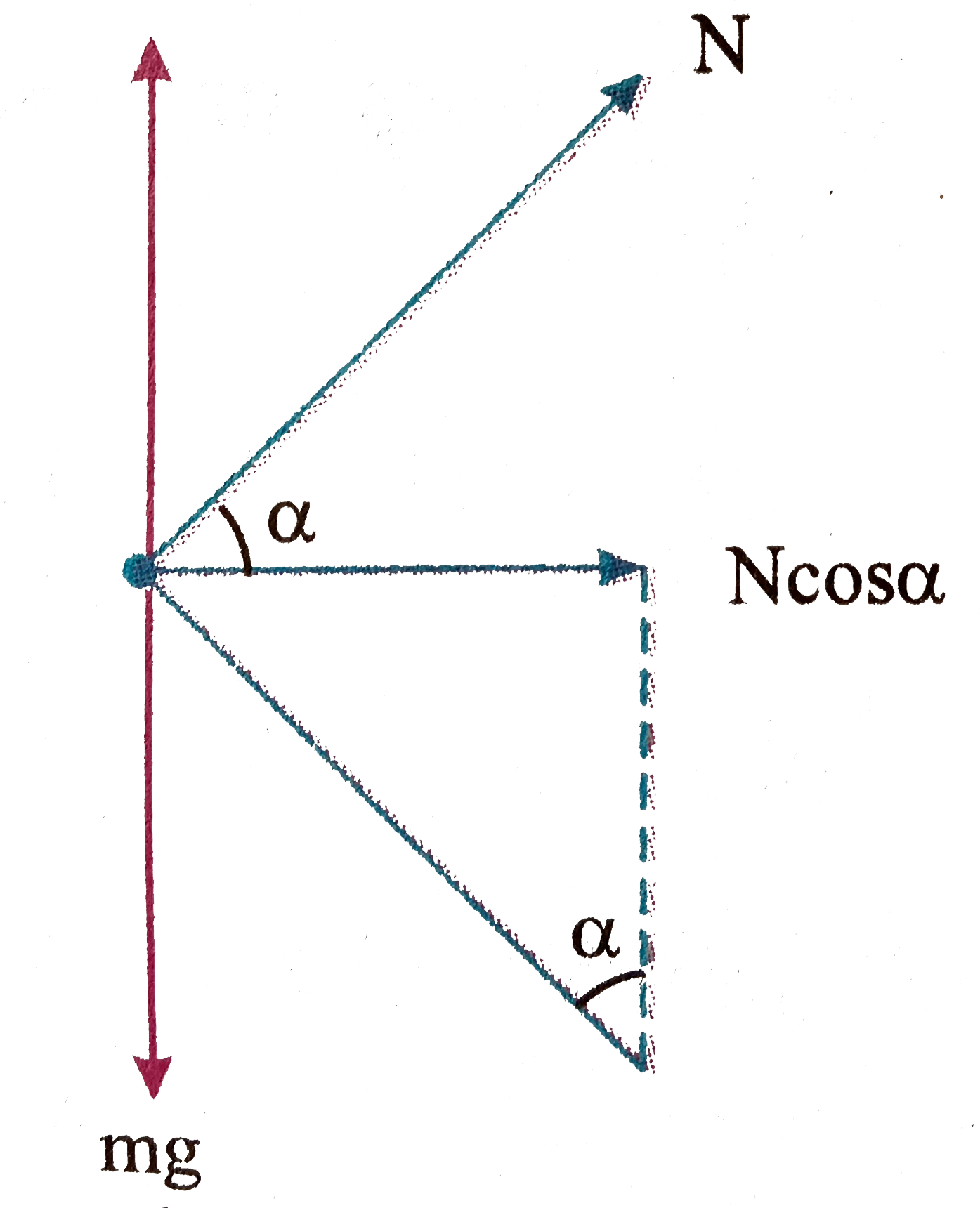
Nsinα=mg....(ii)Ncosα=mv20r0.....(iii)
Solving (ii) and (iii) tanα=gr0v20
J.a=IGω=112(3m)(4a2).ω=4ma2ω
Topper's Solved these Questions
- SYSTEM OF PARTICLESBook:NARAYNAChapter:SYSTEM OF PARTICLESExercise:Level-V
Explore 72 Videos
- PHYSICAL WORLDBook:NARAYNAChapter:PHYSICAL WORLDExercise:C.U.Q
Explore 10 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION Book:NARAYNAChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTION Exercise:EXERCISE - IV
Explore 39 Videos
Similar Questions
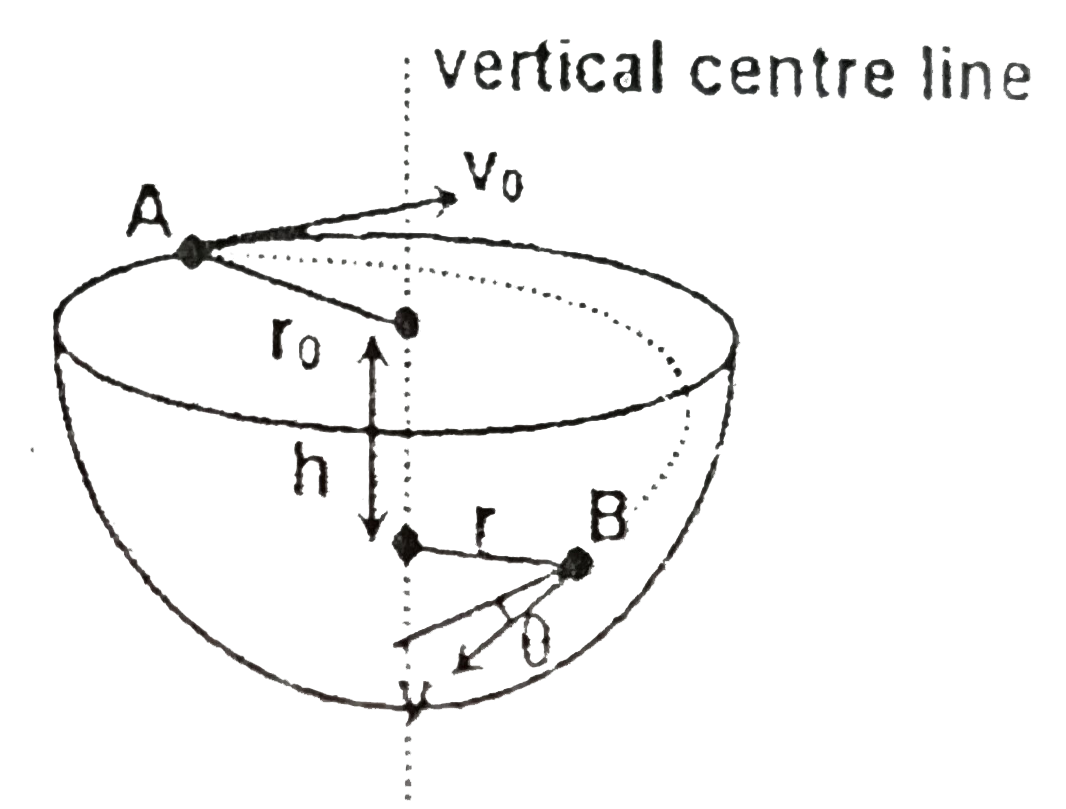
A small mass particle is projected with an initial velocity v0 tangent to the horizontal rim of smooth hemispherical bowl at a radius r0 from the vertical centre line, as shown at point A. As the particle slide past point B, a distance h below A and distance r from the vertical centre line, its velocity v makes an angle θ with the horizontal tangent to the bowl through B. Determine θ.

View SolutionA small particle is given an initial velocity v0=10m/s along the tangent to the brim of a fixed smooth hemisphere bowl of radius r0=15√2m as shown in the figure. The particle slides on the inner surface and reaches point B, a vertical distance h=15m below A and a distance r from the vertical centerline, where its velocity v makes an angle θ with the horizontal tangent to the bowl through B. If θ=15K∘. Find the value of K. (take g=10m/s2)
View Solution
Knowledge Check
A small particle of mass m is given an initial velocity v0 tangent to the horizontal rim of a smooth cone at a radius r0 from the vertical slides to point B, a vertical distance h below A and a distance r from the vertical centreline, its velocity v makes an angle θ with the horizontal tangent to the cone through B.
The value of θ is
 Acos−1(v0r0)(r0−htanα)√v20+2ghBcos−1(v0r0)(r0+htanα)√v20+2ghCcos−1(v0r0)(r0+htanα)√v20−2ghDcos−1(v0r0)r0√v20+2gh
Acos−1(v0r0)(r0−htanα)√v20+2ghBcos−1(v0r0)(r0+htanα)√v20+2ghCcos−1(v0r0)(r0+htanα)√v20−2ghDcos−1(v0r0)r0√v20+2ghA small particle of mass m is given an initial velocity v0 tangent to the horizontal rim of a smooth cone at a radius r0 from the vertical slides to point B, a vertical distance h below A and a distance r from the vertical centreline, its velocity v makes an angle θ with the horizontal tangent to the cone through B.
The speed of particle at point B
 A√v20+2ghB√v20−2ghC√v20+ghD√2v20+2gh
A√v20+2ghB√v20−2ghC√v20+ghD√2v20+2ghAn arrow shots from a bow with velocity v at an angle θ with the horizontal range R . Its range when it is projected at angle 2θ with the same velocity is
A2RBR2C2Rcos2θDR2cos2θ
A small particle is given an initial velocity v0=10m/s along the tangent to the brim of a fixed smooth hemisphere bowl of radius r0=15√2m as shown in the figure. The particle slides on the inner surface and reaches point B, a vertical distance h=15m below A and a distance r from the vertical centerline, where its velocity v makes an angle θ with the horizontal tangent to the bowl through B. If θ=15K∘. Find the value of K. (take g=10m/s2)

View SolutionA particle is thrown with an initial speed v0 at an angle α to the horizontal. Find the radius of curvature r at the highest point of its path, and its ratios to the maximum height H and to the distance L of the particle's flight.
View SolutionA particle is projected with a velocity u making an angle θ with the horizontal. At any instant its velocity becomes v which is perpendicular to the initial velocity u. Then v is
View SolutionA small particle of mass m is given an initial high velocity in the horizontal plane and winds its cord around the fixed vertical shaft of radius a. All motion occurs essentially in horizontal plane. If the angular velocity of the cord is when the distance from the particle to the tangency point is r0, then the angular velocity of the cord after it has turned through an angle is.

View SolutionA particle is projected with velocity v at an angle of θ with horizontal. The average angular velocity of the particle from the point of projection to impact equals:
View Solution

