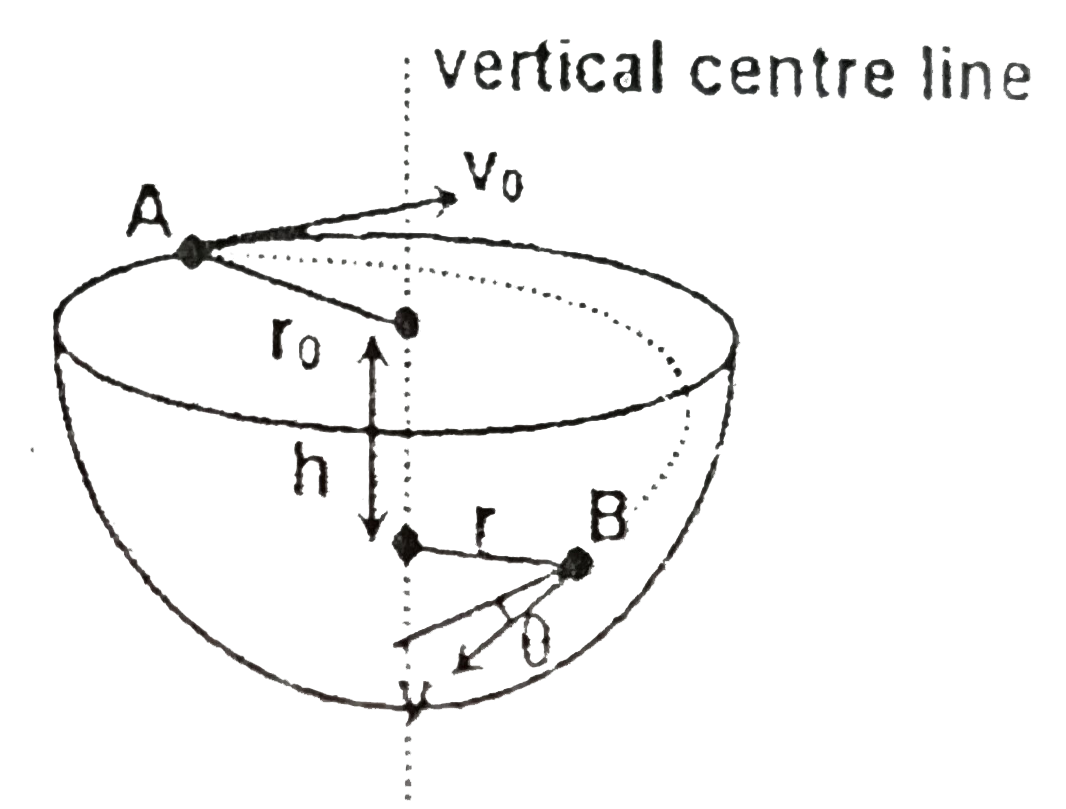
A small mass particle is projected with an initial velocity v0 tangent to the horizontal rim of smooth hemispherical bowl at a radius r0 from the vertical centre line, as shown at point A. As the particle slide past point B, a distance h below A and distance r from the vertical centre line, its velocity v makes an angle θ with the horizontal tangent to the bowl through B. Determine θ.

The forces on the particle are its weight and the normal reaction exerted by the surface of the bowl. Neither force exers a moment about the axis O−O', so that angular momentum is conserved about that axis thus,
mv0r0=mvrcosθ
Also energy is coserved so that E1=E2. thus
12mv20+mgh=12mv2+0
v=√v20+2gh
Eliminating v and substituting r2−r20−h2 give
v0r0=√v20+2gh√v20−h2cosθ
θ=cos−11√1+2ghv20√1−h2r20
Topper's Solved these Questions
- RIGID BODY DYNAMICS 2Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 2Exercise:Subjective
Explore 19 Videos
- RIGID BODY DYNAMICS 2Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 2Exercise:Single Correct
Explore 142 Videos
- RIGID BODY DYNAMICS 2Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 2Exercise:Exercise 3.3
Explore 21 Videos
- RIGID BODY DYNAMICS 1Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 1Exercise:Integer
Explore 11 Videos
- SOUND WAVES AND DOPPLER EFFECTBook:CENGAGE PHYSICSChapter:SOUND WAVES AND DOPPLER EFFECTExercise:Integer
Explore 16 Videos
Similar Questions
A small mass particle is projected with an initial velocity v0 tangent to the horizontal rim of smooth hemispherical bowl at a radius r0 from the vertical centre line, as shown at point A. As the particle slide past point B, a distance h below A and distance r from the vertical centre line, its velocity v makes an angle θ with the horizontal tangent to the bowl through B. Determine θ.

View SolutionA small particle is given an initial velocity v0=10m/s along the tangent to the brim of a fixed smooth hemisphere bowl of radius r0=15√2m as shown in the figure. The particle slides on the inner surface and reaches point B, a vertical distance h=15m below A and a distance r from the vertical centerline, where its velocity v makes an angle θ with the horizontal tangent to the bowl through B. If θ=15K∘. Find the value of K. (take g=10m/s2)
View Solution
Knowledge Check
A small particle of mass m is given an initial velocity v0 tangent to the horizontal rim of a smooth cone at a radius r0 from the vertical slides to point B, a vertical distance h below A and a distance r from the vertical centreline, its velocity v makes an angle θ with the horizontal tangent to the cone through B.
The speed of particle at point B
 A√v20+2ghB√v20−2ghC√v20+ghD√2v20+2gh
A√v20+2ghB√v20−2ghC√v20+ghD√2v20+2ghA small particle of mass m is given an initial velocity v0 tangent to the horizontal rim of a smooth cone at a radius r0 from the vertical slides to point B, a vertical distance h below A and a distance r from the vertical centreline, its velocity v makes an angle θ with the horizontal tangent to the cone through B.
The value of θ is
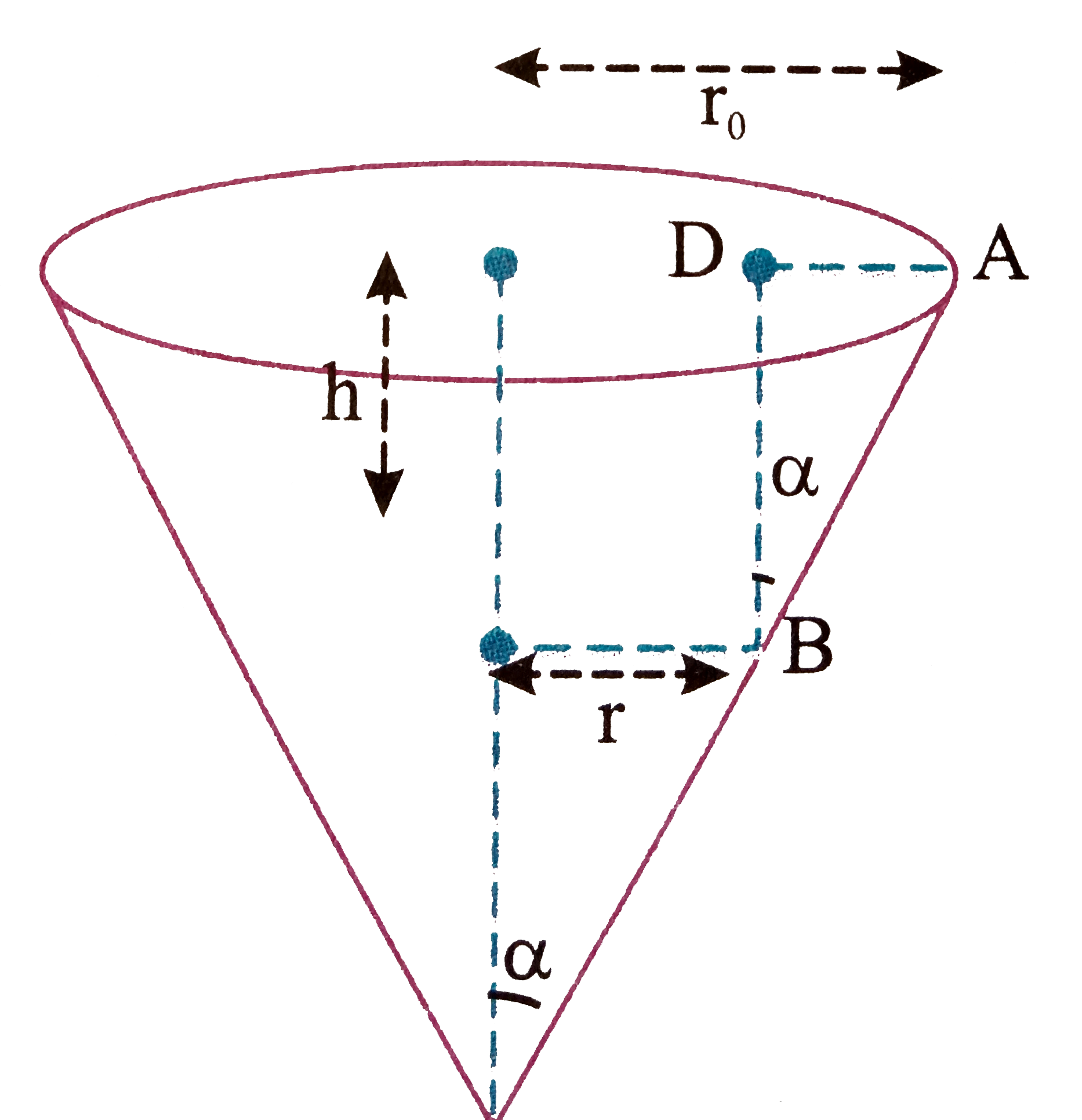 Acos−1(v0r0)(r0−htanα)√v20+2ghBcos−1(v0r0)(r0+htanα)√v20+2ghCcos−1(v0r0)(r0+htanα)√v20−2ghDcos−1(v0r0)r0√v20+2gh
Acos−1(v0r0)(r0−htanα)√v20+2ghBcos−1(v0r0)(r0+htanα)√v20+2ghCcos−1(v0r0)(r0+htanα)√v20−2ghDcos−1(v0r0)r0√v20+2ghA small particle of mass m is given an initial velocity v0 tangent to the horizontal rim of a smooth cone at a radius r0 from the vertical slides to point B, a vertical distance h below A and a distance r from the vertical centreline, its velocity v makes an angle θ with the horizontal tangent to the cone through B.
The minimum value of v0 for which particle will be moving in a horizontal circle of radius r0.
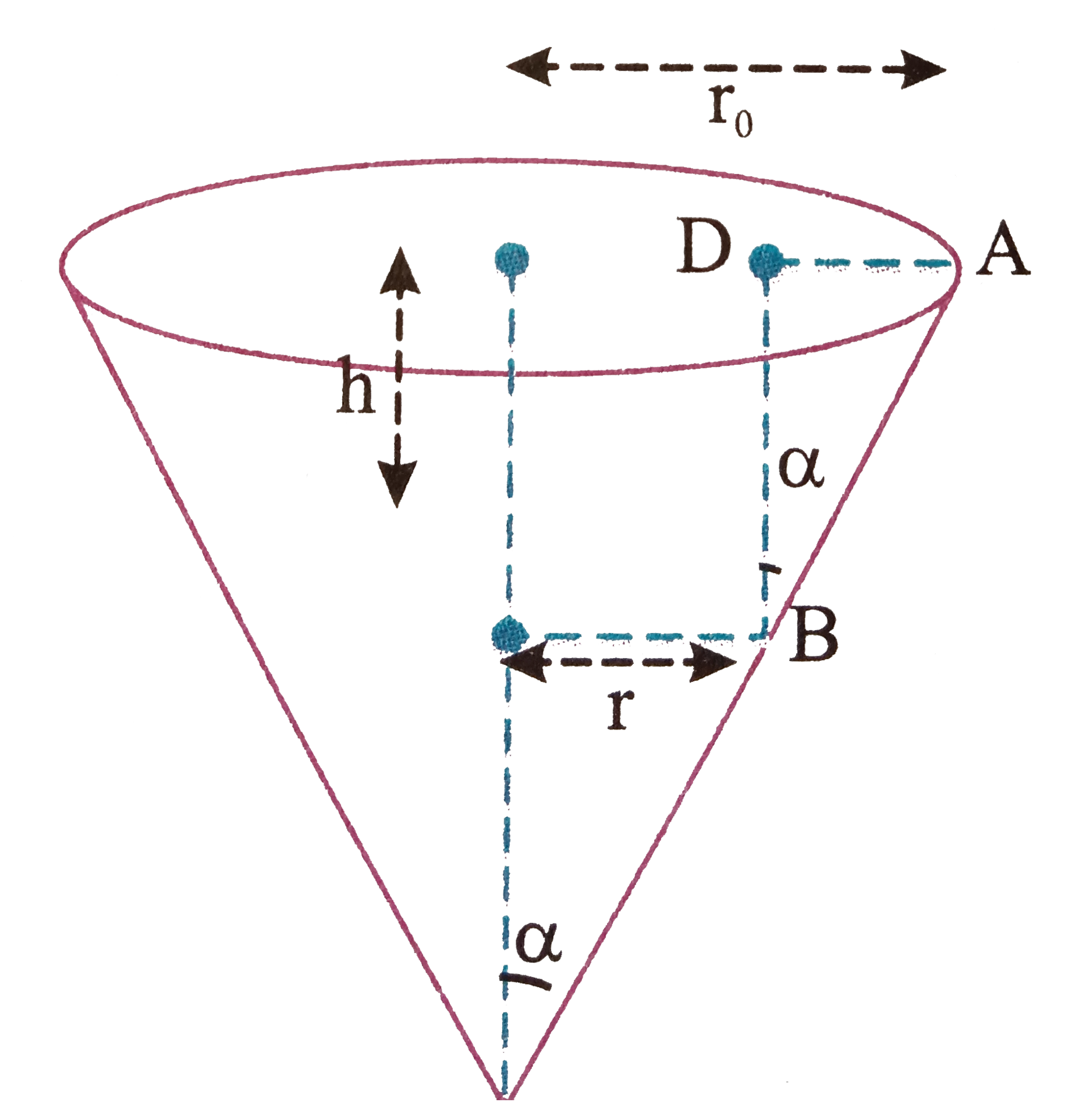 A√2gr0tanαB√gr02tanαC√gr0tanαD√4gr0tanα
A√2gr0tanαB√gr02tanαC√gr0tanαD√4gr0tanα
A small particle is given an initial velocity v0=10m/s along the tangent to the brim of a fixed smooth hemisphere bowl of radius r0=15√2m as shown in the figure. The particle slides on the inner surface and reaches point B, a vertical distance h=15m below A and a distance r from the vertical centerline, where its velocity v makes an angle θ with the horizontal tangent to the bowl through B. If θ=15K∘. Find the value of K. (take g=10m/s2)

View SolutionThe distance of the centre of mass of a hemispherical shell of radius R from its centre is
View SolutionA projectile is projected with a velocityv0 at an angle θ with the horizontal as shown in figure. The angular momentum of particle about the origin:

View SolutionA particle is projected at t=0 with velocity u at angle θ with the horizontal. Then the ratio of the tangential acceleration and the radius of curvature at the point of projection is :
View SolutionA particle is projected with velocity v at an angle θ aith horizontal. The average angle velocity of the particle from the point of projection to impact equals
View Solution

