A linear impulse ∫Fdt acts at a point C of the smooth rod AB. The value of x is so that the end A remains stationary just after the impact is

l4
l3
l6
l5
The correct Answer is:C
Let J be the impulse acting on the rod J=mmvcm,Jx=112ml2ω. Since the end A is stationary VA=Vcm−12ω=Jm−(12Jxml2)l2=0
Topper's Solved these Questions
- SYSTEM OF PARTICLESBook:NARAYNAChapter:SYSTEM OF PARTICLESExercise:Level-V
Explore 72 Videos
- PHYSICAL WORLDBook:NARAYNAChapter:PHYSICAL WORLDExercise:C.U.Q
Explore 10 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION Book:NARAYNAChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTION Exercise:EXERCISE - IV
Explore 39 Videos
Similar Questions
A uniform rod AB of length L and mass M is lying on a smooth table. A small particle if mass m strike the rod with velocity v0 at point C at a distance comes to rest after collision. Then find the value of x, so that point A of the rod remains stationary just after collision.
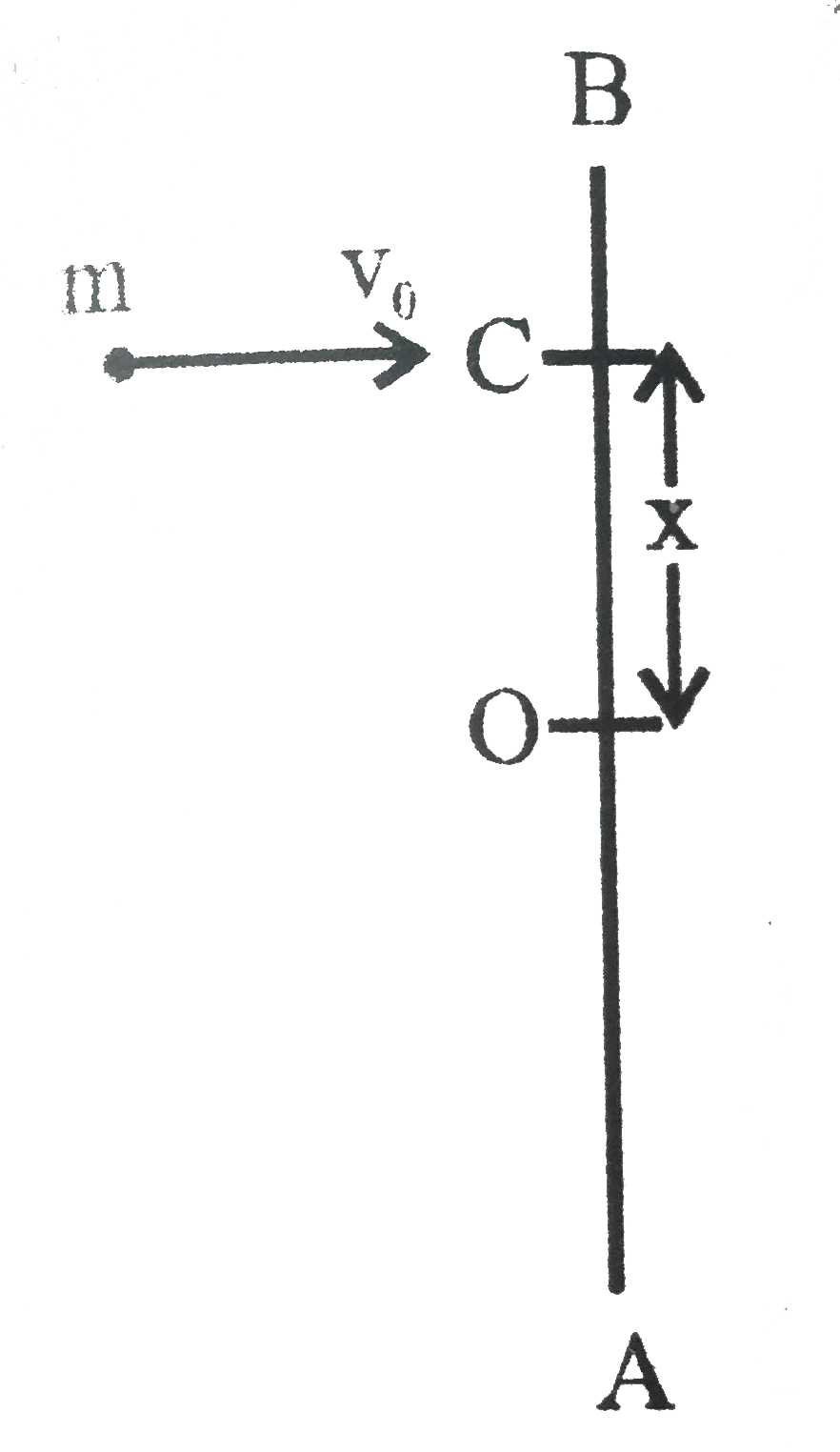 .
.
View SolutionOn a smooth horizontal plane, a rod PQ of length 6m and mass 2kg is placed. The centre of the rod is placed at the origin of the coordinate axes. An impulse of 4N−S is applied at P perependicular to the length of the rod. Find the distance of a point form centre of the rod which is at rest after the impact (in metres)
View Solution
Knowledge Check
A particle at rest is constrained to move on a smooth horizontal surface. Another identical particle hits the stationary particle with a velocity v at an angle θ=60∘ with horizontal. If the particles move together, the velocity of the combination just after the impact is equal to
AvBv/2C√3v/4Dv/4A rod AB of length 2 m and mass 2 kg is lying on a smooth horizontal x-y plane with its centre at origin O as shown in figure. An impulse J of magnitude 10 N-s is applied perpendicular to AB at A.

The distance of point P from centre of the rod which is at rest just after impact isA23 mB13 mC12 mD14m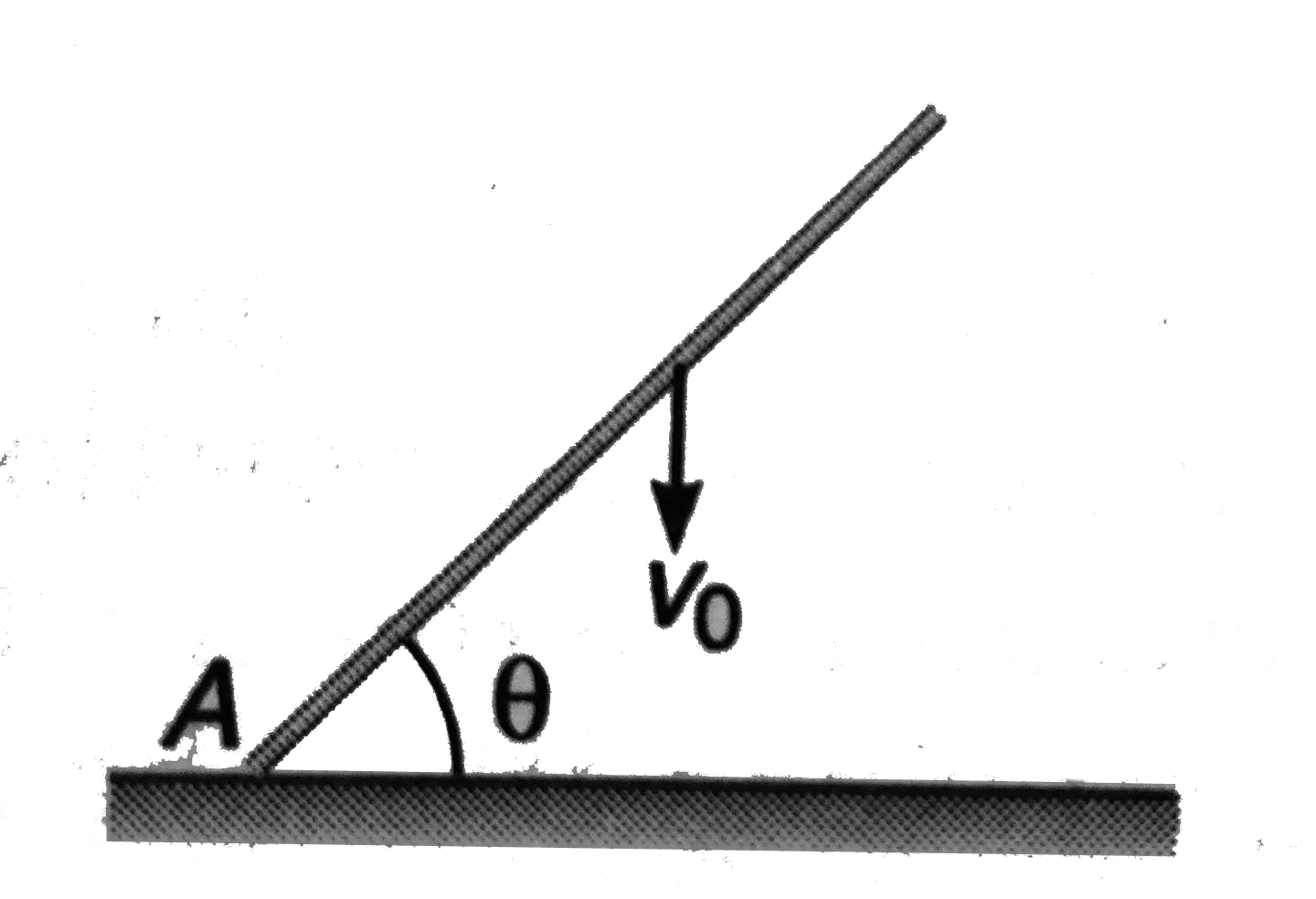
A rod of length l forming an angle θ with the horizontal strikes a frictionless floor at A with its centre of mass velocity v0 and no angular velocity. Assuming that the impact at A is perfectly elastic. Find the angular velocity of the rod immediately after the impact.A3vcosθ2lB12vcosθl(1+cos2)θC12vcosθl(1+3cos2θ)Dvcosθl(1+cos2θ)
A collar B of mass m is at rest and when it is in the position shown, the spring is unstretched. If another collar A of mass mn strikes it so that B slides a distance 4m on the smooth rod before momentarily stopping, determine the velocity of A just after the impact. The coefficient of restitution is e. The spring constant is k.
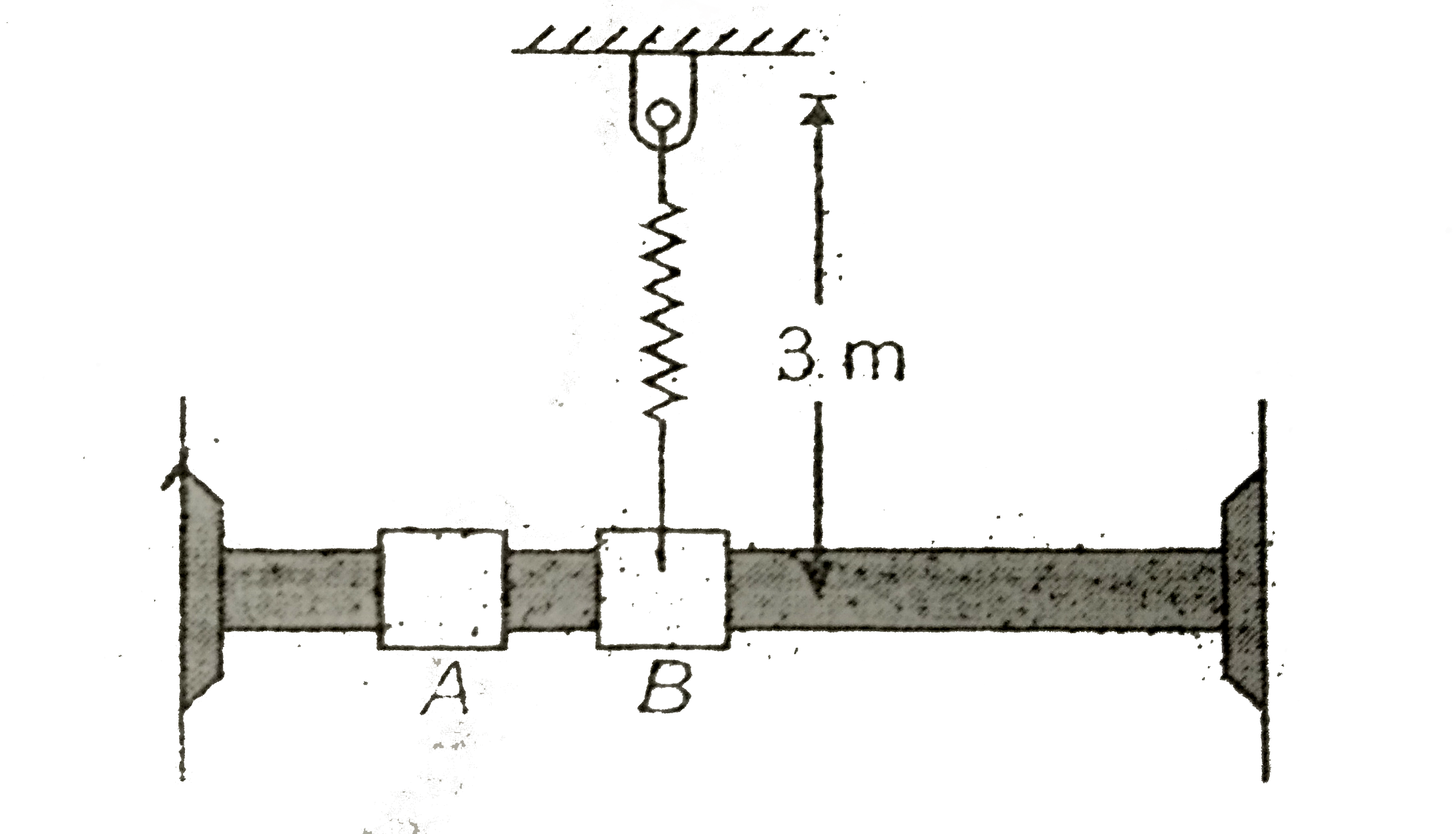
View SolutionA homogenous rod of length l=ηx and mass M is lying on a smooth horizontal floor. A bullet of mass m hits the rod at a distance x from the middle of the rod at a velocity v0 perpendicular to the rod and comes to rest after collision. If the velocity of the farther end of the rod just after the impact is in the opposite direction of v0, then:
View SolutionA homogenous rod of length l=ηx and mass M is lying on a smooth horizontal floor. A bullet of mass m hits the rod at a distance x from the middle of the rod at a velocity v0 perpendicular to the rod and comes to rest after collision. If the velocity of the farther end of the rod just after the impact is in the opposite direction of v0 then:
View SolutionA rod lying on a frictionless horizontal surface is initially given an anglular velocity ω about vertical axis which passes through center of mass. The centre of mass is at rest but not fixed. The length of the rod is L. Subsequently, end A of the rod collides with nail P, which is near to A such that end A becomes stationery immediately after impact. Velocity of end B just after collision will be
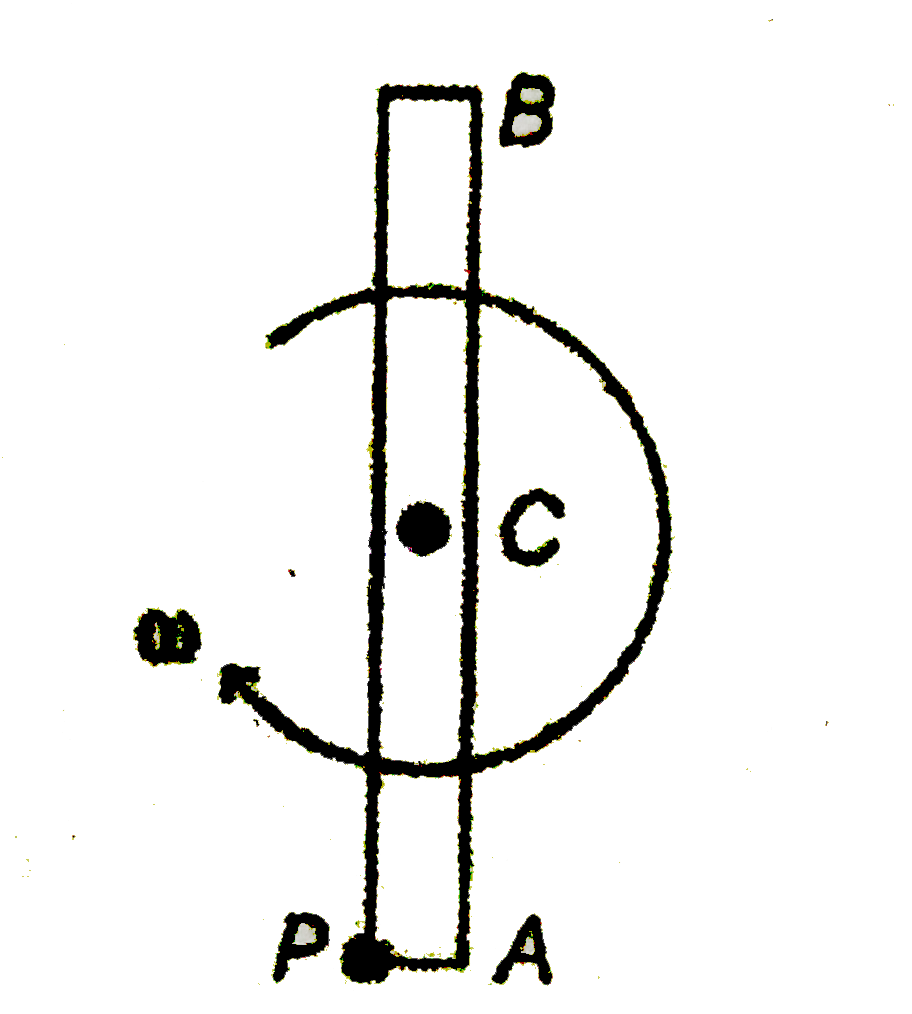
View SolutionA uniform rod of length l and mass 2m rests on a smooth horizontal table. A point mass m moving horizontally at right angles to the rod with initial velocity v collides with one end of the rod and sticks to it.
Determine the position of the point on the rod which remains stationary immediately after collision.
View Solution

