A rod lying on a frictionless horizontal surface is initially given an anglular velocity ω about vertical axis which passes through center of mass. The centre of mass is at rest but not fixed. The length of the rod is L. Subsequently, end A of the rod collides with nail P, which is near to A such that end A becomes stationery immediately after impact. Velocity of end B just after collision will be
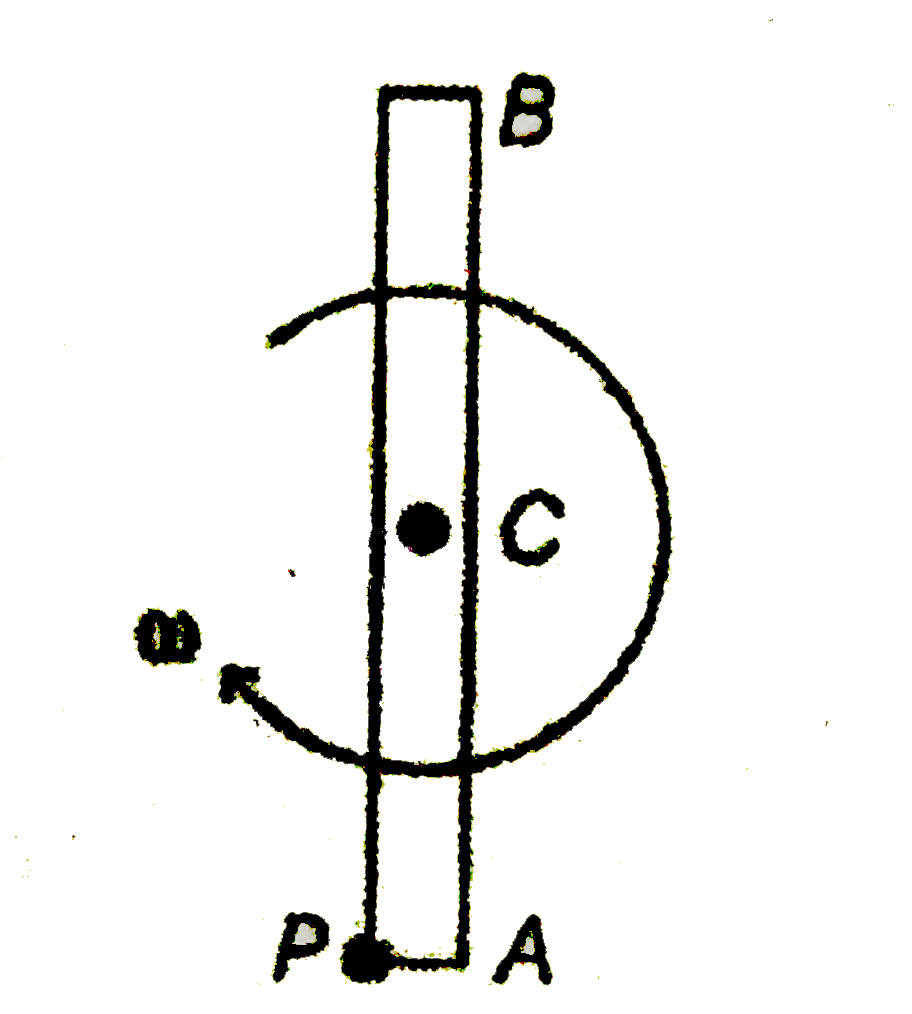
ωL
ωL/2
ωL/4
ωL/6
The correct Answer is:C
Step by step video, text & image solution for A rod lying on a frictionless horizontal surface is initially given an anglular velocity omega about vertical axis which passes through center of mass. The centre of mass is at rest but not fixed. The length of the rod is L. Subsequently, end A of the rod collides with nail P, which is near to A such that end A becomes stationery immediately after impact. Velocity of end B just after collision will be by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- ROTATIONAL MOTIONBook:DC PANDEYChapter:ROTATIONAL MOTIONExercise:More than one option is correct
Explore 36 Videos
- ROTATIONAL MOTIONBook:DC PANDEYChapter:ROTATIONAL MOTIONExercise:Comprehension Type Questions
Explore 41 Videos
- ROTATIONAL MOTIONBook:DC PANDEYChapter:ROTATIONAL MOTIONExercise:Integer Type Questions
Explore 17 Videos
- ROTATIONAL MECHANICSBook:DC PANDEYChapter:ROTATIONAL MECHANICSExercise:Subjective Questions
Explore 2 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBook:DC PANDEYChapter:SEMICONDUCTORS AND ELECTRONIC DEVICESExercise:More than One Option is Correct
Explore 3 Videos
Similar Questions
A thin uniform copper rod of length l and mass m rotates uniformly with an angular velocity ω in a horizontal plane about a vertical axis passing through one of its ends. Determine the tension in the rod as a function of the distance r from the rotation axis. Find the elongation of the rod.
View SolutionA uniform rod of length l is spinning with an angular velocity ω=2vl while its centre of mass moves with a velocity v. Find the velocity of the end of the rod.

View Solution
Knowledge Check
A uniform rod of mass m and length l rotates in a horizontal plane with an angular velocity ω about a vertical axis passing through one end. The tension in the rod at a distance x from the axis is
A12mω2xB12mω2(1−x2l)C12mω2l(1−x2l2)D12mω2l[1−xl]A thin uniform copper rod of length l and cross-section area A and mass m rotates uniformly with an angular velocity ω in a horizontal plane about a vertical axis passing through one of its ends. The elongation of the rod will be
Amω2l26AYBmω2l23AYCmω2l2AYDmω2l22AYA thin uniform rod of mass m and length L rotates with the constant angular velocity ω about .the vertical axis passing through the rod's suspensjon point O. It describes a carried surface, then:
Acentrifugal force acting on rod is mL2sinθω2 and will pass through centre of massBcentrifugal force acting on rod is mL2sinθω2 and will not pass through centre of massCθ=cos−1(3g2ω2L)Dθ=cos−1(gω2L)
A rod AB of length L and mass M is free to move on a frictionless horizontal surface . It is moving with a velocity v , as shown in figure. End B of rod AB strikes the end of the wall. Assuming elastic impact , the angular velocity of the rod AB , just after
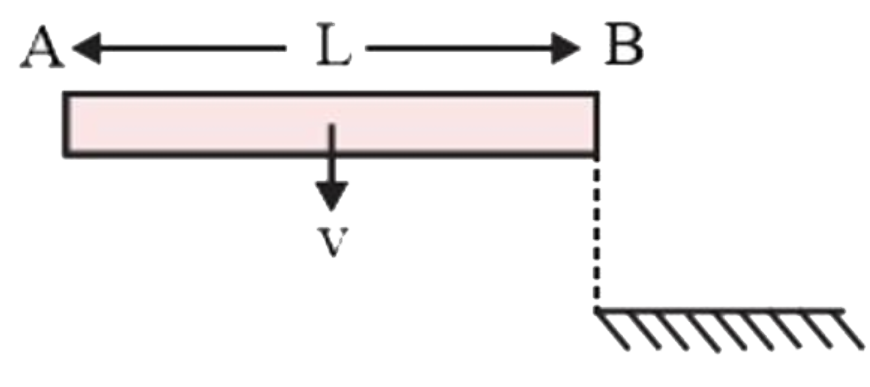
View SolutionA uniform rod of mass m and length l is rotating with constant angular velocity ω about an axis which passes thorugh its one end and perpendicular to the length of rod. The area of cross section of the rod is A and its Young's modulus is y. Neglect gravity. The strain at the mid point of the rod is:
View SolutionA thin rod AB of mass M and length L is rotating with angular speed ω0 about vertically axis passing through its ends B on a horizontal smooth table as shown. If at some instant the hinge at end B of rod is opened then which of the following statemtents is / are correct about motion of rod?

View SolutionA rod AB of length L and mass M is free to move on a frictionless horizontal surface. It is moving with a velocity v, as shown in figure. End B of rod AB strikes the end of the wall. Assuming elastic impact, the angular velocity of the rod AB, just after impact, is
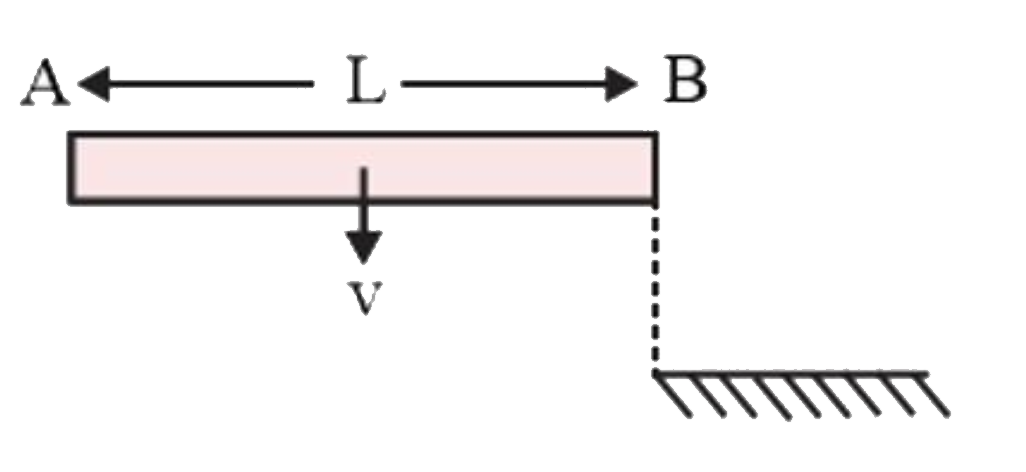
View SolutionA rod length L is held vertically on a smooth horizontal surface. The top end of the rod is given a gentle push. At a certain instant of time, when the rod makes an angle θ with horizontal the velocity of COM of the rod is v0. The velocity of the end of the rod in contact with the surface at that instant is:
View Solution

