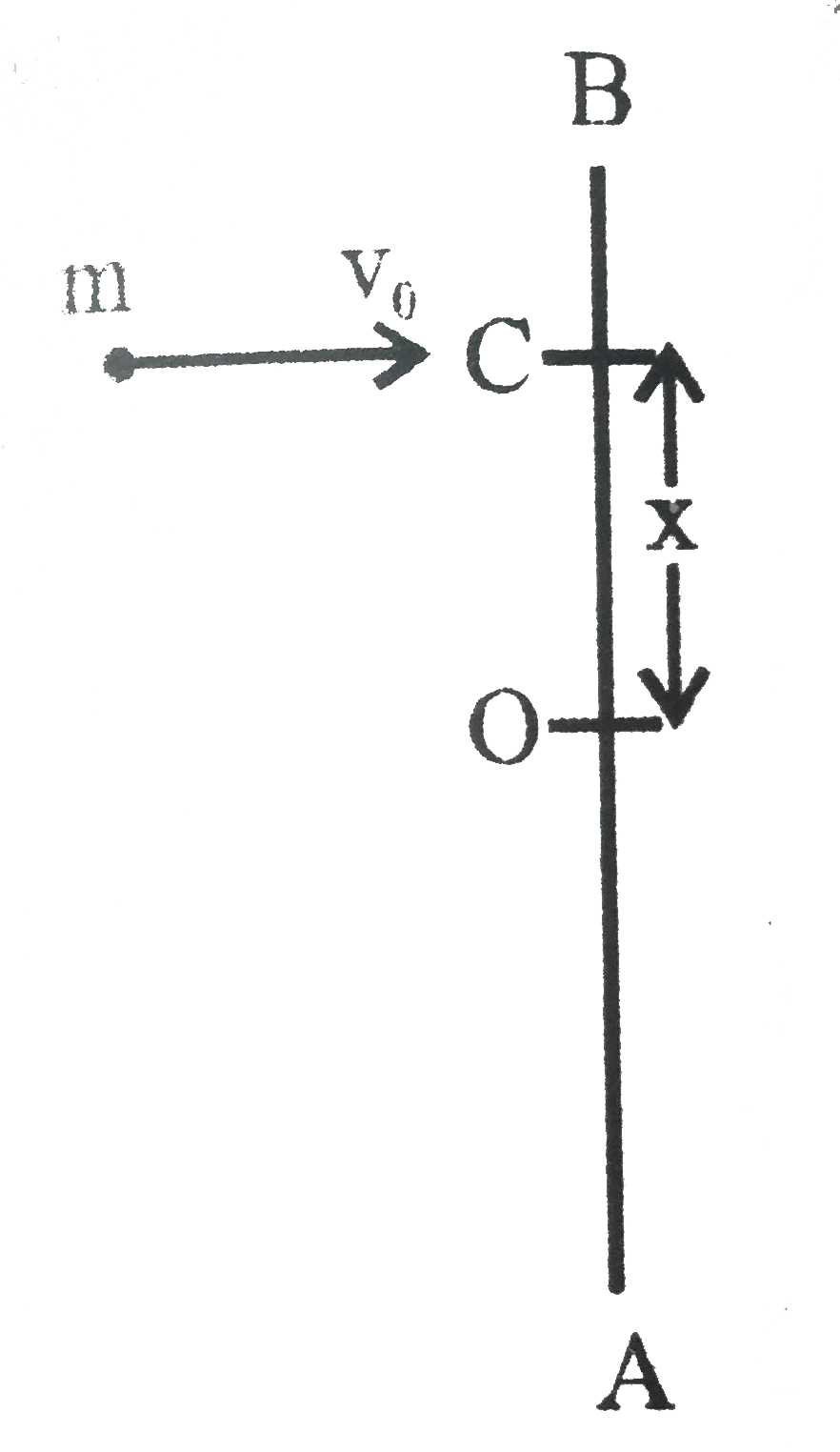
A uniform rod AB of length L and mass M is lying on a smooth table. A small particle if mass m strike the rod with velocity v0 at point C at a distance comes to rest after collision. Then find the value of x, so that point A of the rod remains stationary just after collision.
 .
.
The correct Answer is:L/6
Rod will have translational as well as rotational motion about centre of mass
from conservation of linear momentum
mvo=MVCM …(1)
from conservation of angular momentum about C.M.
Mv_(o)=ML212ω
ω=(mvox)12ML2 ...(2)
for point A to be at rest
VCM=L2ω ...(3)
from (1),(2) & (3)
mvoM=L2×(mvox)12ML2⇒x=L6.
 .
.
Similar Questions
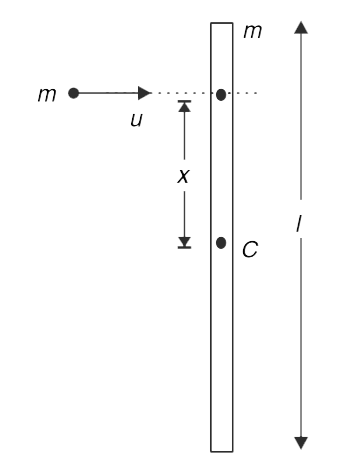
A uniform rod of mass m and length l has been placed on a smooth table A particle of mass m, travelling perpendicular to the rod, hits it at a distance x=l√6 from the centre C of the rod. Collision is elastic.
(a) Find the speed of the centre of the rod and the particle after the collision.
(b) Do you think there is a chance of second Collision? If yes, how is the system of particle and stick moving after the second collision?
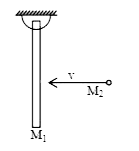
View SolutionA uniform rod of mass M1 is hinged at its upper end. A particle of mass M2 moving horizontally strikes the rod at its mid point elastically. If the particle comes to rest after collision, the value of M1M2 is -
View Solution
Knowledge Check
A uniform rod of mass M is hinged at its upper end. A particle of mass m moving horizontally strikes the rod at its mid point elastically. If the particle comes to rest after collision find the value of M/m?
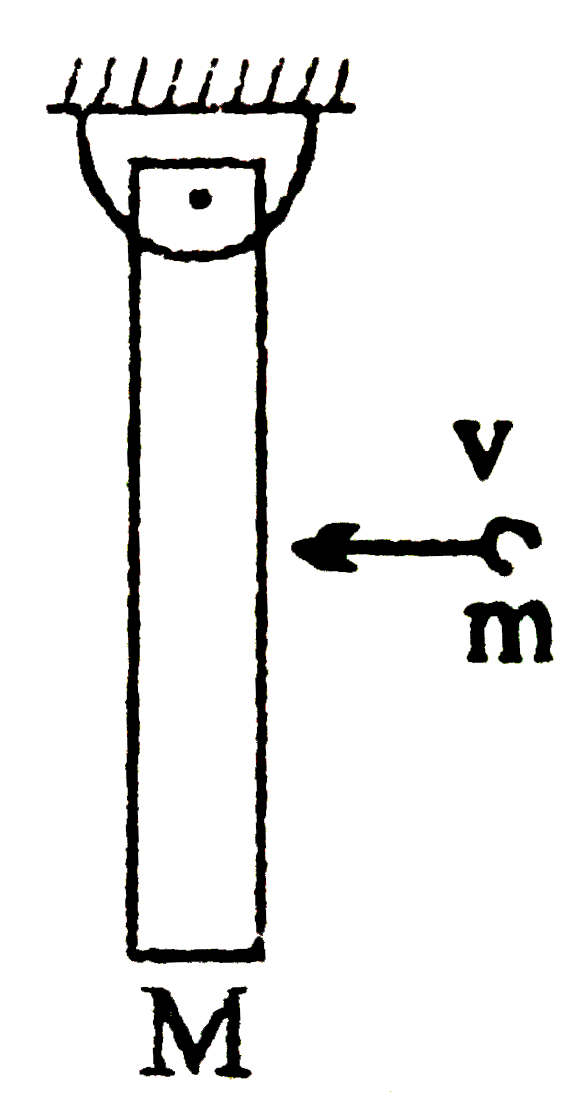 A3/4B4/3C2/3DNone of these
A3/4B4/3C2/3DNone of theseA homogenous rod of length l=ηx and mass M is lying on a smooth horizontal floor. A bullet of mass m hits the rod at a distance x from the middle of the rod at a velocity v0 perpendicular to the rod and comes to rest after collision. If the velocity of the farther end of the rod just after the impact is in the opposite direction of v0, then:
Aη>3Bη<3Cη>2Dη<6A homogenous rod of length l=ηx and mass M is lying on a smooth horizontal floor. A bullet of mass m hits the rod at a distance x from the middle of the rod at a velocity v0 perpendicular to the rod and comes to rest after collision. If the velocity of the farther end of the rod just after the impact is in the opposite direction of v0 then:
Aη>3Bη<3Cη>6Dη<6
A rod of mass m and length l in placed on a smooth table. An another particle of same mass m strikes the rod with velocity v0 in a direction perpendicular to the rod at distance x(<l/2) from its centre . Particle sticks to the end. Let ω be the angular speed of system after collision , then
Find the maximum possible value of impulse (by varying x) that can be imparted to the particle during collision. Particle still sticks to the rod.
View SolutionA uniform rod of length l and mass 2 m rests on a smooth horizontal table. A point mass m moving horizontally at right angles to the rod with velocity v collides with one end of the rod and sticks it. Then
View SolutionA linear impulse ∫Fdt acts at a point C of the smooth rod AB. The value of x is so that the end A remains stationary just after the impact is

View SolutionA rod of mass m and length l in placed on a smooth table. An another particle of same mass m strikes the rod with velocity v0 in a direction perpendicular to the rod at distance x(<l/2) from its centre . Particle sticks to the end. Let ω be the angular speed of system after collision , then
As x is increased from 0 to l/2 , the angular speed ω.
View SolutionA uniform rod of length l and mass 2m rests on a smooth horizontal table. A point mass m moving horizontally at right angles to the rod with initial velocity v collides with one end of the rod and sticks to it.
Determine the position of the point on the rod which remains stationary immediately after collision.
View Solution

