A uniform rod of mass m and length l has been placed on a smooth table A particle of mass m, travelling perpendicular to the rod, hits it at a distance x=l√6 from the centre C of the rod. Collision is elastic.
(a) Find the speed of the centre of the rod and the particle after the collision.
(b) Do you think there is a chance of second Collision? If yes, how is the system of particle and stick moving after the second collision?
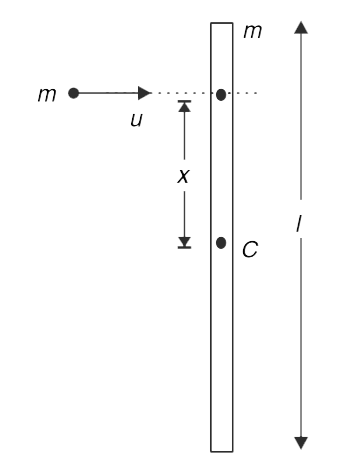
The correct Answer is:Both have speed u2
(b) The stick is at rest. Particle moves in original direction with speed.
Step by step video, text & image solution for A uniform rod of mass m and length l has been placed on a smooth table A particle of mass m, travelling perpendicular to the rod, hits it at a distance x = (l)/(sqrt6) from the centre C of the rod. Collision is elastic. (a) Find the speed of the centre of the rod and the particle after the collision. (b) Do you think there is a chance of second Collision? If yes, how is the system of particle and stick moving after the second collision? by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A uniform rod of mass M and length a lies on a smooth horizontal plane. A particle of mass m moving at a speed v perpendicular to the length of the rod strikes it at a distance a4 from the centre and stops after the collision. Find a. the velocity of the cente of the rod and b. the angular velocity of the rod abut its centre just after the collision.
View SolutionA uniform rod of mass 2 kg and length 1 m lies on a smooth horizontal plane. A particle of mass 1 kg moving at a speed of 2m/s perependicular to the length of the rod strikes it at a distance 14 m from the centre and stops . Find the angular velocity of the rod about its centre just after the collision (in rad/s)
View Solution
Knowledge Check
A uniform rod of mass m, length l rests on a smooth horizontal surface. Rod is given a sharp horizontal impulse p perpendicular to the rod at a distance l/4 from the centre. The angular velocity of the rod will be
A3pmlBpmlCp2mlD2pmlA uniform rod of mass 2 kg and length 1 m lies on a smooth horizontal plane. A particle of mass 1 kg moving at a speed of 2ms−1 perpendicular to the length of the rod strikes it at a distance 14m from the centre and stops. What is the angular velocity of the rod about its centre just after the collision ?
A3rads−1B4rads−1C1rads−1D2rads−1A uniform smooth rod (mass m and length l) placed on a smooth horizontal floor is it by a particle (mass m) moving on the floor, at a distance l4 from one end elastically (e=1). The distance travelled by the centre of the rod after the collision when it has completed three revolutions will be
A2πlBcannot be determinedCπlDnone of the above
A uniform rod of mass M and length L lies on a smooth horizontal plane. A particle of mass m moving at a speed v perpendicular to the length of the rod strikes it at a distance L/6 from the center and stops after the collision. Find
(a) the velocity of center of mass of rod and
(b) the angular velocity of the rod about its center just after collision.
View SolutionA uniform rod of mass m and length l is lying on a smooth table. An impulse J acts on the rod momentarily as shown in figure at point R. Just after that:
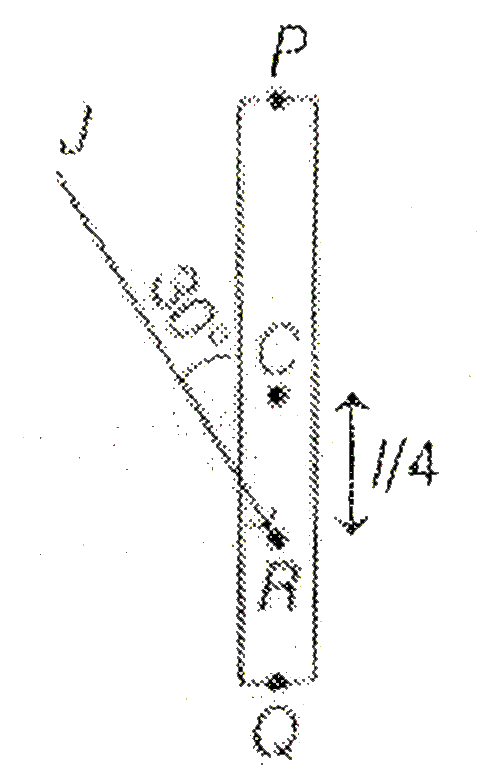
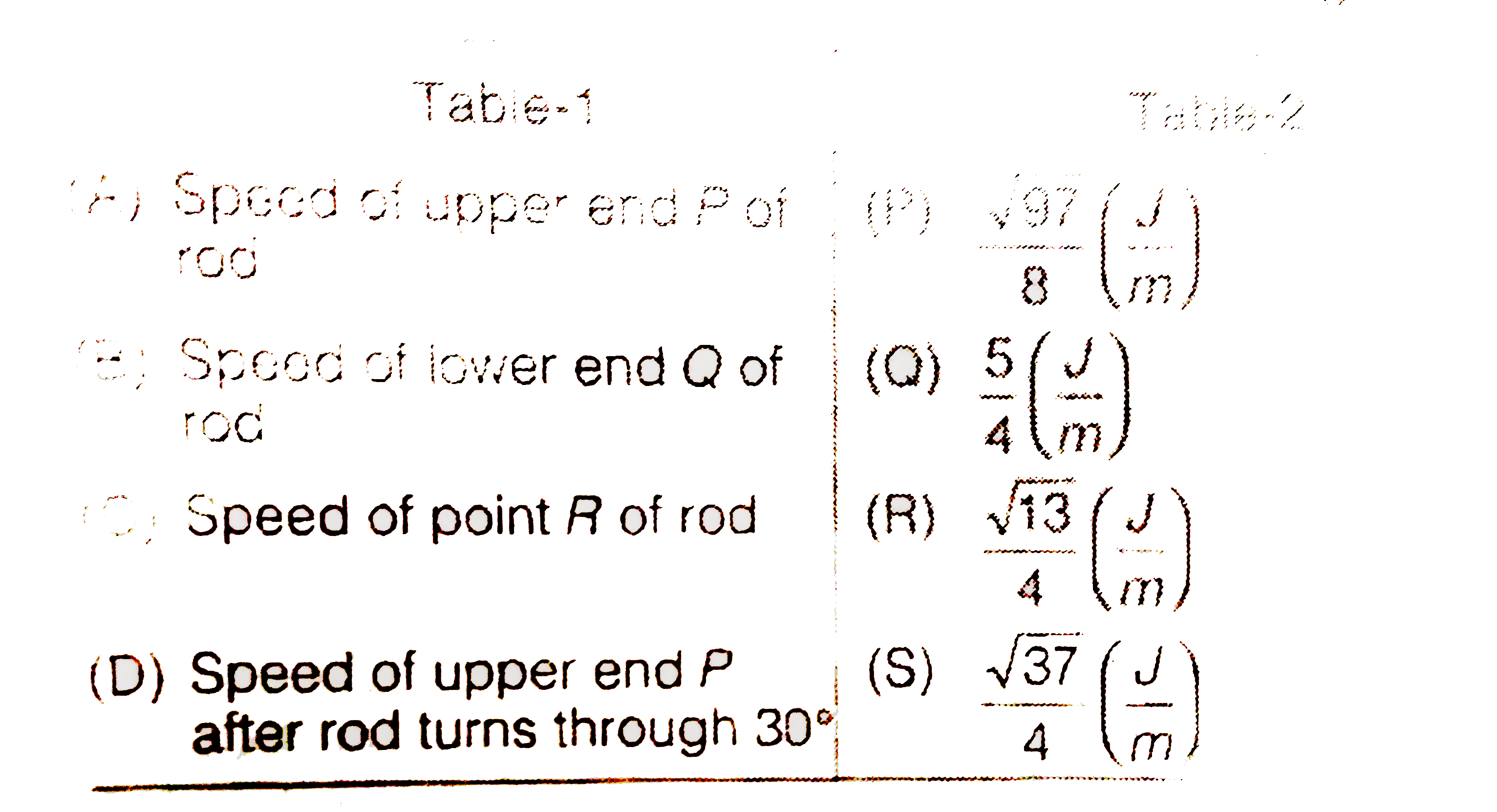
View SolutionA uniform rod AB of mass m and length l is at rest on a smooth horizontal surface. An impulse J is applied to the end B perpendicular to the rod in horizontal direction. Speed of the point A of the rod after giving impulse is:
View SolutionA rod of mass m and length L is kept on a frictionless horizontal floor. A particle of same mass m moving perpendicular to the rod with a speed v strikes at the end of the rod. If coefficient of elasticity for the collision is 1 then calculate angular velocity acquired by the rod.
View SolutionA rod of mass M and length L is kept on a frictionless horizontal floor. A particle of mass m moving perpendicular to the rod with a speed v strikes at the end of the rod and sticks there. Calculate angular velocity acquired by the combined system.
View Solution
