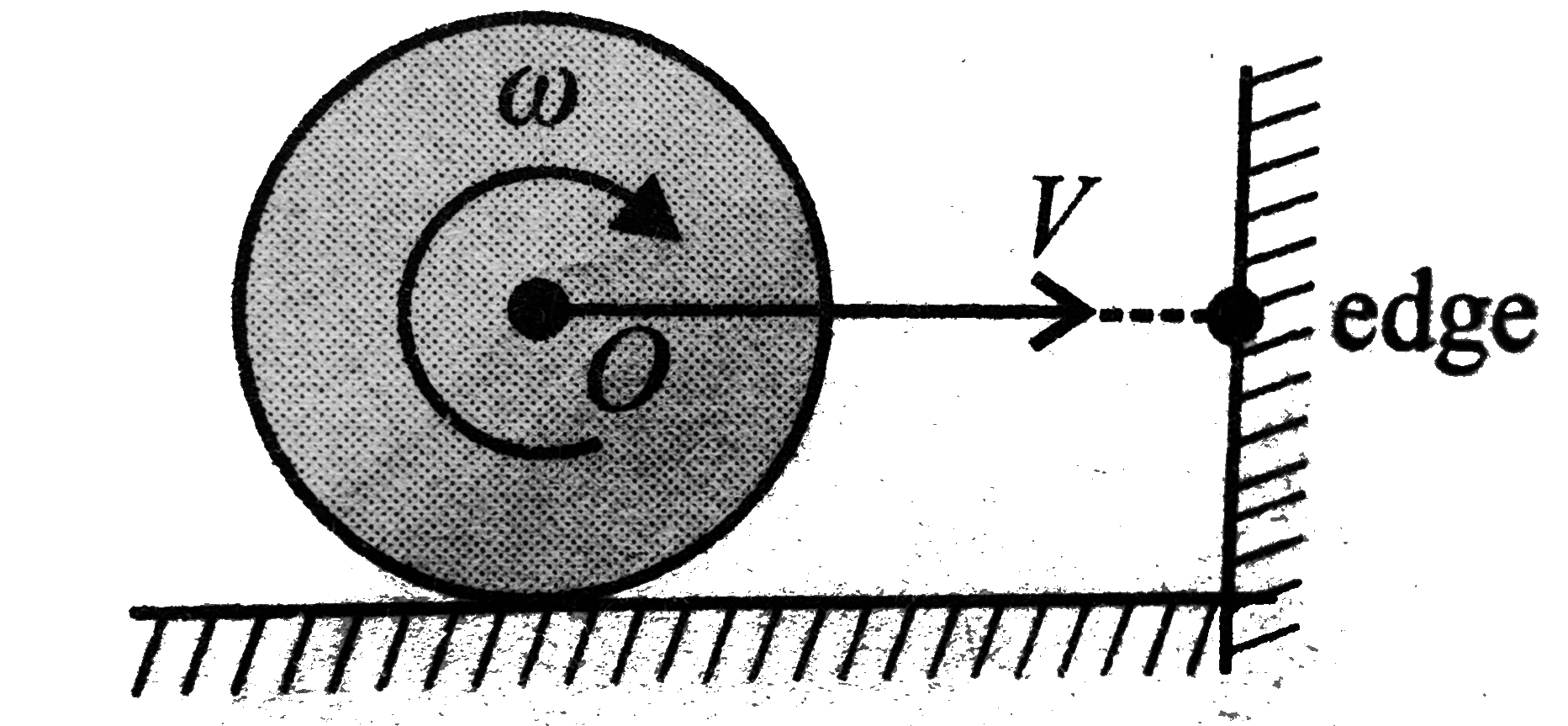
A uniform solid sphere of radius r is rolling on a smooth horizontal surface with velocity v and angular velocity ω=(v=ωr). The sphere collides with a sharp edge on the wall as shown in figure. The coefficient of friction between the sphere and the edge μ=1/5. Just after the collision the angular velocity of the sphere becomes equal to zero. The linear velocity of the surface just after the collision is equal to

V
V5
3v5
2V5
The correct Answer is:A
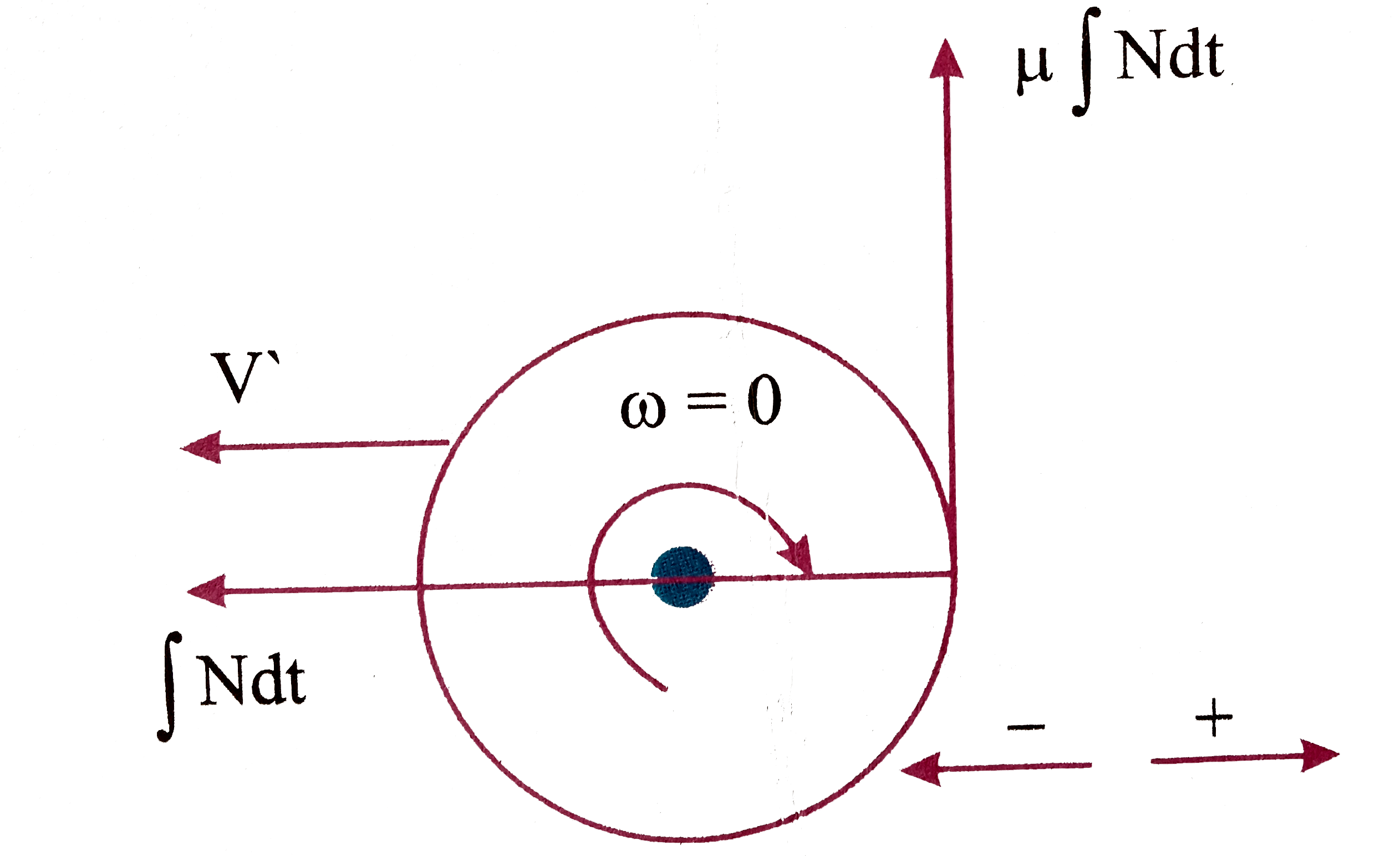
∫Ndt
−∫Ndt=−mV'−(mV)......(1)
μR∫Ndt=25mR2(VR)......(2)
From eqns,. (1)and (2), we get
∫Ndt=2mV and V'=V
Topper's Solved these Questions
- SYSTEM OF PARTICLESBOOK - NARAYNACHAPTER - SYSTEM OF PARTICLESEXERCISE - Level-V
72 Videos
- PHYSICAL WORLDBOOK - NARAYNACHAPTER - PHYSICAL WORLDEXERCISE - C.U.Q
10 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION BOOK - NARAYNACHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTION EXERCISE - EXERCISE - IV
39 Videos
Similar Questions
A disc of radius R is moving on a rough horizontal surface with velocity v and angular speed ω at an instant as shown in figure. Choose the correct statement.

View SolutionA uniform solid sphere of radius R, rolling without sliding on a horizontal surface with an angular velocity ω0, meets a rough inclined plane of inclination θ=60∘. The sphere starts pure rolling up the plane with an angular velocity ω Find the value of ω.

View Solution
Knowledge Check
A uniform solid sphere of radius r is rolling on a smooth horizontal surface with velocity V and angular velocity ω=(V=ωr). The sphere collides with a sharp edge on the wall as shown in Fig. The coefficient of friction between the sphere and the edge μ=1/5. Just after the collision the angular velocity of the sphere becomes equal to zero. The linear velocity of the sphere just after the collision is equal to
 AVBV5C3V5DV6
AVBV5C3V5DV6Relation between Linear velocity (v) and Angular velocity (ω)
Av=rωBω=vωCr=vωDv=ωrA sphere of radius R is rolling on a rough horizontal surface. The magnitude of velocity of A with respect to ground will be
 A√2vCMB2VCMsinθC√2vCM√1+sinθDNo sufficient information
A√2vCMB2VCMsinθC√2vCM√1+sinθDNo sufficient information
A sphere is performing pure rolling on a rough horizontal surface with constant angular velocity. Frictional force acting on the sphere is zero.
Velocity of contact point is zero.
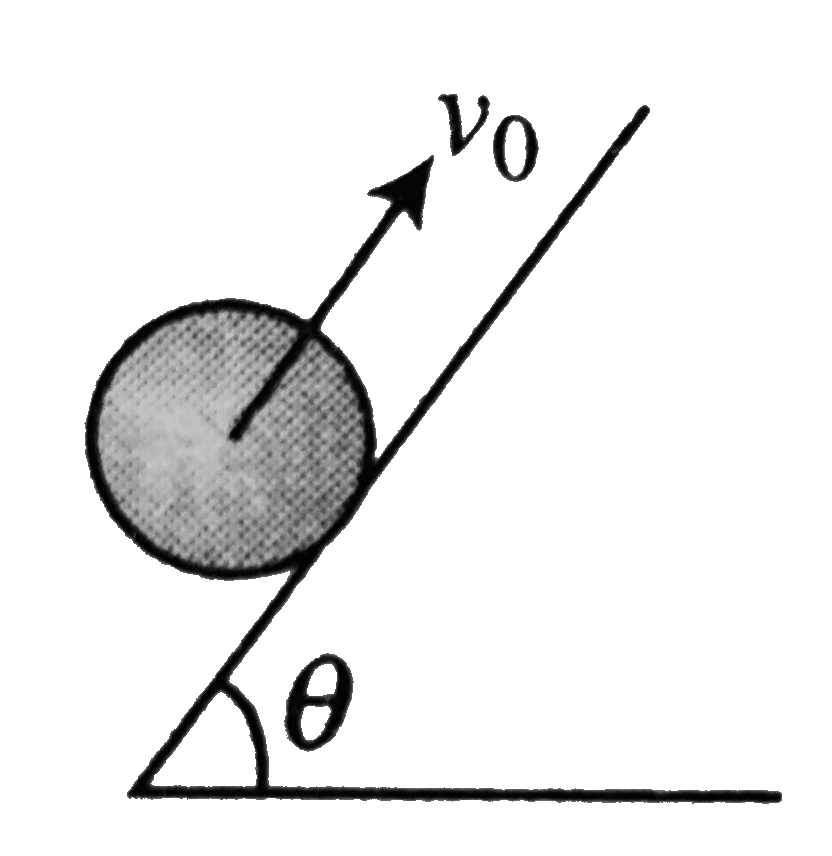
View SolutionA sphere is projected up an inclined plane with a velocity v0 and zero angular velocity as shown. The coefficient of friction between the sphere and the plane is μ=tanθ.. Find the total time of rise of the sphere.
View SolutionA uniform circular disc of radius r is placed on a rough horizontal surface and given a linear velocity v0 and angular velocity ω0 as shown. The disc comes to rest after moving some distance to the right. It follows that

View SolutionA uniform circular ring of radius R is first rotated about its horizontal axis with an angular velocity ω0 and then carefully placed on a rough horizontal surface as shown. The coefficient of friction between the surface and the rings μ. Time after which its angular speed is reduced to 0.5ω0 is

View SolutionA long horizontal plank of mass m is lying on a smooth horizontal surface. A sphere of same mass m and radius r is spinned about its own axis with angular velocity we and gently placed on the plank. The coefficient of friction between the plank and the sphere is μ. After some time the pure rolling of the sphere on the plank will start. Answer the following questions.

Find the velocity of the sphere after the pure rolling starts
View Solution
