A sphere is performing pure rolling on a rough horizontal surface with constant angular velocity. Frictional force acting on the sphere is zero.
Velocity of contact point is zero.
Statement-1 is True, Statement-2 is Ture , Statement -2 is a correct explanation for statement -1.
Statement-1 is True, Statement-2 is True , Statement-2 is NOT a correct explanation fro Statement -1.
Statement-1 is True, Statement-2 is False.
Statement-1 is False, Statement-2 is True.
The correct Answer is:B
If angular velocity is constant then frictional force acting on sphere is zero. In case of pure rolling velocity of contact point is zero.
Similar Questions
Knowledge Check
A disc is performing pure rolling on a smooth stationary surface with constant angular velocity as shown in Fig,. At any instant, for the lower most point of the disc,
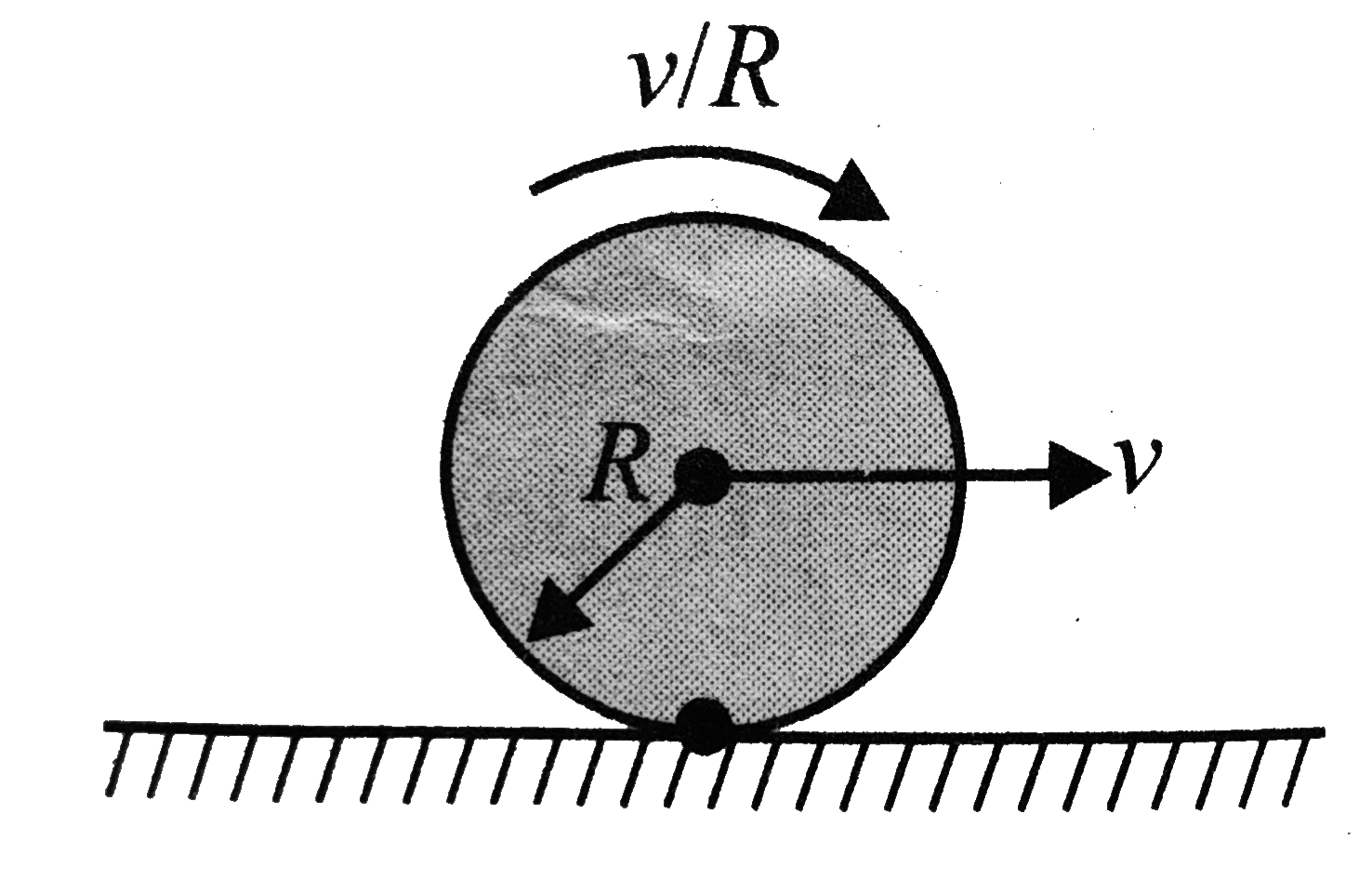 Avelocity is v, acceleration is zeroBvelocity is zero, acceleration is zeroCvelocity is v, acceleration is v2/RDvelocity is 0, acceleration is v2/R
Avelocity is v, acceleration is zeroBvelocity is zero, acceleration is zeroCvelocity is v, acceleration is v2/RDvelocity is 0, acceleration is v2/RA disc of radius R is rolling purely on a flat horizontal surface, with a constant angular velocity. The angle between the velocity and acceleration vectors of point P is
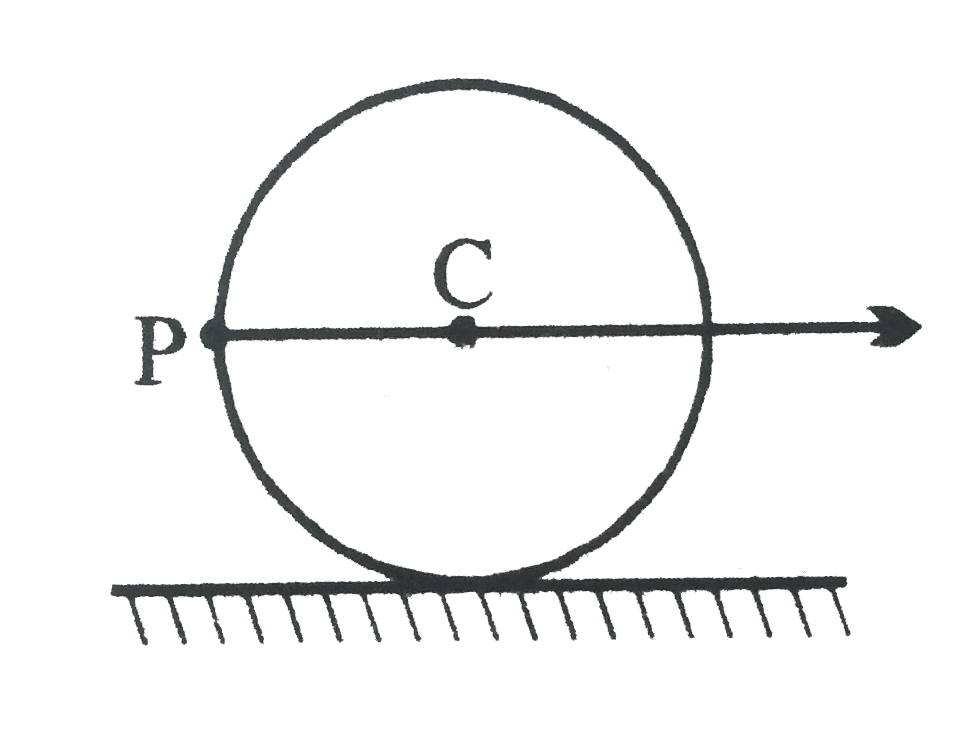 .AzeroB45∘C135∘Dtan−1(1/2)
.AzeroB45∘C135∘Dtan−1(1/2)
A disc of radius R is rolling purely on a flat horizontal surface, with a constant angular velocity the angle between the velocity ad acceleration vectors of point P isAzeroB45∘Ctan−1(2)Dtan−1(1/2)
A sphere of radius R is rolling on a rough horizontal surface. The magnitude of velocity of A with respect to ground will be

View SolutionA sphere rolling on a rough horizontal surface with constant velocity then it start going up on a smooth inclined plane. Rotational KE of sphere decreases continuosly on horizontal and inclined surface.
Rotational KE decreases if torque due to friction opposes angular velocity of sphere.
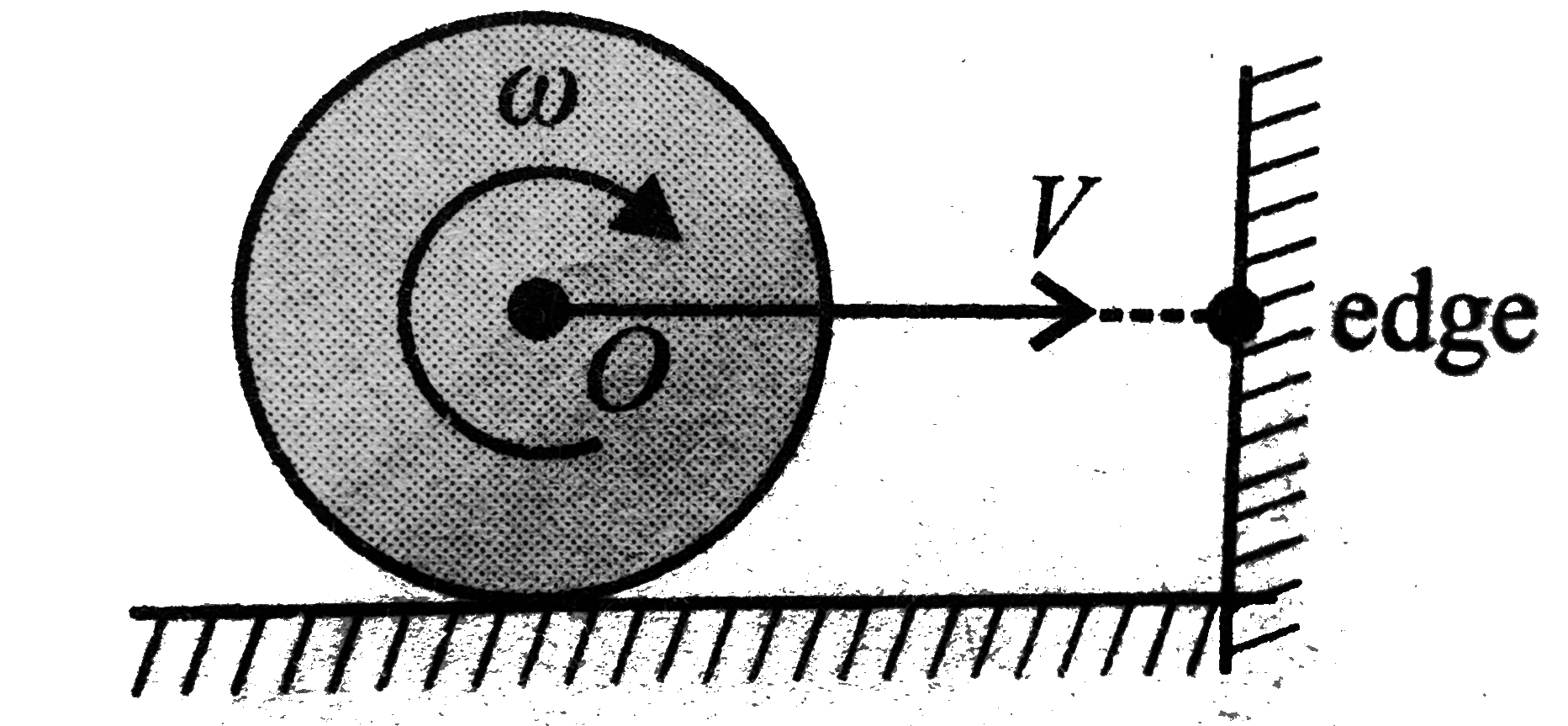
View SolutionA uniform solid sphere of radius r is rolling on a smooth horizontal surface with velocity v and angular velocity ω=(v=ωr). The sphere collides with a sharp edge on the wall as shown in figure. The coefficient of friction between the sphere and the edge μ=1/5. Just after the collision the angular velocity of the sphere becomes equal to zero. The linear velocity of the surface just after the collision is equal to

View SolutionA uniform solid sphere of radius r is rolling on a smooth horizontal surface with velocity V and angular velocity ω=(V=ωr). The sphere collides with a sharp edge on the wall as shown in Fig. The coefficient of friction between the sphere and the edge μ=1/5. Just after the collision the angular velocity of the sphere becomes equal to zero. The linear velocity of the sphere just after the collision is equal to
View SolutionA block is sliding on a rough horizontal surface. If the contact force on the block is √2 times the frictional force, the coefficient of friction is
View Solution
