A block is sliding on a rough horizontal surface. If the contact force on the block is √2 times the frictional force, the coefficient of friction is
0.25
1√2
√2
1
The correct Answer is:D
To solve the problem, we need to find the coefficient of friction (μ) given that the contact force (R) on the block is √2 times the frictional force (F). Here’s a step-by-step solution:
Step 1: Understand the Forces Acting on the Block
The block is sliding on a rough horizontal surface, which means there are two main forces acting on it:
- The normal force (N) acting perpendicular to the surface.
- The frictional force (F) acting opposite to the direction of motion.
Step 2: Relate the Contact Force and Frictional Force
According to the problem, the contact force (R) is given as:
R=√2F
where F is the frictional force.
Step 3: Express the Frictional Force in Terms of the Coefficient of Friction
The frictional force can be expressed as:
F=μN
where μ is the coefficient of friction and N is the normal force.
Step 4: Substitute the Frictional Force into the Contact Force Equation
Substituting F=μN into the equation for R gives:
R=√2(μN)
Thus,
R=√2μN
Step 5: Use the Pythagorean Theorem for the Contact Force
The contact force R can also be expressed using the Pythagorean theorem since the frictional force and normal force are perpendicular:
R=√F2+N2
Substituting F=μN into this equation gives:
R=√(μN)2+N2
R=√μ2N2+N2
R=√N2(μ2+1)
R=N√μ2+1
Step 6: Set the Two Expressions for R Equal to Each Other
Now we have two expressions for R:
1. R=√2μN
2. R=N√μ2+1
Setting them equal gives:
√2μN=N√μ2+1
Step 7: Simplify the Equation
Assuming N≠0, we can divide both sides by N:
√2μ=√μ2+1
Step 8: Square Both Sides
Squaring both sides results in:
2μ2=μ2+1
Step 9: Rearrange the Equation
Rearranging gives:
2μ2−μ2=1
μ2=1
Step 10: Solve for μ
Taking the square root of both sides gives:
μ=1
Thus, the coefficient of friction is:
μ=1
Final Answer
The coefficient of friction (μ) is 1.
---
The block is sliding on a rough horizontal surface, which means there are two main forces acting on it:
- The normal force (N) acting perpendicular to the surface.
- The frictional force (F) acting opposite to the direction of motion.
According to the problem, the contact force (R) is given as:
R=√2F
where F is the frictional force.
The frictional force can be expressed as:
F=μN
where μ is the coefficient of friction and N is the normal force.
Substituting F=μN into the equation for R gives:
R=√2(μN)
Thus,
R=√2μN
The contact force R can also be expressed using the Pythagorean theorem since the frictional force and normal force are perpendicular:
R=√F2+N2
Substituting F=μN into this equation gives:
R=√(μN)2+N2
R=√μ2N2+N2
R=√N2(μ2+1)
R=N√μ2+1
Now we have two expressions for R:
1. R=√2μN
2. R=N√μ2+1
√2μN=N√μ2+1
Assuming N≠0, we can divide both sides by N:
√2μ=√μ2+1
Squaring both sides results in:
2μ2=μ2+1
Rearranging gives:
2μ2−μ2=1
μ2=1
Taking the square root of both sides gives:
μ=1
μ=1
The coefficient of friction (μ) is 1.
Topper's Solved these Questions
Similar Questions
A wooden block of mass M resting on a rough horizontal surface is pulled with a force F at an angle with the horizontal. If is the coefficient of kinetic friction between the block and the surface, then acceleration of the block is -
View SolutionA cubical block of side L rests on a rough horizonta surface with coefficient of friction μ. A horizontal force F is applied on the block as shown. If the coefficient of friction is sufficiently high so that the block does not slide before toppling, the minimum force required to topple the block is

View Solution
Knowledge Check
A block is in limiting equilibrium on a rough horizontal surface. If the net contact force is √3 times the normal force, the coefficient of static friction is
A√2B1√2C0.5D1√3A block of mass m is placed on a rough horizontal surface. If minimum force to pull the block is mg2 then coefficient of friction is :
A12B√3C1√3DNoneA horizontal force of 20 N is applied to a block of 10 kg resting on a rough horizontal surface. How much additional force is required to just move the block, if the coefficient of static friction between the block and the surface is 0.4 ?
A15.5 NB10.3 NC8.5 ND19.2 N
A cubical block of side L rests on a rough horizonta surface with coefficient of friction μ. A horizontal force F is applied on the block as shown. If the coefficient of friction is sufficiently high so that the block does not slide before toppling, the minimum force required to topple the block is

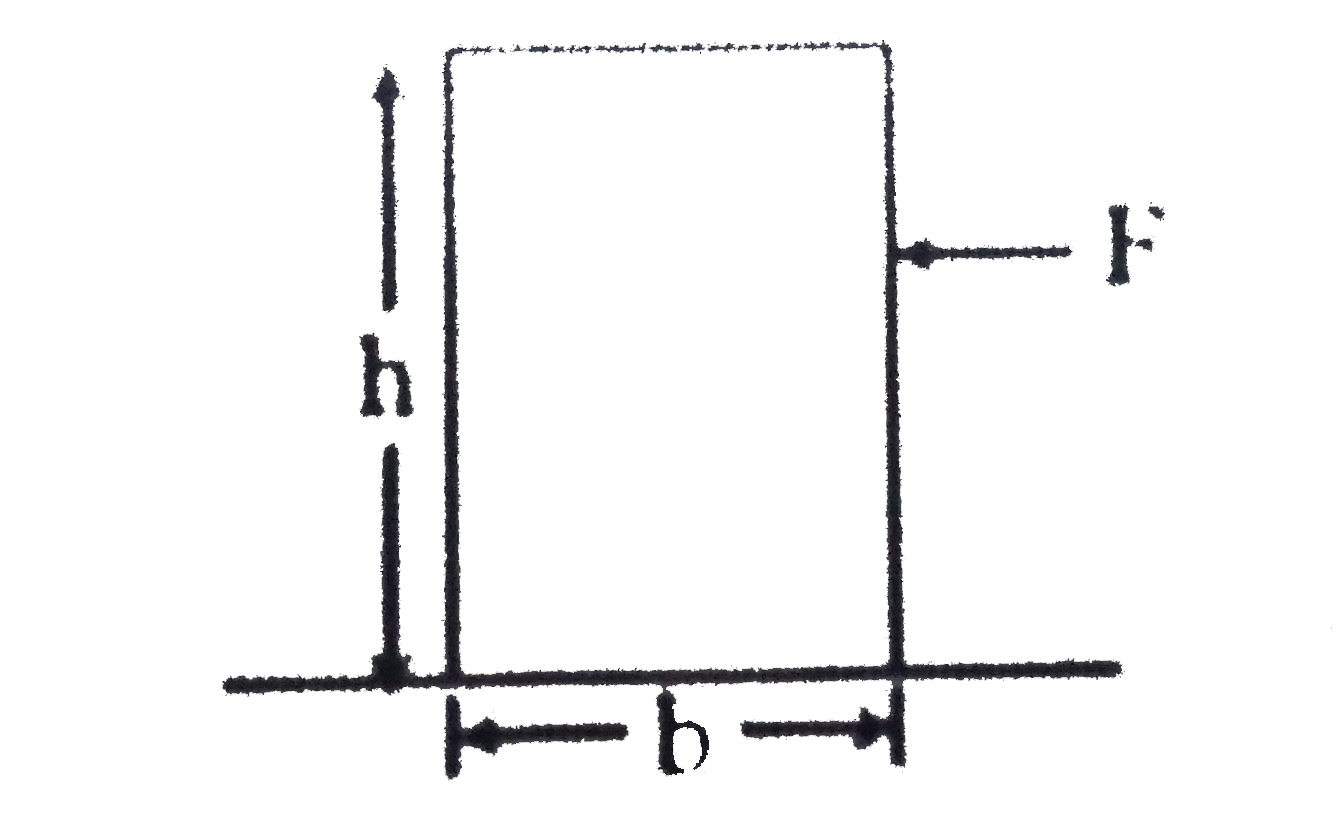
View SolutionA homogenous block of mass m, width b and height h is resting on a rough horizontal surface A horizontal force F is applied to it , which makes it to move with a constant velocity . The coefficient of friction between block and surface is μ Find the greatest height at which force F may be applied to slide the block with out tipping over
View SolutionA block of mass 8 kg is placed on a rough horizontal plane. A time dependent force F=kt2acts on the block, where k=3N/s2. Coefficient of friction is0.6. Force of friction between the block and the plane at t=1s is
View SolutionA block of mass 5kg is on a rough horizontal surface and is at rest. Now a force of 24 N is imparted to it with negligible impulse. If the coefficient of kinetic friction is 0.4 and g=9.8m/s2 , then the acceleration of the block is
View SolutionA cubical block of side L rests on a rough horizontal surface with coefficient of friction μ. A horizontal force F is applied on the block as shown. If the coefficient of frictions sufficienty high so that the block does not slide before toppling, the minimum force required to topple the block is :
 .
.
View Solution