A sphere has to purely roll upwards. At an instant when the velocity of sphere is v, frictional force acting on it is

downwards and μmgcosθ
downwards and 2mgsinθ7
upward and μmgcosθ
upwards and 2mgsinθ7
The correct Answer is:D
In case of rolling in the inclined plane, friction is static and acts in the upward direction and is given by
f=mgsinθ1+R2k2………..i
Form sphere k2=25R2 ……….ii
Form eqn i andii f=27mgsinθ (upwards)
Topper's Solved these Questions
- RIGID BODY DYNAMICS 2Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 2Exercise:Multiple Correct
Explore 26 Videos
- RIGID BODY DYNAMICS 2Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 2Exercise:Linked Comprehension
Explore 71 Videos
- RIGID BODY DYNAMICS 2Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 2Exercise:Subjective
Explore 19 Videos
- RIGID BODY DYNAMICS 1Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 1Exercise:Integer
Explore 11 Videos
- SOUND WAVES AND DOPPLER EFFECTBook:CENGAGE PHYSICSChapter:SOUND WAVES AND DOPPLER EFFECTExercise:Integer
Explore 16 Videos
Similar Questions
A solid sphere of mass M and radius R is pulled by a force F as shown in figure . If the sphere does not slip over the surface , then frictional force acting on the sphere is

View SolutionA solid sphere of mass m and radius R is on a rough surface as shown in figure. Two forces having magnitude 2F and F are applied as shown. If the sphere perfors pure rolling along right direction, then frictional force acting on the sphere is
_PHY_211_Q01.png)
View Solution
Knowledge Check
A disc and a solid sphere of same mass and radius roll down an inclined plane. The ratio of thhe friction force acting on the disc and sphere is
A76B54C32Ddepends on angle of inclinationA sphere is performing pure rolling on a rough horizontal surface with constant angular velocity. Frictional force acting on the sphere is zero.
Velocity of contact point is zero.AStatement-1 is True, Statement-2 is Ture , Statement -2 is a correct explanation for statement -1.BStatement-1 is True, Statement-2 is True , Statement-2 is NOT a correct explanation fro Statement -1.CStatement-1 is True, Statement-2 is False.DStatement-1 is False, Statement-2 is True.A sphere of mass m is rolling without sliding along positive x-axis on a rough horizontal surface of coefficient of friction μ. It elastically collides with a wall and then returns. The correct statement of frictional force (f) acting on the sphere is
Af=μmgˆi before collision and f=μmgˆi after collisionBf=0 before collision and f=+μmgˆi after collisionCf<μmgˆi before collision and f=μmgˆi after collisionDf=μmgˆi before collision and just after collision
The figure shows a smooth inclined plane of inclination θ fixed in a car. A sphere is set in pure rolling on the incline. For what value of the acceleration of the car in the horizontal direction the sphere will continue pure rolling?
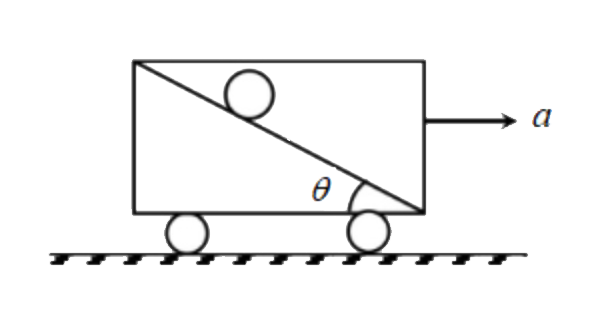
View SolutionFigures shows a smooth inclined plane of inclination θ fixed ina car. A sphere is set in pure rolling on the incline. For what value of a (the acceleration of car in horizontal direction) the sphere will continue pure rolling ?

View Solution
A sphere of mass m and radius r rolls without slipping over a tunnel of width d=8r5 as shown in the figure. (in the figure the sphere rolls perpendicular to the plane of the page) the velocity of centre of mass of sphere is v directed into the plane of the page. the maximum speed of a point on the sphere is
View SolutionState of motion of the sphere at t = 0 is described in figure, Centre of the sphere is moving towards right with a speed u and angular velocity of the sphere is u/2r in the anticlockwise sense. Here is the radius of sphere. We can understand that it is a case of slipping and after some time sphere starts pure rolling due to friction from the surface. We can assume direction towards right as positive and thus clockwise sense should be treated positive for rotational motion. Assume ng coefficient of friction between sphere and the surface. Mass of sphere is m.

What will be the speed of sphere when it starts pure rolling?
View Solution
A solid sphere of mass m and radius R is rolling without slipping on a rough horizontal surface with angular acceleration α. Centre of mass of sphere lies at a distance R√2 from the centre of sphere. Find the normal force applied by sphere on the surface at an instant when line joining centre of mass of sphere and centre of sphere makes an angle 45∘ with the vertical and angular velocity of sphere at this instant is ω.
View Solution

