A uniform sphere of mass m radius r and moment of inertia I about its centre moves along the x-axis as shown in Fig Its centre of mass moves with velocity =v0, and it rotates about its centre of mass with angular velocity =ω0. Let →L=(Iω0+mv0r)(−k). The angular momentum of the body about the origin O is

→L only if v0=ωr
greater than →L, if v0>ω0r
less than →L, if v0>ω0r
→L, for all values of ω0 and v0
The correct Answer is:D
→L=→R×m→v0+I→ω0=mv0+Iω0 (which is constant)

Topper's Solved these Questions
- RIGID BODY DYNAMICS 2Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 2Exercise:Multiple Correct
Explore 26 Videos
- RIGID BODY DYNAMICS 2Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 2Exercise:Linked Comprehension
Explore 71 Videos
- RIGID BODY DYNAMICS 2Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 2Exercise:Subjective
Explore 19 Videos
- RIGID BODY DYNAMICS 1Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 1Exercise:Integer
Explore 11 Videos
- SOUND WAVES AND DOPPLER EFFECTBook:CENGAGE PHYSICSChapter:SOUND WAVES AND DOPPLER EFFECTExercise:Integer
Explore 16 Videos
Similar Questions
A solid sphere of radius r and mass m rotates about an axis passing through its centre with angular velocity ω. Its K.E. Is
View Solution
A rod of mass 2 kg ad length 2 m is rotating about its one end O wth an angular velocity ω=4rad/s. Find angular momentum of the rod about the axis rotation.
View Solution
Knowledge Check
A particle of mass m is moving with constant velocity v parallel to the x-axis as shown in the figure. Its angular momentum about origin O is
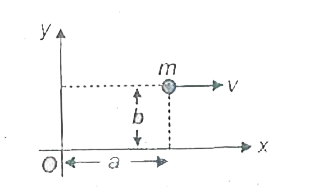 AmvbBmvaCmv√a2+b2Dmv(a+b)
AmvbBmvaCmv√a2+b2Dmv(a+b)A disc of mass m and radius R moves in the x−y plane as shown in Fig. The angular momentum of the disc about the origin O at the instant shown is
 A−52mR2ωˆkB73mR2ωˆkC−92mR2ωˆkD52mR2ωˆk
A−52mR2ωˆkB73mR2ωˆkC−92mR2ωˆkD52mR2ωˆkA solid aluminimum sphere of radius R has moment of inertia I about an axis through its centre. The moment of inertia about a central axis of a solid aluminimum sphere of radius 2R is.
A4 IB8 IC16 ID32 I
A solid cylinder of mass 20kg rotates about its axis with angular velocity of 100 radian s−1. The radius of the cylinder is 0.25m. The magnitude of the angular momentum of the cylinder about its axis of rotation is
View SolutionA ring of mass m and radius R is given a charge q. It is then rotated about its axis with angular velocity ω.Find
(iii)Magnetic moment of ring.
View SolutionA thin uniformring of radius R carrying uniform charge Q and mass M rotates about its axis with angular velocity ω. The ratio of its magnetic moment and angular momentum is:
View SolutionA ring of mass m and radius R is being rotated about its axis with angular velocity ω. If a increases then tension in ring
View SolutionThe moment of inertia of a cylinder of radius R, length L and mass M about an axis passing through its centre of mass and normal to its length is
View Solution

