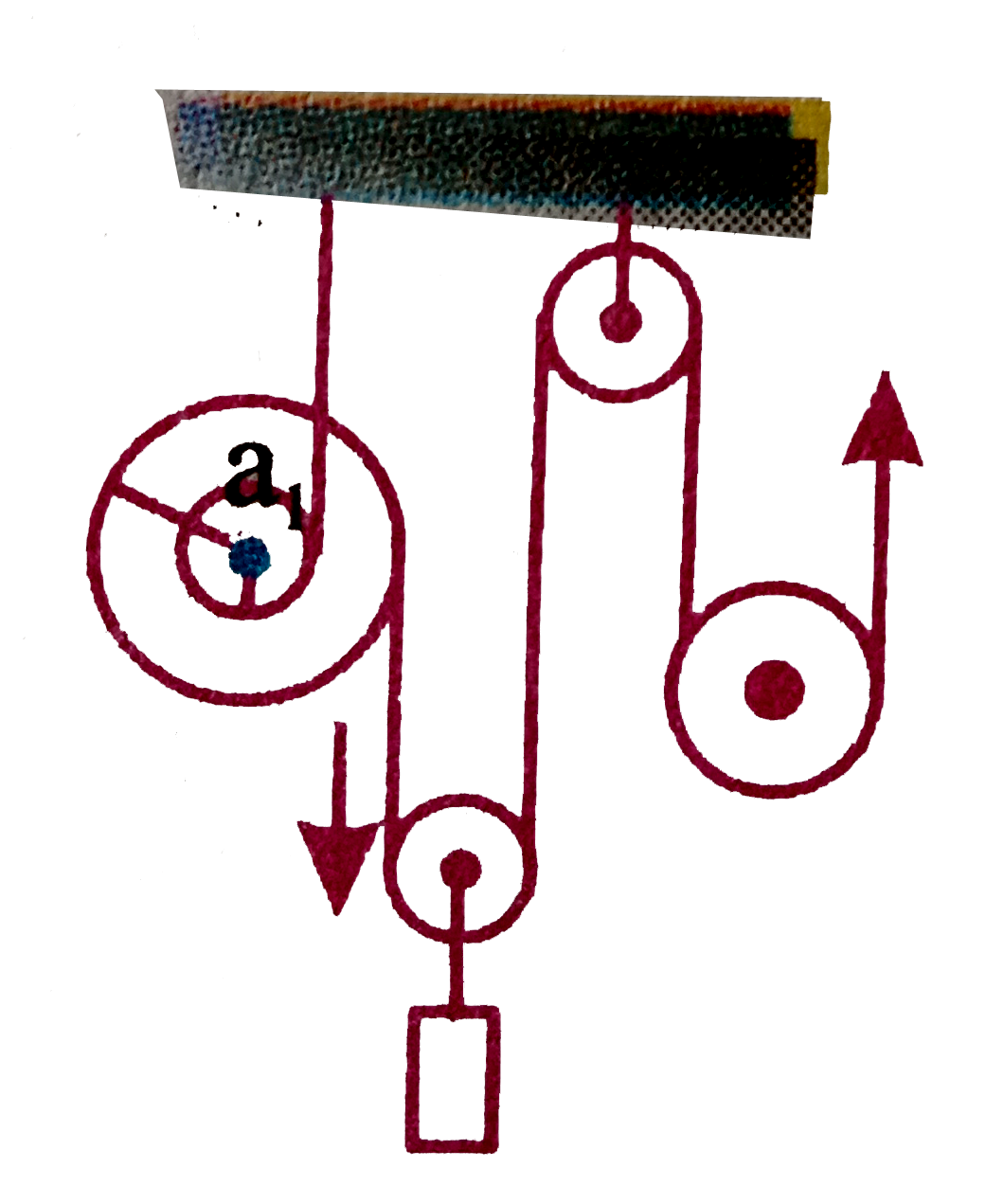
In the figure shown, suppose the compound pulley and the disc have the same angular acceleration, in clockwise direction. If a1 is the upward acceleration of the compound pulley's centre (inner radius r, outer radius 3r), a2 is the downward acceleration of the while a3 is the upward acceleration of the centre of the disc (radius 2r). From kinematic constraints of the thread, the relation between them is:
a2−a32=2a1
a2+a3=a13
a2−a3=3a1
a2+2a3=a1
The correct Answer is:A
(the diagram for this solution is besides to the problem diagram).
At A,a1−rα=0.......(1)
At B,aB=3rα−a1.......(2)
or aB=2a1
aB+aC2=a2
or aC=2a2−2a1.......(3)
From eqns. (3) and (4), we get 2a2−a3=4a1

Topper's Solved these Questions
- SYSTEM OF PARTICLESBook:NARAYNAChapter:SYSTEM OF PARTICLESExercise:Level-V
Explore 72 Videos
- PHYSICAL WORLDBook:NARAYNAChapter:PHYSICAL WORLDExercise:C.U.Q
Explore 10 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION Book:NARAYNAChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTION Exercise:EXERCISE - IV
Explore 39 Videos
Similar Questions

A thread is wound around two discs on either sides. The pulley and the two discs have the same mass and radius. There is no slipping at the pulley and no friction at the hinge. Find out the acceleration of the two discs and the angular acceleration of the pulley.
View SolutionA uniiform disc of radius r spins with angular velocity ω and angular acceleration α. If the centre of mass of the disc has linear acceleration a, find the magnitude and direction of aceeleration of the point 1,2, and 3.

View Solution
Knowledge Check
Starting from the centre of the earth having radius R the variation of g (acceleration due to gravity) is shown by
A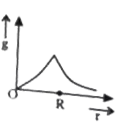 B
B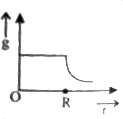 C
C D
D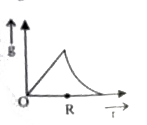
Starting from the centre of the earth having radius R, the variation of g (acceleration due to gravity) is shown by
A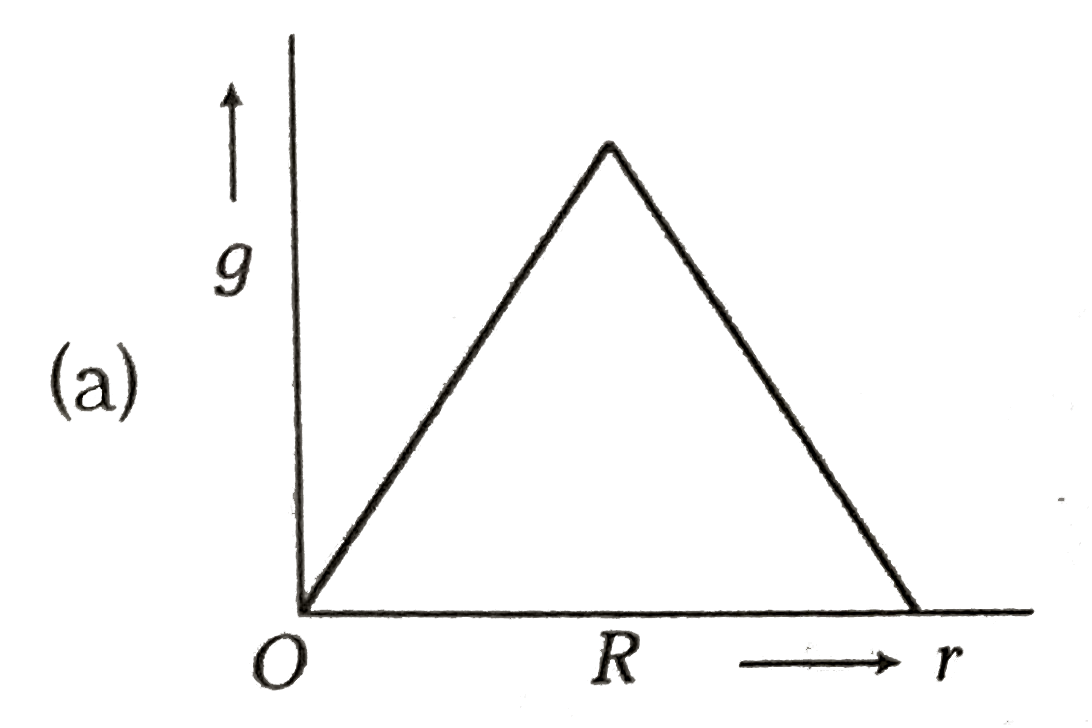 B
B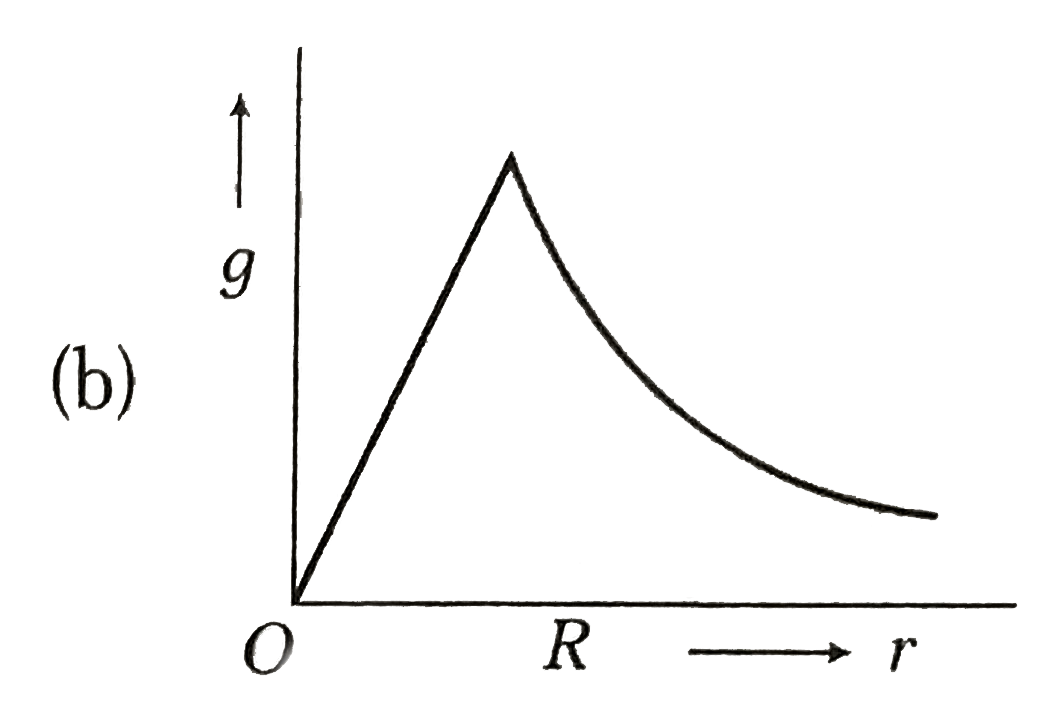 C
C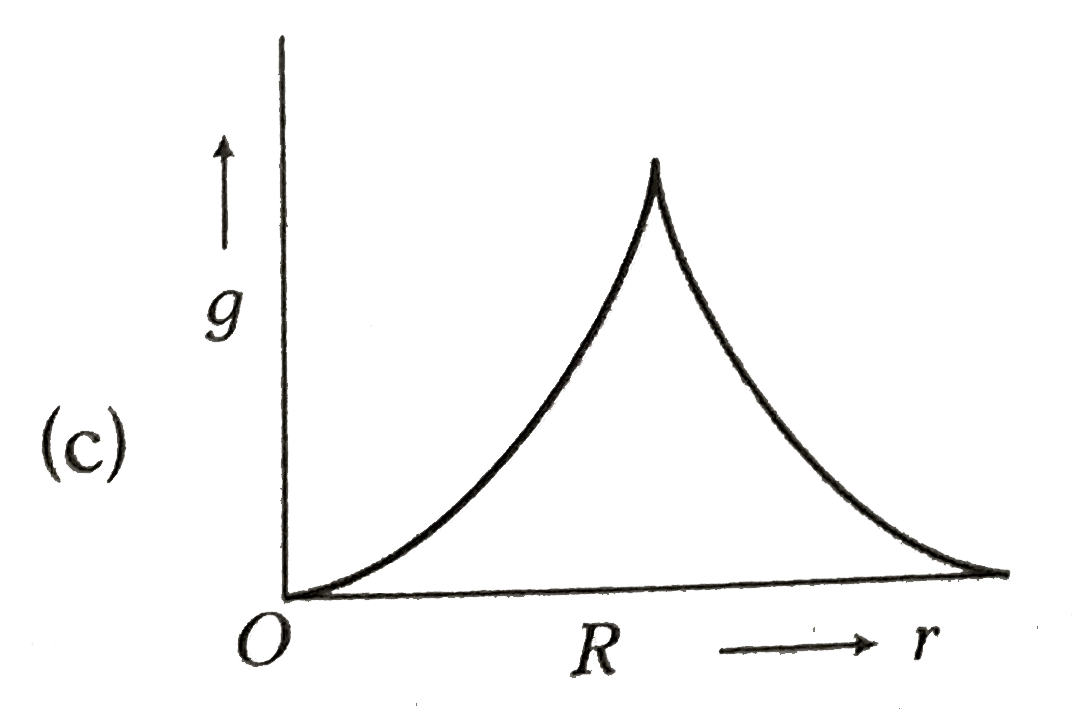 D
D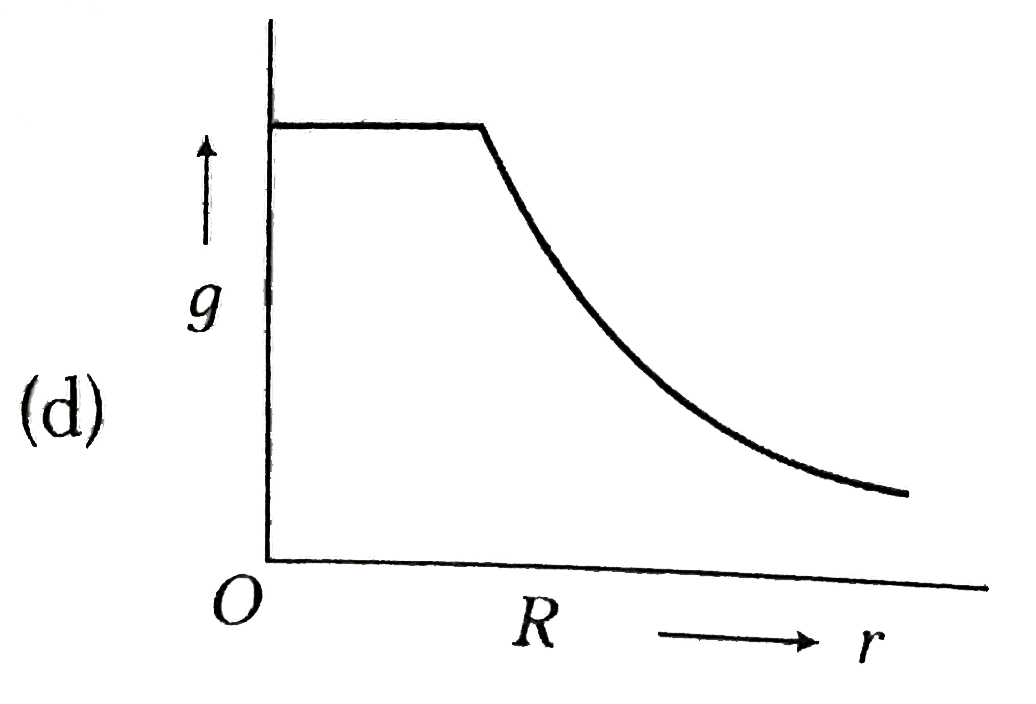
Two identical uniform discs of mass m and radius r are arranged as shown in the figure. If α is the angular acceleration of the lower disc and acm is acceleration of centre of mass of the lower disc, then relation among acm,α and r is
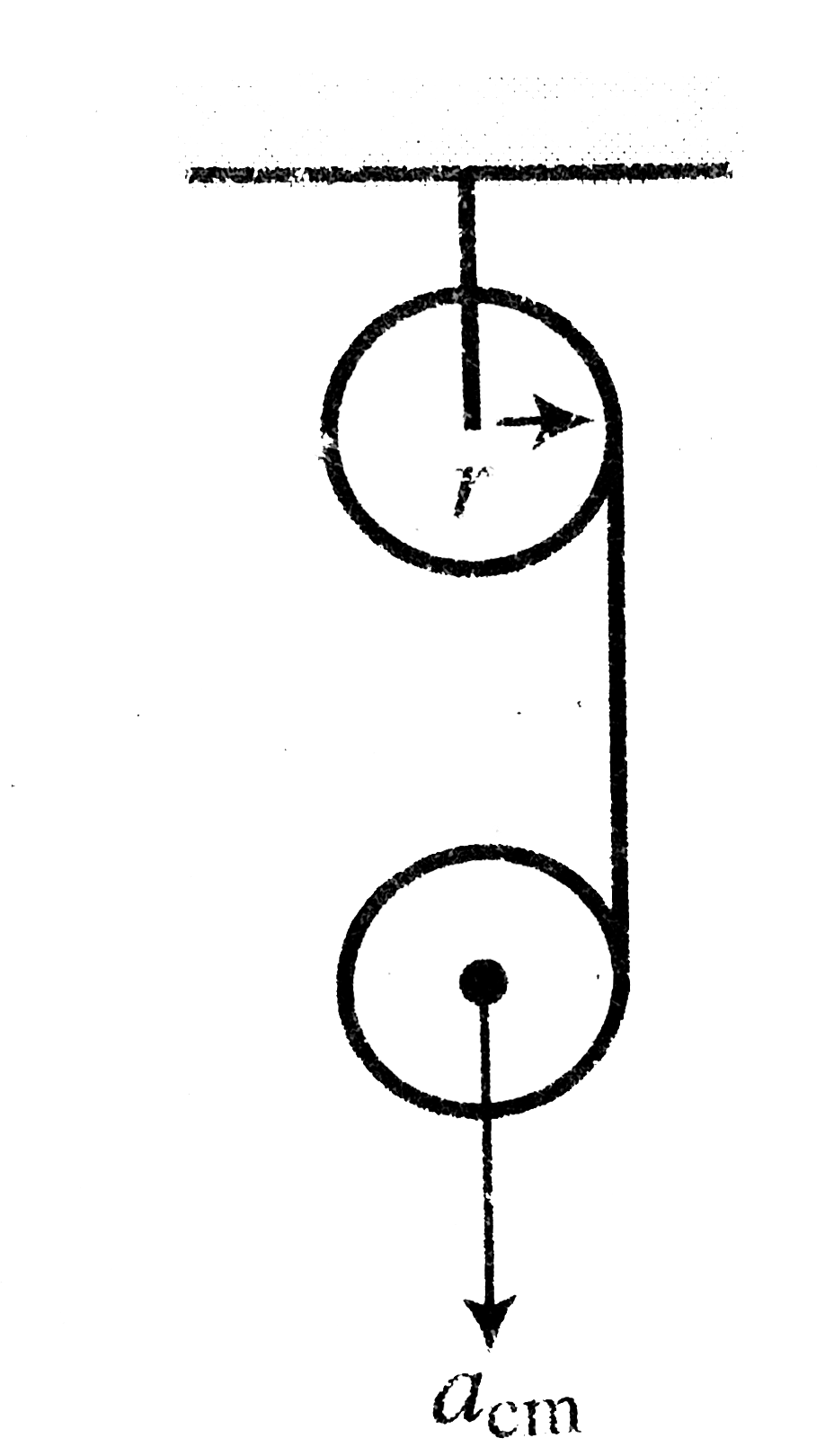 Aacm=αrBacm=2αrCacm=αrDnone of these
Aacm=αrBacm=2αrCacm=αrDnone of these
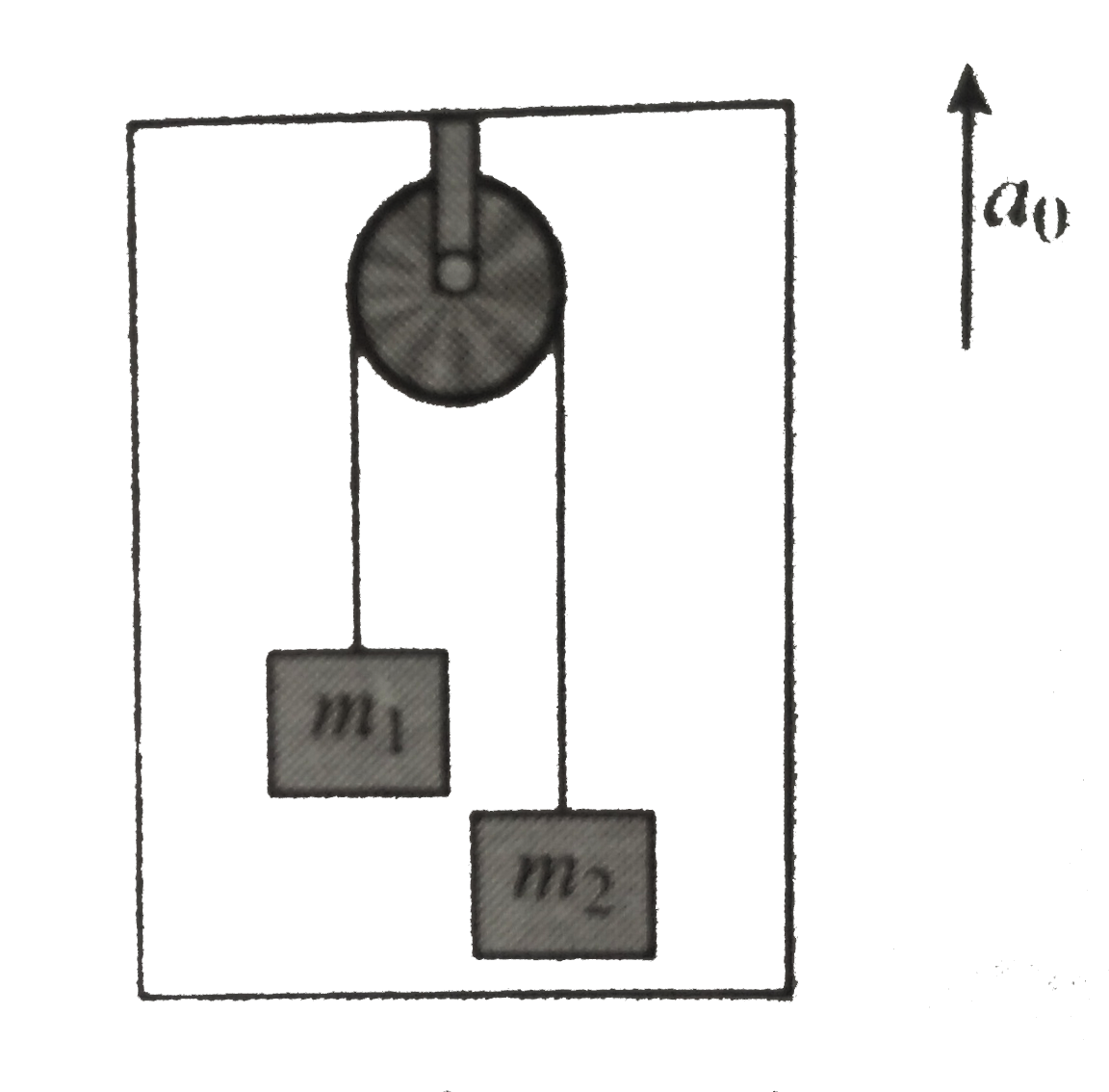
If the pulley is massles and moves with an upward acceleration a0. Find the acceleration of (m1)and(m2) w.r.t to elevator.
View SolutionFrom a uniform circular disc of radius R, a circular disc of radius R/6 and having centre at a distance R/2 from the centre of the disc is removed. Determine the centre of mass of remaining portion of the disc.
View SolutionA hollow cylinder of specific resistance ρ, inner radius R, outer radius 2R and length 1 is as shown in figure. What is the net resistance between the inner and outer surfaces?
View Solution
A ring of radius R rolls on a horizontal surface with constant acceleration a of the centre of mass as shown in figure. If ω is the instantaneous angular velocity of the ring. Then the net acceleration of the point of contact of the ring with gound is
View SolutionA point charge q is placed inside a conducting spherical shell of inner radius 2R and outer radius 3R at a distance of R fro the centre of the shell. The electric potential at the centre of shell will (potential at infinity is zero).
View Solution

