A collar B of mass m is at rest and when it is in the position shown, the spring is unstretched. If another collar A of mass mn strikes it so that B slides a distance 4m on the smooth rod before momentarily stopping, determine the velocity of A just after the impact. The coefficient of restitution is e. The spring constant is k.
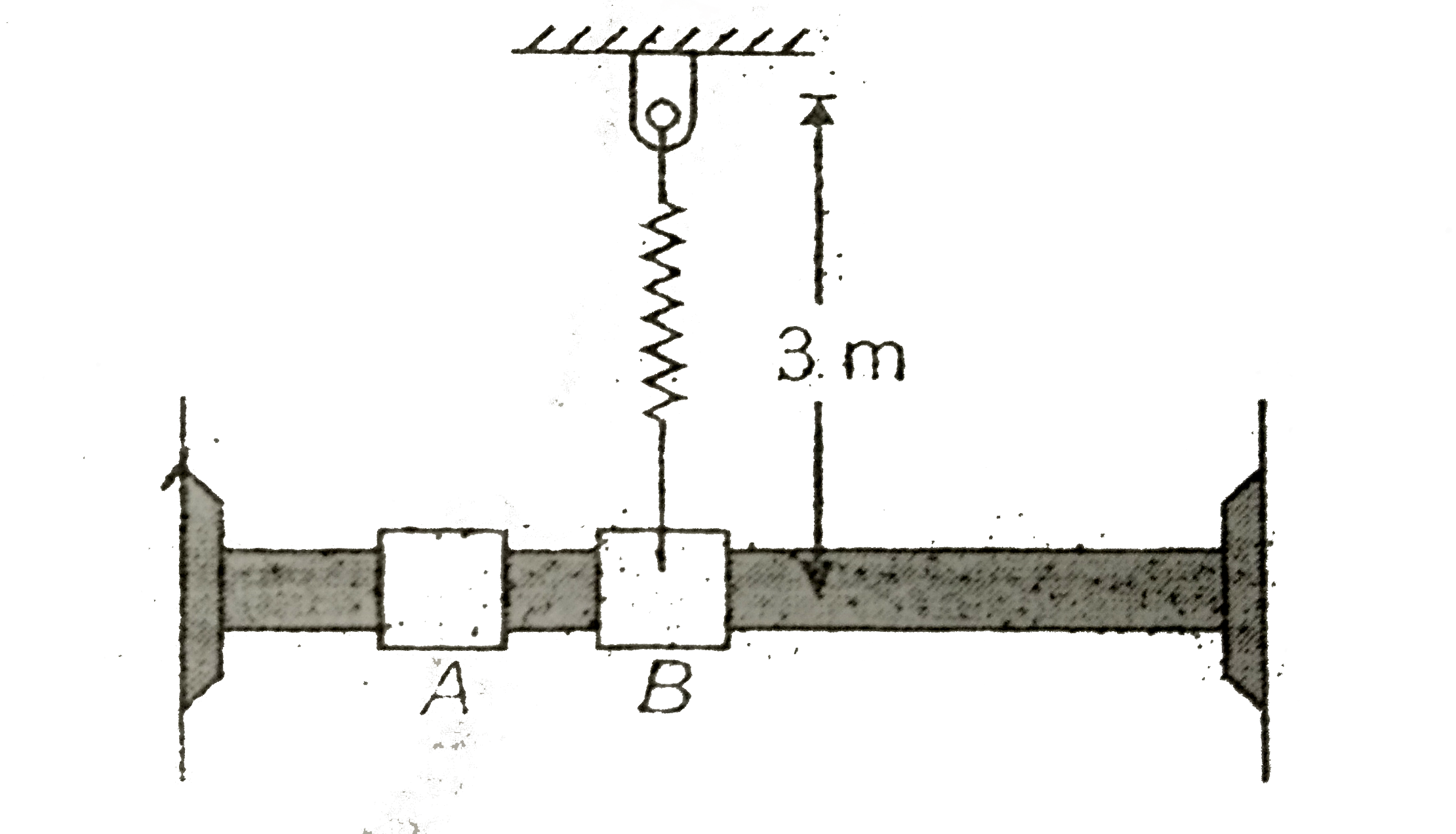
21−ηe1+e√km
Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - AAKASH INSTITUTECHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Assignment (Section - J) Aakash Challengers Questions
13 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - AAKASH INSTITUTECHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Try Yourself
63 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - AAKASH INSTITUTECHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Assignment (Section - H) Multiple True-False Type Questions
4 Videos
- SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITSBOOK - AAKASH INSTITUTECHAPTER - SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITSEXERCISE - Assignment (Section-D (Assertion and reason))
5 Videos
- TEST 1BOOK - AAKASH INSTITUTECHAPTER - TEST 1EXERCISE - EXERCISE
9 Videos
Similar Questions
A smooth wedge of mass M is kept at rest on a smooth horizontal surface . Inclined face of the wedge make an angle θ with the horizontal . A particle of mass m collides normal to inclined face of wedge . If speed of the particle just before collision is u and coefficient of restitution is e then find velocity of wedge after collision .
View SolutionA ball of mass 2m impinges directly on a ball of mass m, which is at rest. If the velocity with which the larger ball impinges be equal to the velocity of the smaller mass after impact then the coefficient of restitution :-
View Solution
Knowledge Check
A ball of mass 2m impinges directly on a ball of mass m, which is at rest. If the velocity with which the larger ball impringes be equal to the velocity of the smaller mass after impact then the coefficient of restitution :-
A13B34C12D25A particle of mass m, collides with another stationary particle of mass M. If the particle m stops just after collision, then the coefficient of restitution for collision is equal to
A1BmMCM−mM+mDmM+mA sphere of mass m falls on a smooth hemisphere of mass M resting with its plane face on smooth horizontal table, so that at the moment of impact, line joining the centres makes an angle with the vertical. The velocity of sphere just before impact is u and e is the coefficient of restitution.
AThe velocity of hemisphere after impact will be zeroBThe hemisphere will move with a velocity v=musinαMcos2αCThe hemisphere will move with a velocity v=mucosα(1+e)(M+m)DNone of these
A ball of mass m moving with velocity u strikes another identical ball at rest. Find the velocities of the balls after the collision if the coefficient of restitution is e and the collision is head -on. Also , calculate the loss in K.E.
View SolutionA uniform rod of mass m and length l is lying on a smooth table. An impulse J acts on the rod momentarily as shown in figure at point R. Just after that:


View SolutionA ball of mass M strikes another smooth ball of mass m at rest. If they separate in mutually perpendicular directions, then the coefficient of impact (e) is :
View SolutionA mass m=8kg is attached to a spring as shown in figure and held in position so that the spring remains unstretched. The spring constant is 200N/m. The mass m is then released and begins to undergo small oscillations. The maximum velocity of the mass will be (g=10m/s2)
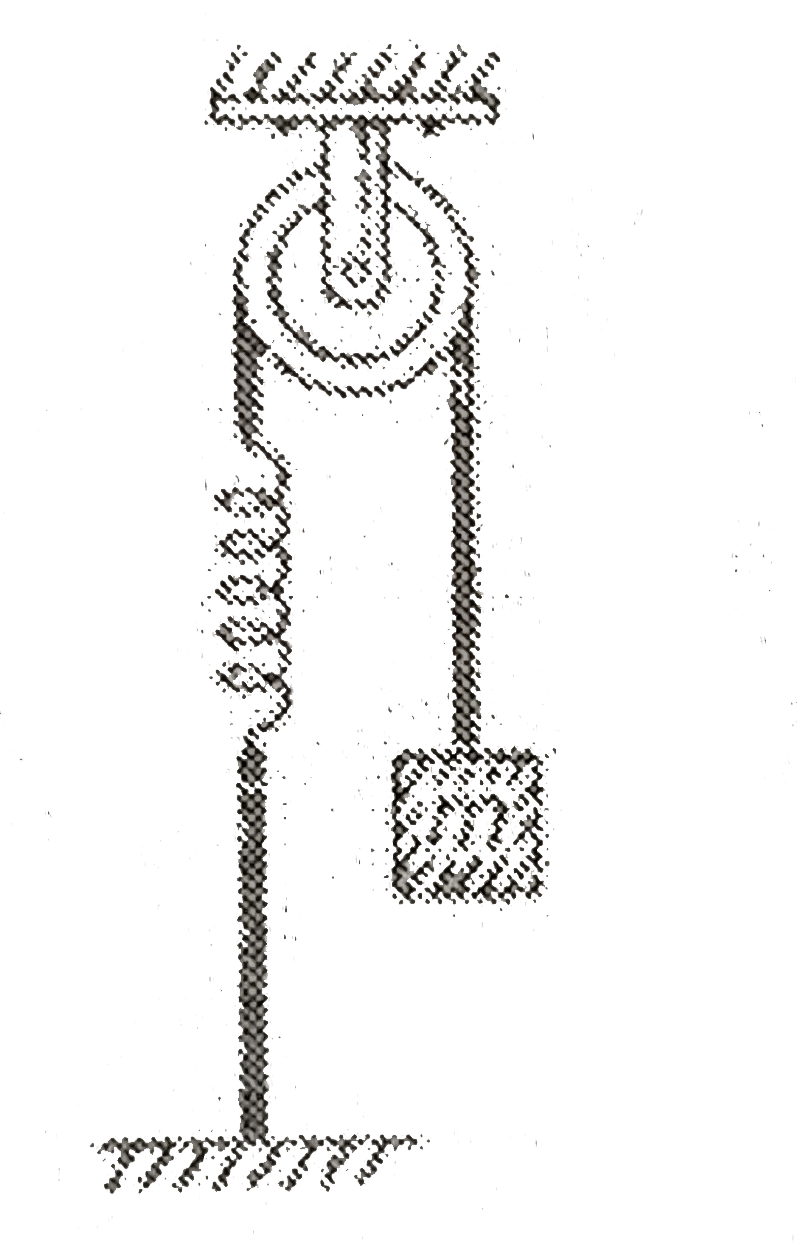
View SolutionA moving block having mass m , collides with another stationary block having mass 4m. The lighter block comes to rest after collision. When the initial velocity of the block is v, then the value of coefficient of restitution (e) will be
View Solution
