Find the acceleration of centre of mass of the blocks of masses m1,m2(m1>m2) in Atwood's machine.
To find the acceleration of the center of mass (ACM) of the blocks of masses m1 and m2 in an Atwood machine, we can follow these steps:
Step 1: Understand the system
In an Atwood machine, there are two masses, m1 and m2, connected by a string over a pulley. Given that m1>m2, the heavier mass m1 will accelerate downwards while m2 will accelerate upwards.
Step 2: Write down the forces acting on the masses
The forces acting on the masses are:
- For mass m1: The downward force is m1g (weight) and the upward force is the tension T.
- For mass m2: The upward force is m2g (weight) and the downward force is the tension T.
Step 3: Apply Newton's second law
For mass m1:
m1g−T=m1a
For mass m2:
T−m2g=m2a
Step 4: Solve for tension T
From the first equation:
T=m1g−m1a
From the second equation:
T=m2g+m2a
Setting the two expressions for T equal to each other:
m1g−m1a=m2g+m2a
Step 5: Rearrange and solve for acceleration a
Rearranging the equation gives:
m1g−m2g=m1a+m2a
(m1−m2)g=(m1+m2)a
Now, solving for a:
a=(m1−m2)gm1+m2
Step 6: Find the acceleration of the center of mass
The acceleration of the center of mass ACM can be found using the formula:
ACM=m1a1+m2a2m1+m2
Here, a1=−a (downward for m1) and a2=a (upward for m2):
ACM=m1(−a)+m2(a)m1+m2
Substituting a:
ACM=−m1((m1−m2)gm1+m2)+m2((m1−m2)gm1+m2)m1+m2
Factoring out (m1−m2)gm1+m2:
ACM=(m2−m1)g(m1+m2)2
Since m1>m2, ACM will be negative, indicating that the center of mass moves downward.
Final Result
Thus, the acceleration of the center of mass is:
ACM=(m1−m2)g(m1+m2)2
In an Atwood machine, there are two masses, m1 and m2, connected by a string over a pulley. Given that m1>m2, the heavier mass m1 will accelerate downwards while m2 will accelerate upwards.
The forces acting on the masses are:
- For mass m1: The downward force is m1g (weight) and the upward force is the tension T.
- For mass m2: The upward force is m2g (weight) and the downward force is the tension T.
For mass m1:
m1g−T=m1a
For mass m2:
T−m2g=m2a
From the first equation:
T=m1g−m1a
From the second equation:
T=m2g+m2a
Setting the two expressions for T equal to each other:
m1g−m1a=m2g+m2a
Rearranging the equation gives:
m1g−m2g=m1a+m2a
(m1−m2)g=(m1+m2)a
Now, solving for a:
a=(m1−m2)gm1+m2
The acceleration of the center of mass ACM can be found using the formula:
ACM=m1a1+m2a2m1+m2
Here, a1=−a (downward for m1) and a2=a (upward for m2):
ACM=m1(−a)+m2(a)m1+m2
Substituting a:
ACM=−m1((m1−m2)gm1+m2)+m2((m1−m2)gm1+m2)m1+m2
Factoring out (m1−m2)gm1+m2:
ACM=(m2−m1)g(m1+m2)2
Since m1>m2, ACM will be negative, indicating that the center of mass moves downward.
Thus, the acceleration of the center of mass is:
ACM=(m1−m2)g(m1+m2)2
Topper's Solved these Questions
- SYSTEM OF PARTICLESBook:NARAYNAChapter:SYSTEM OF PARTICLESExercise:C.U.Q.
Explore 83 Videos
- SYSTEM OF PARTICLESBook:NARAYNAChapter:SYSTEM OF PARTICLESExercise:Level-1(C.W.)
Explore 64 Videos
- PHYSICAL WORLDBook:NARAYNAChapter:PHYSICAL WORLDExercise:C.U.Q
Explore 10 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION Book:NARAYNAChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTION Exercise:EXERCISE - IV
Explore 39 Videos
Similar Questions
Two bodies of masses m1andm2(<m1) are connected to the ends of a massless cord and allowed to move as shown in figure. The pulley is both massless and frictionless. The acceleration of the centre of mass is (m1−m2)n(m1+m2)2g. Find the value of n.

View SolutionThree blocks, placed on smooth horizontal surface are connected by ideal string and a disc shaped pulley of radius r, and mass m. Find the accelerations of the blocks. Masses of the blocks are given as M1=10kg,M2=5kg,M3=2kg,m=2kg.
View Solution
Knowledge Check
Where will be the centre of mass on combining two masses m and M(M>m)?
ATowards mBTowards MCBetween m and MDAnywhereWhere will be the centre of mass on combining two masses m and M(M>m)?
ATowards mBTowards MCBetween m and MDAnywhere
Assuming all the surfaces to be smooth, find the acceleration of the triangular block of mass M when the block of mass m slides on it.

View SolutionFind the acceleration of each block in the figure shown below, in terms of their masses m1,m2 and g. Neglect any friction.

View Solution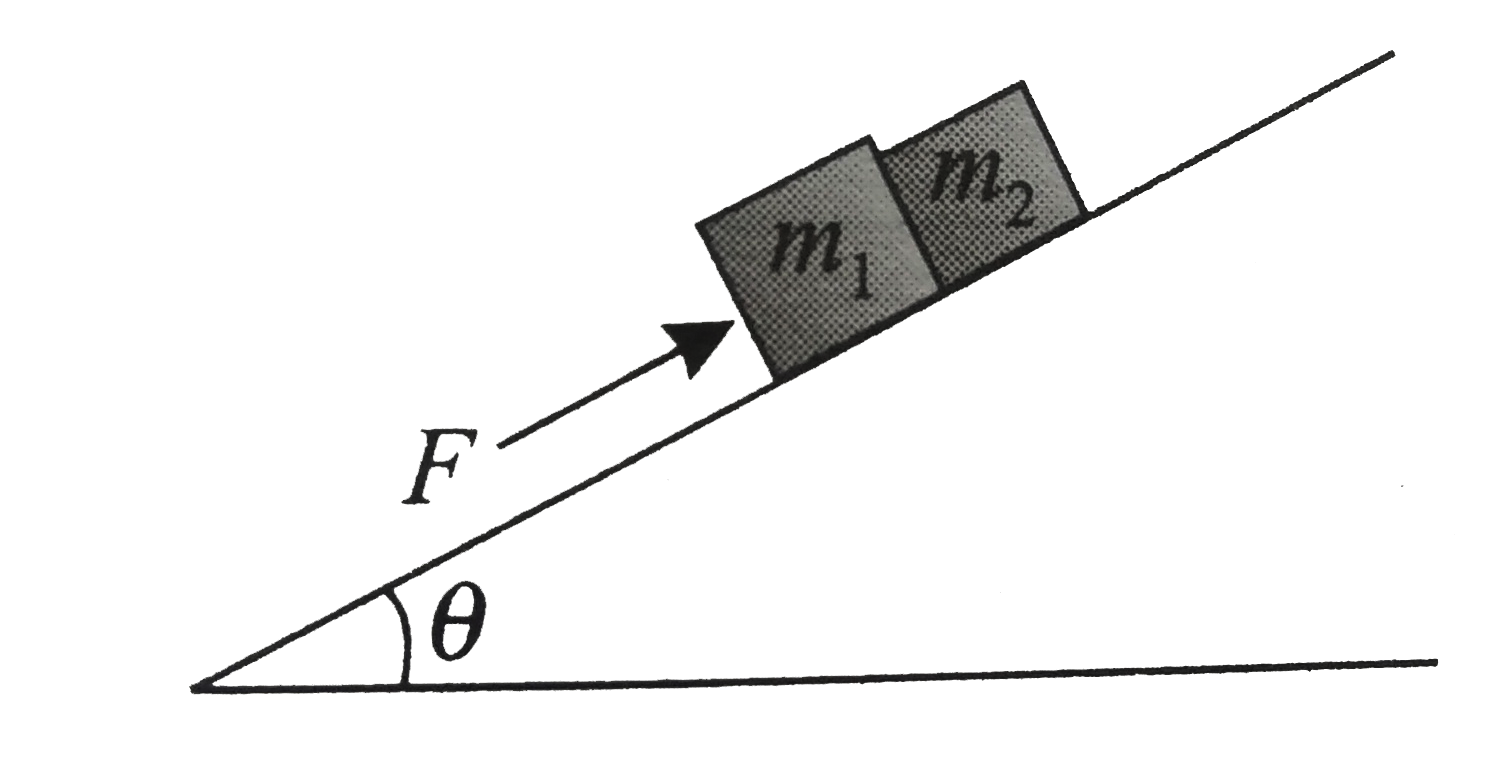
Two blocks are placed at rest on a smooth fixed inclined place. A force F acts on block of mass m1 and is parallel to the inclined plane as shown in figure. Both blocks move up the incline. Then
(i) Draw free body diagram blocks of mass m1 and blocks mass m2
(ii) Find acceleration of blocks of mass m1 and blocks mass m2
(iii) Find normal reaction between the blocks of mass m1 and m2
View SolutionPlot a graph showing variation of de-broglie wavelength λ versus 1/√V, where V is accelerating potential for two particle A and P carrying same charge but of masses m1andm2(m1>m2). Which one of the two represents a particle of smaller mass and why?
View SolutionA light string passing over a smooth light pulley connects two blocks of masses m_(1) and m_(2) (vertically).If the acceleration of the system is g/8 then the ratio of masses "m_(1)" to "m_(2)" is "(" take "m_(1)>m_(2)]
View SolutionIn an atwood machine the two blocks have massess 1kg and 3kg. The pulley is massless and frictionless and string is light. The acceleration of the centre of mass (in m/s2) of this system is 0.5x. Find the value of x.
View Solution

