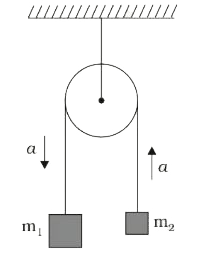
Two bodies of masses m1andm2(<m1) are connected to the ends of a massless cord and allowed to move as shown in figure. The pulley is both massless and frictionless. The acceleration of the centre of mass is (m1−m2)n(m1+m2)2g. Find the value of n.
The correct Answer is:2
If →a is the acceleration ofm1 then −→a is the acceleration of m2.
We know that (m1+m2)→Acm.m1→a1+m2→a2
or (m1+m2)→Acm=m1→a−m2→a or →acm.=m1−m2m1+m2→a
But, →a=m−1−m2m1+m2→g [connected - body problem] ∴ →Acm.=(m1−m2)2(m1+m2)2→g.
Similar Questions
Two bodies of mass m1andm2 are initially at rest placed infinite distance apart. They are then allowed to move towards each other under mutual gravitational attaction. Show that their relative velocity of approach at separation r betweeen them is
v=√2G(m1+m2)r
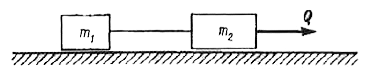
View SolutionTwo bodies with masses m1 and m2>m1 connected by a thread lie on a smooth table. A force Q is first applied to the larger and then to the smaller of the bodies (Fig.). Is the tension of the thread in both cases the same?
View Solution
Knowledge Check
Two bodies with masses m1 and m2(m1>m2) are joined by a string passing over fixed pulley. Assume masses of the pulley and thread negligible. Then the acceleration of the centre of mass of the system (m1+m2) is
A(a) (m1−m2m1+m2)gB(b) (m1−m2m1+m2)2gC(c) m1gm1+m2D(d) m2gm1+m2Two bodies with masses m1 and m2(m2>m)connected by a thread lie on a smooth table. A force Q is first applied to the larger mass and then to the smaller mass. The ratio of tensions in the thread in the two cases will be
 Am1m2Bm1m2Cm2m1+m2Dm1m2−m2
Am1m2Bm1m2Cm2m1+m2Dm1m2−m2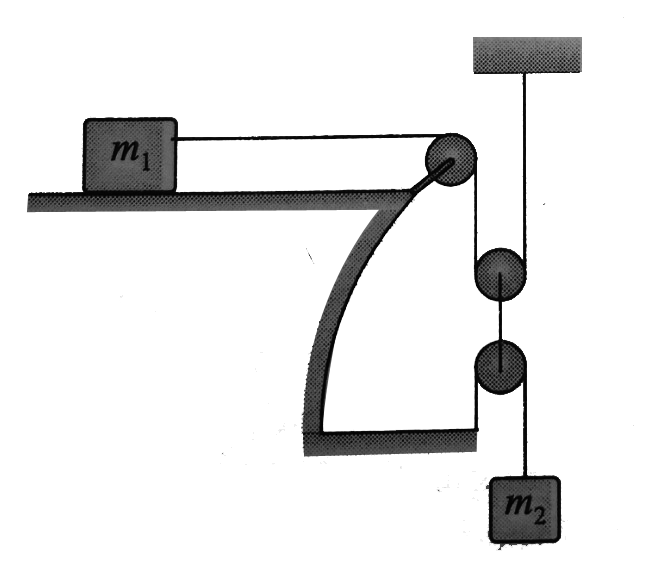
Two blocks of masses m1 and m2 are connected as shown in the figure. The acceleration of the block m2 is :Am2gm1+m2Bm1gm1+m2C4m2g−m1gm1+m2Dm2gm1+4m2
Two bodies of masses 'm' and 2m are separated by a distance d'. The body of mass 'm' attracts another body of mass 2m with a force F, then the body of mass 2m attracts m with the force of______________
View SolutionTwo bodies of masses 2 m and m have their K.E. in the ratio 8 : 1, then their ratio of momenta is
View SolutionTwo bodies of masses 2 m and m have their K.E. in the ratio 8 : 1, then their ratio of momenta is
View SolutionTwo bodies of masses 1kgand2kg are moving in two perpendicular direction with velocities 1m/sand2m/s as shown in figure. The velocity of the centre of mass (in magnitide) of the system will be :
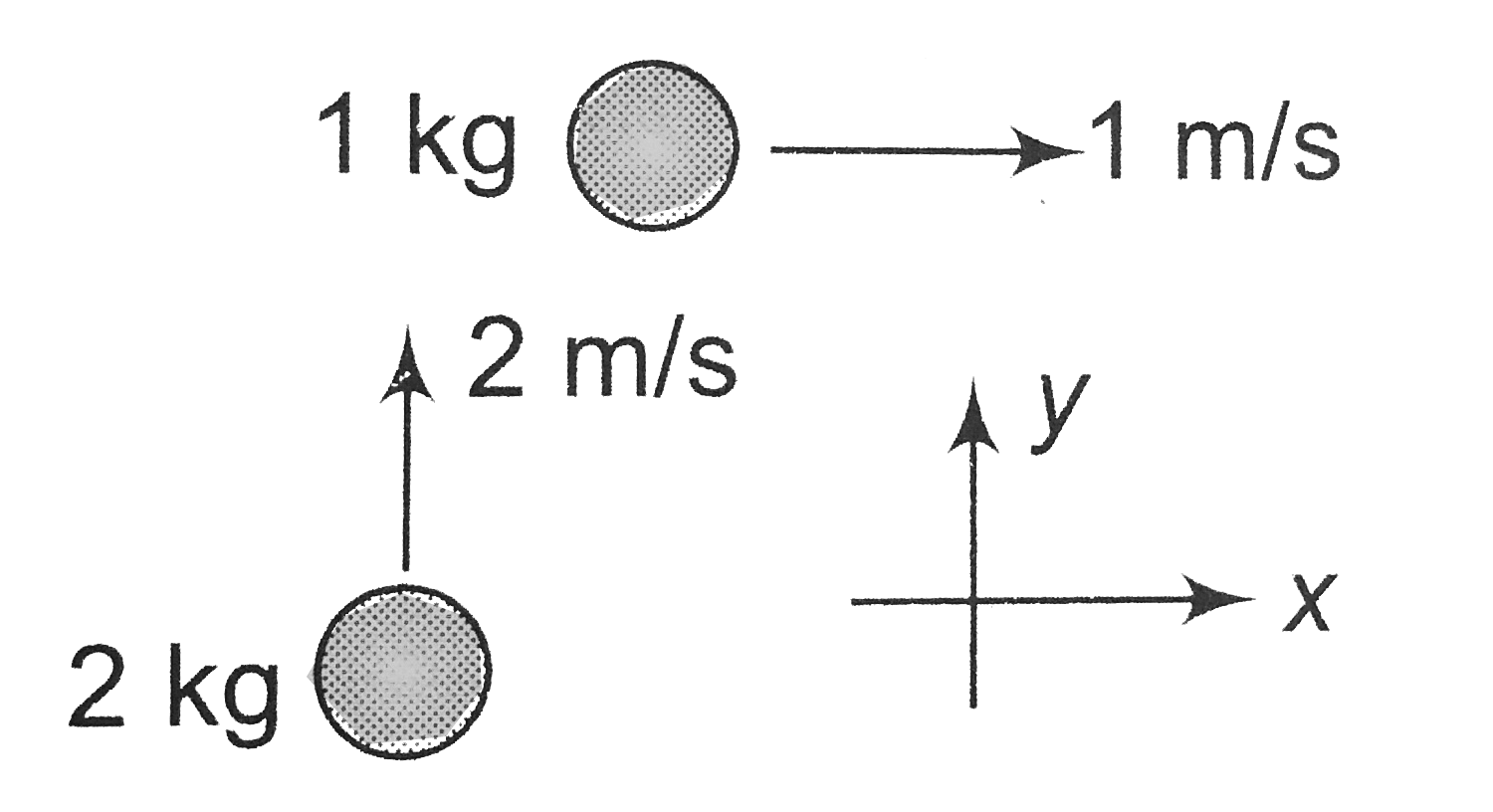
View SolutionTwo bodies of masses 3 m and m have their K.Einh 27:1 then the ratio of the momentum is
View Solution

