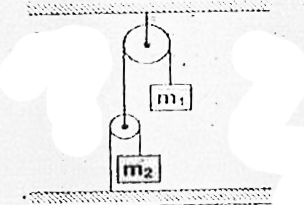
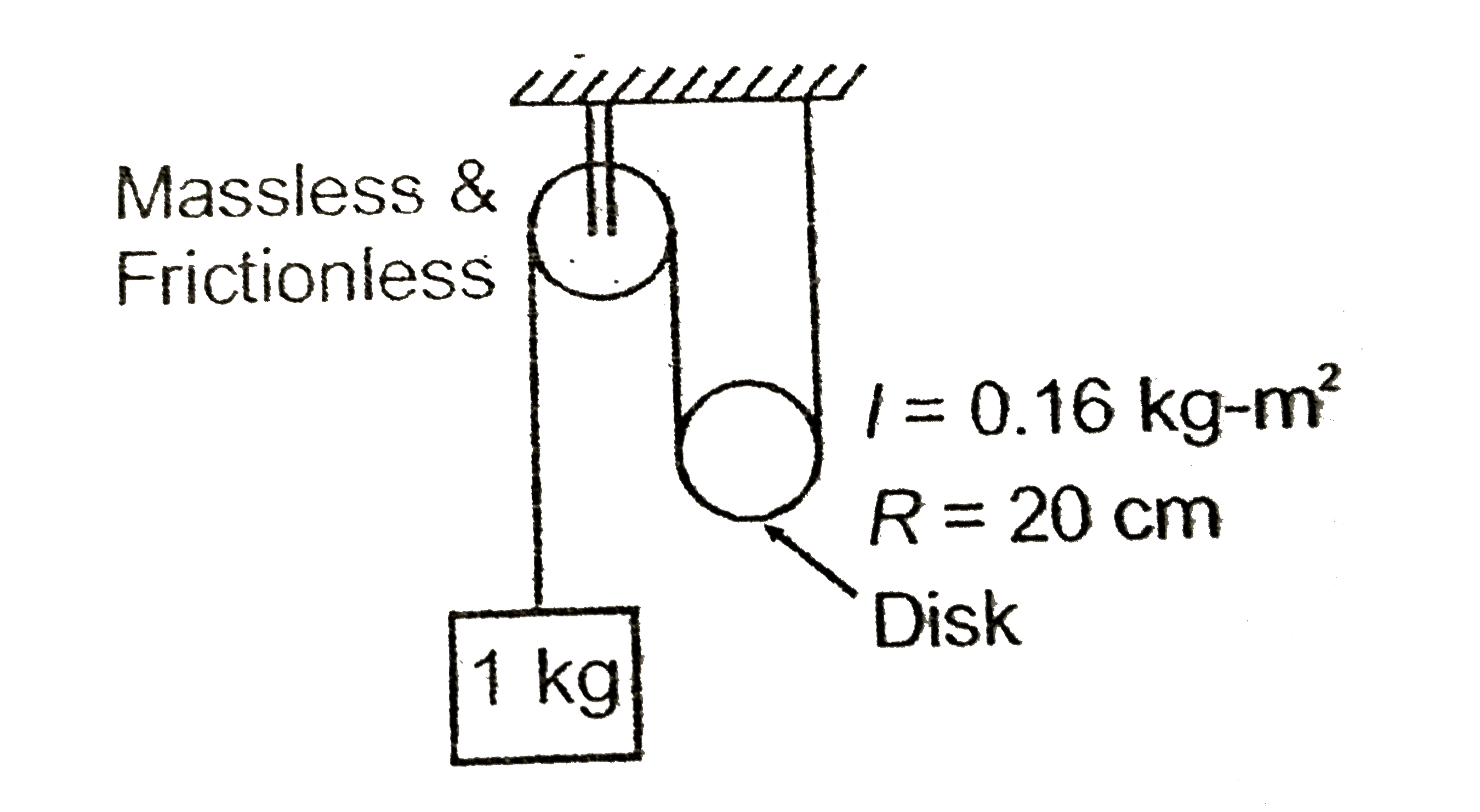In an atwood machine the two blocks have massess 1kg and 3kg. The pulley is massless and frictionless and string is light. The acceleration of the centre of mass (in m/s2) of this system is 0.5x. Find the value of x.
To solve the problem of the Atwood machine with masses of 1 kg and 3 kg, we will follow these steps:
Step 1: Identify the forces acting on each mass
- For the 3 kg mass (m1):
- Weight (W1) = m1 * g = 3 kg * 10 m/s² = 30 N (downward)
- For the 1 kg mass (m2):
- Weight (W2) = m2 * g = 1 kg * 10 m/s² = 10 N (downward)
Step 2: Write the equations of motion for each mass
- For the 3 kg mass (m1):
m1⋅g−T=m1⋅a(1)
where T is the tension in the string and a is the acceleration of the system.
- For the 1 kg mass (m2):
T−m2⋅g=m2⋅a(2)
Step 3: Substitute the values into the equations
From equation (1):
30−T=3a(3)
From equation (2):
T−10=1a(4)
Step 4: Solve the equations simultaneously
Add equations (3) and (4):
(30−T)+(T−10)=3a+1a
This simplifies to:
30−10=4a
20=4a
a=204=5m/s2
Step 5: Calculate the acceleration of the center of mass (ACM)
The total mass of the system (M) is:
M=m1+m2=3kg+1kg=4kg
The acceleration of the center of mass (ACM) can be calculated using the formula:
ACM=ΣmiaiΣmi
Where ai is the acceleration of each mass. Since the 1 kg mass is moving upward with acceleration 5m/s2 and the 3 kg mass is moving downward with the same acceleration:
ACM=(1⋅5)+(3⋅−5)4=5−154=−104=−2.5m/s2
The negative sign indicates that the center of mass is accelerating downward.
Step 6: Relate the acceleration of the center of mass to the given expression
According to the problem, the acceleration of the center of mass is given as 0.5x:
0.5x=2.5
Step 7: Solve for x
To find the value of x:
x=2.50.5=5
Final Answer
The value of x is 5.
- For the 3 kg mass (m1):
- Weight (W1) = m1 * g = 3 kg * 10 m/s² = 30 N (downward)
- For the 1 kg mass (m2):
- Weight (W2) = m2 * g = 1 kg * 10 m/s² = 10 N (downward)
- For the 3 kg mass (m1):
m1⋅g−T=m1⋅a(1)
where T is the tension in the string and a is the acceleration of the system.
T−m2⋅g=m2⋅a(2)
From equation (1):
30−T=3a(3)
T−10=1a(4)
Add equations (3) and (4):
(30−T)+(T−10)=3a+1a
This simplifies to:
30−10=4a
20=4a
a=204=5m/s2
The total mass of the system (M) is:
M=m1+m2=3kg+1kg=4kg
ACM=ΣmiaiΣmi
Where ai is the acceleration of each mass. Since the 1 kg mass is moving upward with acceleration 5m/s2 and the 3 kg mass is moving downward with the same acceleration:
ACM=(1⋅5)+(3⋅−5)4=5−154=−104=−2.5m/s2
The negative sign indicates that the center of mass is accelerating downward.
According to the problem, the acceleration of the center of mass is given as 0.5x:
0.5x=2.5
To find the value of x:
x=2.50.5=5
The value of x is 5.
Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBook:AAKASH INSTITUTEChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTIONExercise:Assignment (Section - H) Multiple True-False Type Questions
Explore 4 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBook:AAKASH INSTITUTEChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTIONExercise:Assignment (Section - I) Subjective Type Questions
Explore 8 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBook:AAKASH INSTITUTEChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTIONExercise:Assignment (Section - F) Matrix-Match Type Questions
Explore 8 Videos
- SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITSBook:AAKASH INSTITUTEChapter:SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITSExercise:Assignment (Section-D (Assertion and reason))
Explore 5 Videos
- TEST 1Book:AAKASH INSTITUTEChapter:TEST 1Exercise:EXERCISE
Explore 9 Videos
Similar Questions
Knowledge Check
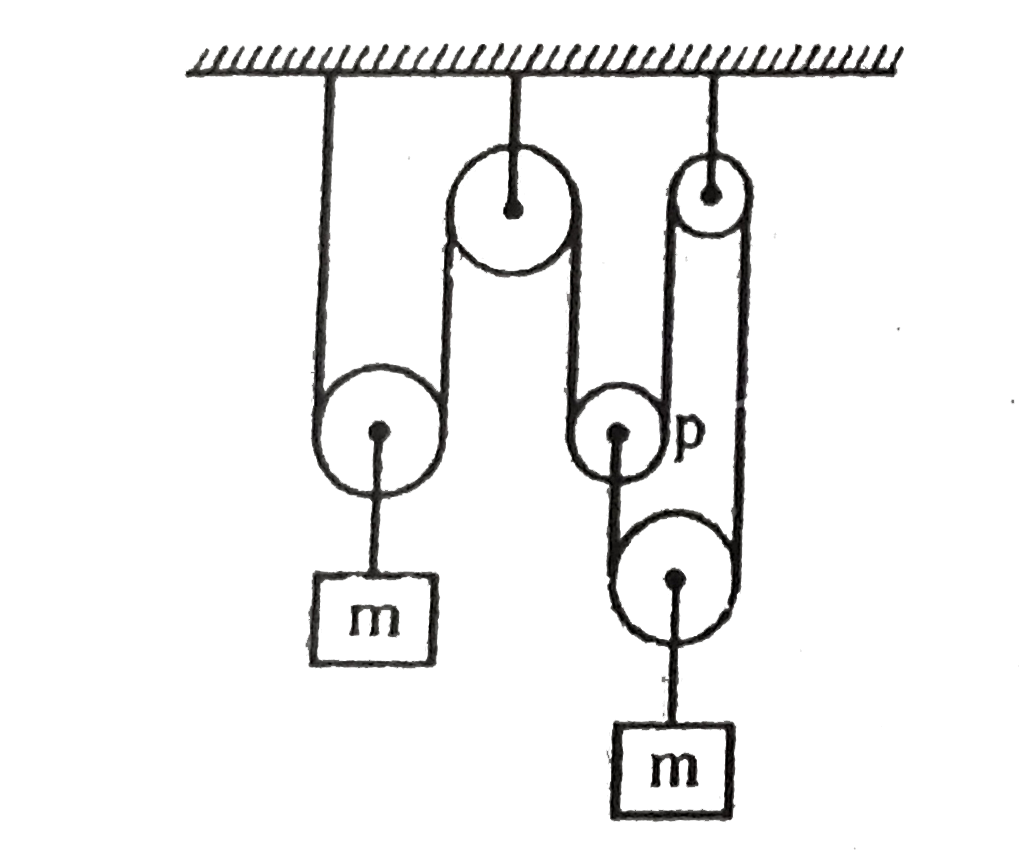
Find the acceleration of the block of mass m. Assume pulleys are massless and frictionless.
 Ag/3B2g3Cg2DNone
Ag/3B2g3Cg2DNoneTwo bodies of massless string passing over a frictionless pulley. The acceleration of the system is (g=9.8m/s2)
A4.9m/s2B2.45m/s2C1.4m/s2D9.5m/s2Two blocks of masses 3 kg and 6 kg are connected by a string as shown in the figure over a frictionless pulley. The acceleration of the system is
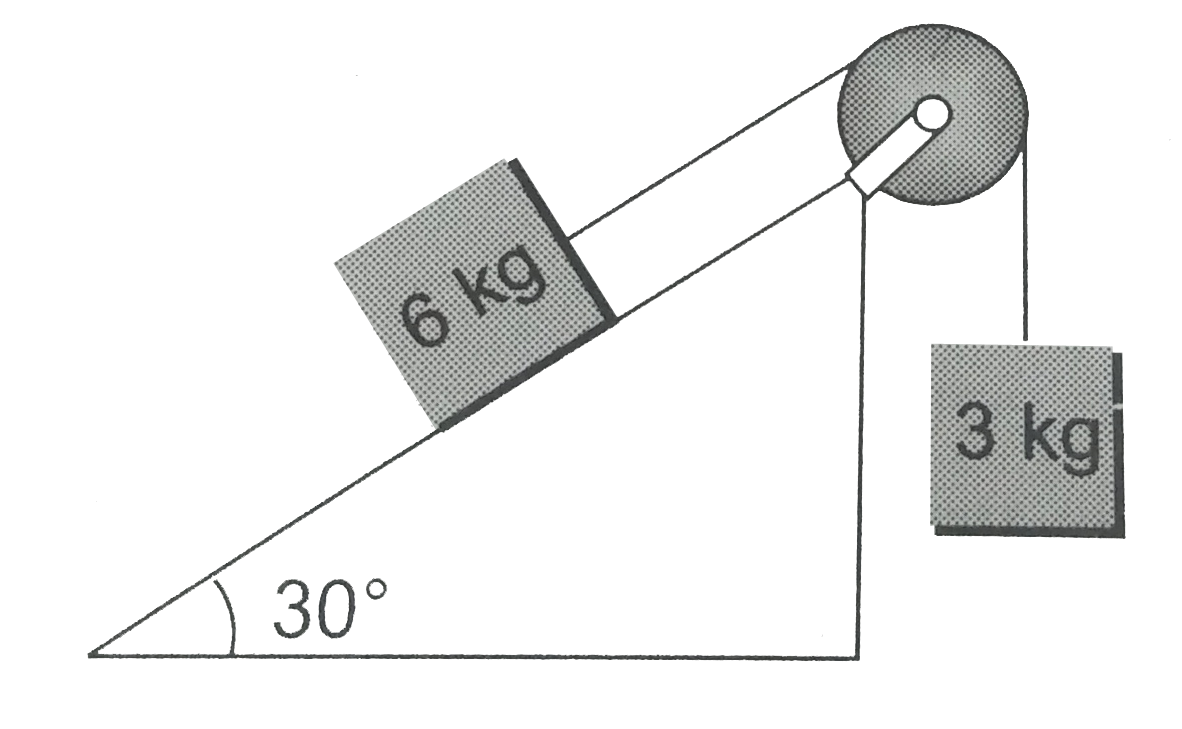 A4m/s2B2m/s2CzeroD6m/s2
A4m/s2B2m/s2CzeroD6m/s2
Find the relation between acceleration of the two blocks m1andm2. Assume pulleys are massless and frictionless and the strings are inextensible .
View SolutionTwo bodies of mass 3kg and 4kg are suspended at the ends of massless string passing over a frictionless pulley. The acceleration of the system is (g=9.8m/s2)
View SolutionTwo bodies of mass 3 kg and 4 kg are suspended at the ends of massless string passing over a frictionless pulley. The acceleration of the system is (g=9.8m/s2)
View SolutionTwo masses m and m (m>m) are connected by massless flexible and inextensible string passed over massless and frictionless pulley. The acceleration of centre of mass is
View SolutionIn the system shown in figure mB=4kg , and mA=2kg . The pulleys are massless and friction is absent everywhere. The acceleration of block A is.

View Solution