Two identical blocks each of mass ''M'' are tied to the ends of a string and the string is laid over a smooth fixed pulley. Initially the masses are held at rest at the same level. What fraction of mass must be removed from one block and added to the other, so that is has an acceleration of 1/5th of the acceleration due to gravity ? .
1/10
1/5
2/5
1/20
The correct Answer is:B
F=ma,a=(m1−m2m1+m2)g
Topper's Solved these Questions
- NEWTONS LAWS OF MOTIONBook:NARAYNAChapter:NEWTONS LAWS OF MOTIONExercise:LEVEL -III
Explore 31 Videos
- NEWTONS LAWS OF MOTIONBook:NARAYNAChapter:NEWTONS LAWS OF MOTIONExercise:NCERT BASED QUESTION
Explore 33 Videos
- NEWTONS LAWS OF MOTIONBook:NARAYNAChapter:NEWTONS LAWS OF MOTIONExercise:LEVEL -I (C.W)
Explore 47 Videos
- MOTION IN A STRAIGHT LINEBook:NARAYNAChapter:MOTION IN A STRAIGHT LINEExercise:Level 2 H.W
Explore 29 Videos
- OSCILLATIONSBook:NARAYNAChapter:OSCILLATIONSExercise:EXERCISE - IV
Explore 41 Videos
Similar Questions
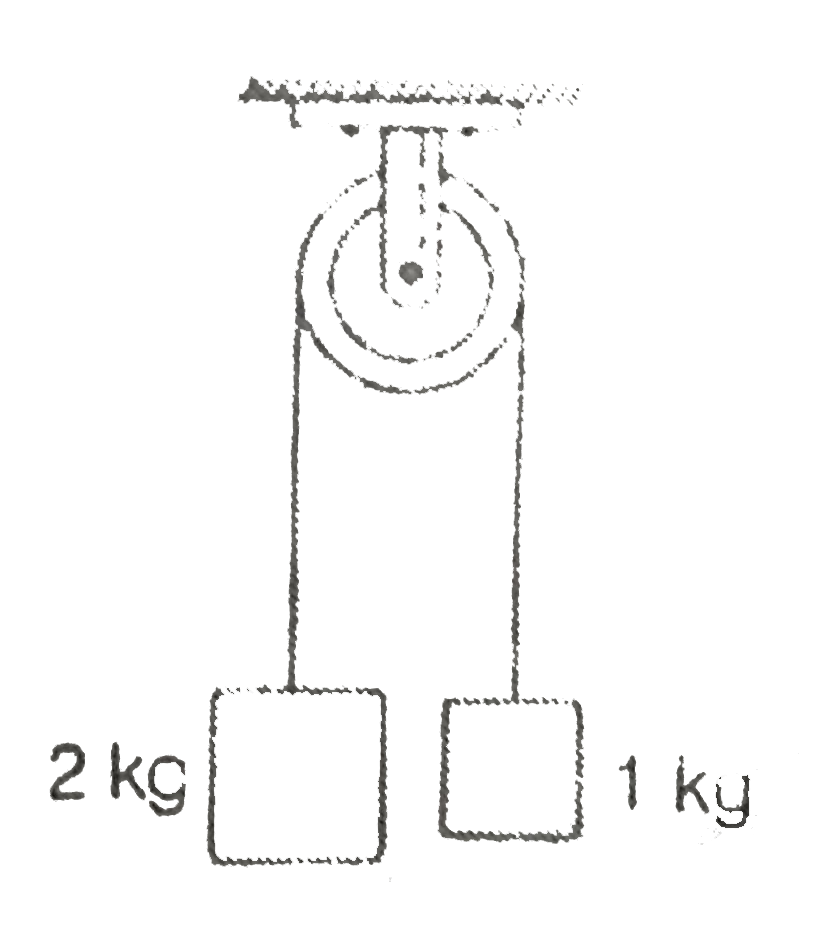
Two blocks of masses 2 kg and 1 kg respectively are tied to the ends of a string which passes over a light frictionless pulley . The masses are held at rest at the same horizontal level and then released . The distance traversed by centre of mass in 2 s is ( g = 10 m/s2)
View SolutionTwo masses M and m are connected at the two ends of an inextensible string. The string passes over a smooth frictionless pulley. Calculate the acceleration of the masses and the tension in the string. Given M>m.
View Solution
Knowledge Check
Two masses (M+m)and(M−m) are attached to the ends of a light inextensible string and the string is made to pass over the surface of a smooth fixed pulley. When the masses are released from rest, the acceleration of the system is
Agm/MB2gM/mCgm/2MDg(M2−m2)/2MTwo bodies of masses 3kg and 2kg are connected by a long string and the string is made to pass over a smooth fixed pulley. Initially the bodies are held at the same level and released from rest. The velocity of the 3kg body after one second is (g=10ms2)
A2m/sB1m/sC0.4m/sD4m/sTwo blocks of masses 6kg and 4kg are attached to the two ends of a massless string passing over a smooth fixed pulley. if the system is released, the acceleration of the centre of mass of the system will be
Ag, vertically downwardsBg5, vertically downwardsCg25, vertically downwardsDzero
The masses (M+m) and (M−m) are attached to the ends of a light inextensible string and the string is made to pass over the surface of a smooth fixed pulley. When the masses are relased from rest the acceleraion of the system is .
View SolutionTwo bodies of masses 3kg and 2kg are connected by a along string and the string is made to pass over a smooth fixed pulley Initially the bodies are held at the saem level and released from rest. The velocity of the 3kg body after one second is (g=10m/s2) .
View SolutionTwo bodies of masses 4 kg and 6 kg are tied to the ends of a massless string. The string passes over a frictionless pulley. The acceleration of the system is :
View SolutionTwo bodies of masses m and M are attached to the two ends of a light string passing over a fixed ideal pulley (M>>m). When the bodies are in motion, the tension in the string is approximately
View SolutionTwo masses 2 kg and 3 kg are attached to the end of the string passed over a pulley fixed at the top. The tension and acceleration are
View Solution

