Question

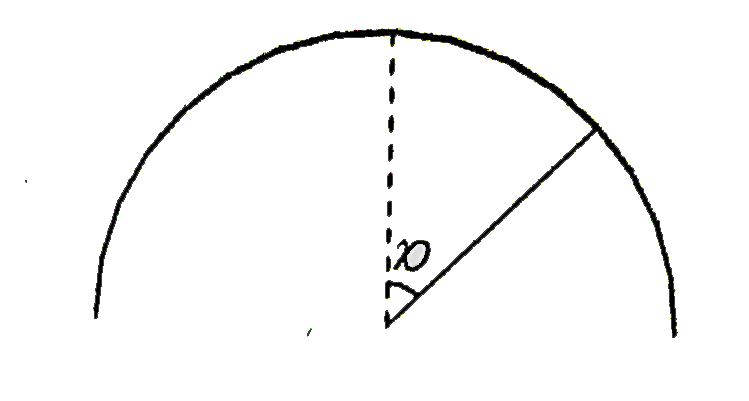
The coefficient of friction between a hemispherical bowl and an insect is $\sqrt{0.44}$ and the radius of the bowl is $0.6m$. The maximum height to which an insect can crawl in the bowl will be .

Options

A. `0.4m`
B. `0.2m`
C. `0.3m`
D. `0.1m`

Answer

D

Explanation

To find the maximum height to which an insect can crawl in a hemispherical bowl, we can follow these steps:

Step 1: Determine the coefficient of friction
Given that the coefficient of friction \( \mu = \sqrt{0.44} \).

Step 2: Calculate the angle of repose
The angle of repose \( \theta \) can be calculated using the formula:
\( \tan \theta = \frac{1}{\mu} \)
Substituting the value of \( \mu \):
\( \tan \theta = \frac{1}{\sqrt{0.44}} \)

Step 3: Calculate \( \sin \theta \)
Using the identity \( \sin^2 \theta + \cos^2 \theta = 1 \) and the relationship \( \tan \theta = \frac{\sin \theta}{\cos \theta} \), we can express \( \sin \theta \) in terms of \( \mu \):
\( \sin \theta = \frac{\mu}{\sqrt{1 + \mu^2}} \)
Substituting \( \mu = \sqrt{0.44} \):
\( \sin \theta = \frac{\sqrt{0.44}}{\sqrt{1 + 0.44}} = \frac{\sqrt{0.44}}{\sqrt{1.44}} = \frac{\sqrt{0.44}}{1.2} \)

Step 4: Calculate the height
The maximum height \( h \) to which the insect can crawl is given by:
\( h = r - r \sin \theta \)
Where \( r \) is the radius of the bowl (0.6 m). Thus:
\( h = r(1 - \sin \theta) = 0.6(1 - \frac{\sqrt{0.44}}{1.2}) \)

Step 5: Simplify the expression
Calculating \( \sqrt{0.44} \):
\( \sqrt{0.44} \approx 0.6633 \)
Now substituting back:
\( h = 0.6 \left( 1 - \frac{0.6633}{1.2} \right) = 0.6 \left( 1 - 0.55275 \right) = 0.6 \times 0.44725 \approx 0.26835 \)

Step 6: Final calculation
Thus, the maximum height \( h \) is approximately:
\( h \approx 0.26835 \text{ m} \)

Conclusion
The maximum height to which the insect can crawl in the bowl is approximately \( 0.26835 \text{ m} \).