Two bodies of masses 3kg and 2kg are connected by a along string and the string is made to pass over a smooth fixed pulley Initially the bodies are held at the saem level and released from rest. The velocity of the 3kg body after one second is (g=10m/s2) .
2m/s
1m/s
0.4m/s
4m/s
The correct Answer is:A
To solve the problem of finding the velocity of the 3 kg body after one second, we can follow these steps:
Step 1: Identify the masses and the gravitational acceleration
We have two masses:
- m1=3kg (the heavier mass)
- m2=2kg (the lighter mass)
The acceleration due to gravity is given as:
- g=10m/s2
Step 2: Determine the net force acting on the system
The net force acting on the system can be calculated using the difference in weights of the two masses. The force due to gravity on each mass is:
- Weight of m1=m1⋅g=3kg⋅10m/s2=30N
- Weight of m2=m2⋅g=2kg⋅10m/s2=20N
The net force F acting on the system is:
F=m1⋅g−m2⋅g=30N−20N=10N
Step 3: Calculate the total mass of the system
The total mass M of the system is the sum of the two masses:
M=m1+m2=3kg+2kg=5kg
Step 4: Calculate the acceleration of the system
Using Newton's second law, the acceleration a of the system can be calculated as:
a=FM=10N5kg=2m/s2
Step 5: Use the kinematic equation to find the velocity
Since the bodies are released from rest, the initial velocity u=0. We can use the kinematic equation:
v=u+at
where:
- v is the final velocity,
- u is the initial velocity (0 in this case),
- a is the acceleration (2 m/s²),
- t is the time (1 second).
Substituting the values:
v=0+(2m/s2)(1s)=2m/s
Final Answer
The velocity of the 3 kg body after one second is 2m/s.
---
We have two masses:
- m1=3kg (the heavier mass)
- m2=2kg (the lighter mass)
- g=10m/s2
The net force acting on the system can be calculated using the difference in weights of the two masses. The force due to gravity on each mass is:
- Weight of m1=m1⋅g=3kg⋅10m/s2=30N
- Weight of m2=m2⋅g=2kg⋅10m/s2=20N
F=m1⋅g−m2⋅g=30N−20N=10N
The total mass M of the system is the sum of the two masses:
M=m1+m2=3kg+2kg=5kg
Using Newton's second law, the acceleration a of the system can be calculated as:
a=FM=10N5kg=2m/s2
Since the bodies are released from rest, the initial velocity u=0. We can use the kinematic equation:
v=u+at
where:
- v is the final velocity,
- u is the initial velocity (0 in this case),
- a is the acceleration (2 m/s²),
- t is the time (1 second).
v=0+(2m/s2)(1s)=2m/s
The velocity of the 3 kg body after one second is 2m/s.
Topper's Solved these Questions
- NEWTONS LAWS OF MOTIONBook:NARAYNAChapter:NEWTONS LAWS OF MOTIONExercise:LEVEL -III
Explore 31 Videos
- NEWTONS LAWS OF MOTIONBook:NARAYNAChapter:NEWTONS LAWS OF MOTIONExercise:NCERT BASED QUESTION
Explore 33 Videos
- NEWTONS LAWS OF MOTIONBook:NARAYNAChapter:NEWTONS LAWS OF MOTIONExercise:LEVEL -I (C.W)
Explore 47 Videos
- MOTION IN A STRAIGHT LINEBook:NARAYNAChapter:MOTION IN A STRAIGHT LINEExercise:Level 2 H.W
Explore 29 Videos
- OSCILLATIONSBook:NARAYNAChapter:OSCILLATIONSExercise:EXERCISE - IV
Explore 41 Videos
Similar Questions
Two bodies of masses 11kg and 11.5kg are connected by a long light string passing over a smooth pulley Calculate velocity and height ascended/descended by each body at the end of 4s .
View SolutionTwo bodies of masses 4kg and 3kg respectively are connected by a light string passing over a smooth frictionless pulley Calculate the acceleration of the masses and tension in the string .
View Solution
Knowledge Check
Two bodies of masses 3kg and 2kg are connected by a long string and the string is made to pass over a smooth fixed pulley. Initially the bodies are held at the same level and released from rest. The velocity of the 3kg body after one second is (g=10ms2)
A2m/sB1m/sC0.4m/sD4m/sTwo blocks of masses of 40 kg and 30 kg are connected by a weightless string passing over a frictionless pulley as shown in the figure.
 A0.7ms−2B0.8ms−2C0.6ms−2D0.5ms−2
A0.7ms−2B0.8ms−2C0.6ms−2D0.5ms−2Two masses (M+m)and(M−m) are attached to the ends of a light inextensible string and the string is made to pass over the surface of a smooth fixed pulley. When the masses are released from rest, the acceleration of the system is
Agm/MB2gM/mCgm/2MDg(M2−m2)/2M
Two blocks of masses 2 kg and 1 kg respectively are tied to the ends of a string which passes over a light frictionless pulley . The masses are held at rest at the same horizontal level and then released . The distance traversed by centre of mass in 2 s is ( g = 10 m/s2)
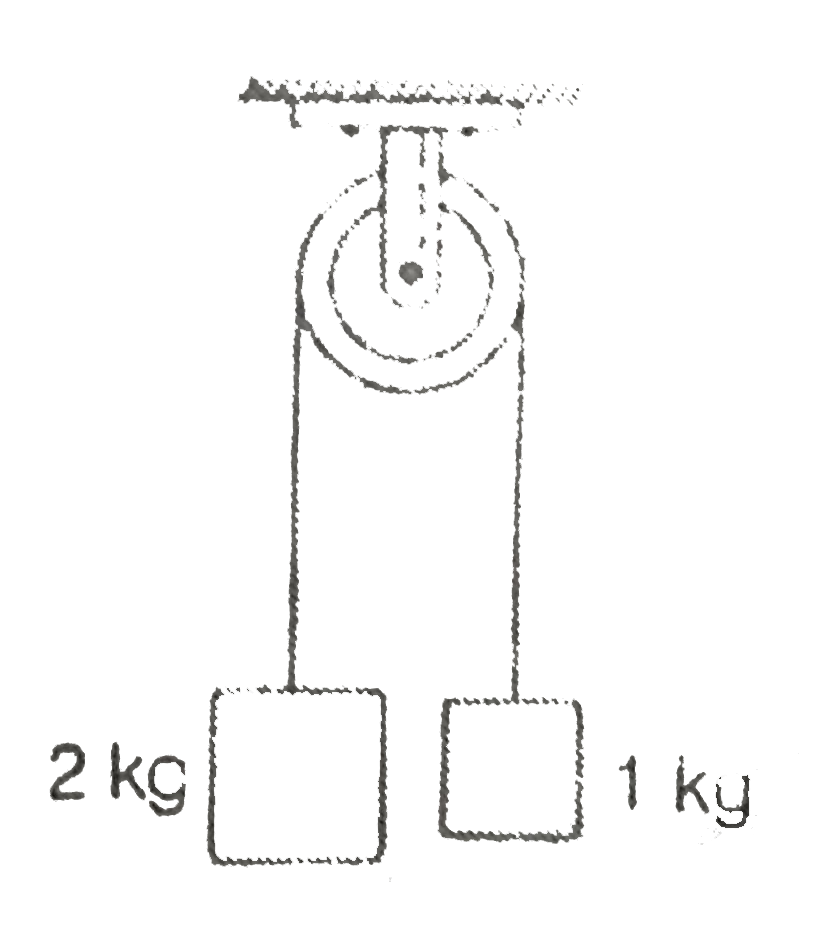
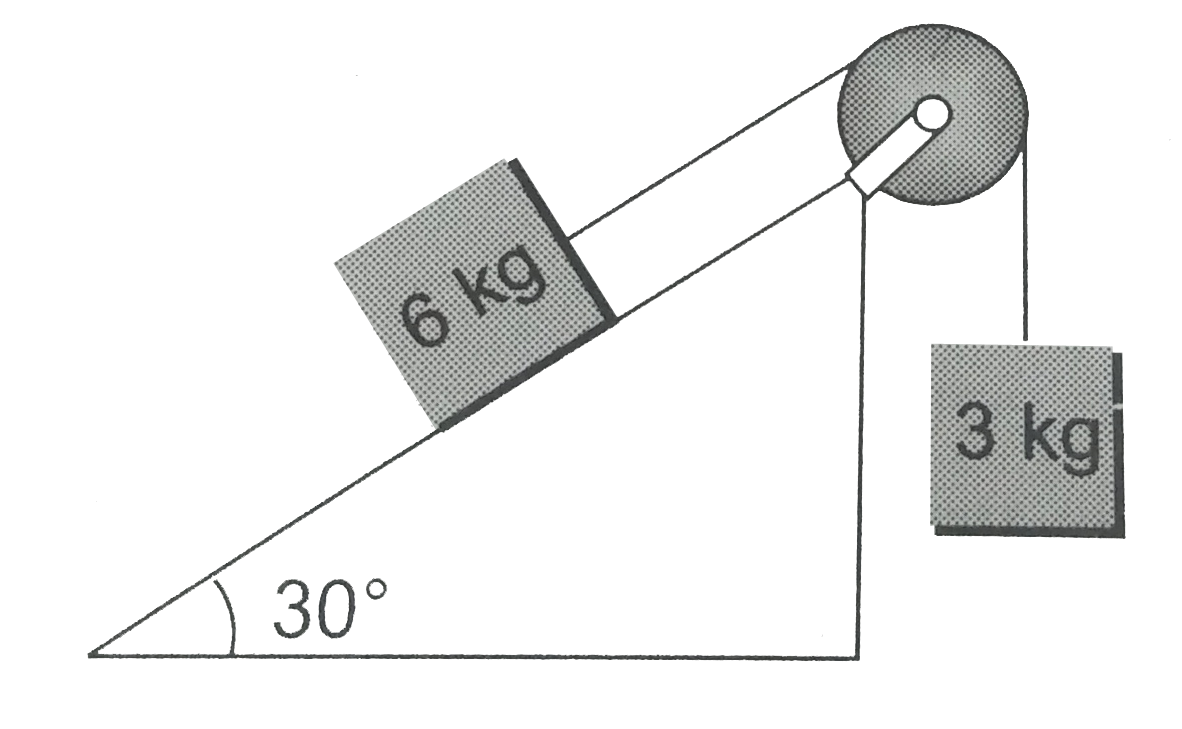
View SolutionTwo blocks of masses 3 kg and 6 kg are connected by a string as shown in the figure over a frictionless pulley. The acceleration of the system is
View SolutionTwo bodies of masses 4 kg and 6 kg are tied to the ends of a massless string. The string passes over a frictionless pulley. The acceleration of the system is :
View SolutionTwo bodies of masses 5kg and 4kg are tied to a string as shown. If the table and pulley are smooth, then acceleration of 5kg mass will be
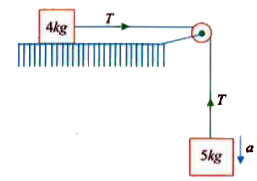
View SolutionTwo bodies of masses 5kg and 4kg are tied to a string as shown If the table and pulley are smooth, then acceleration of 5kg mass will be
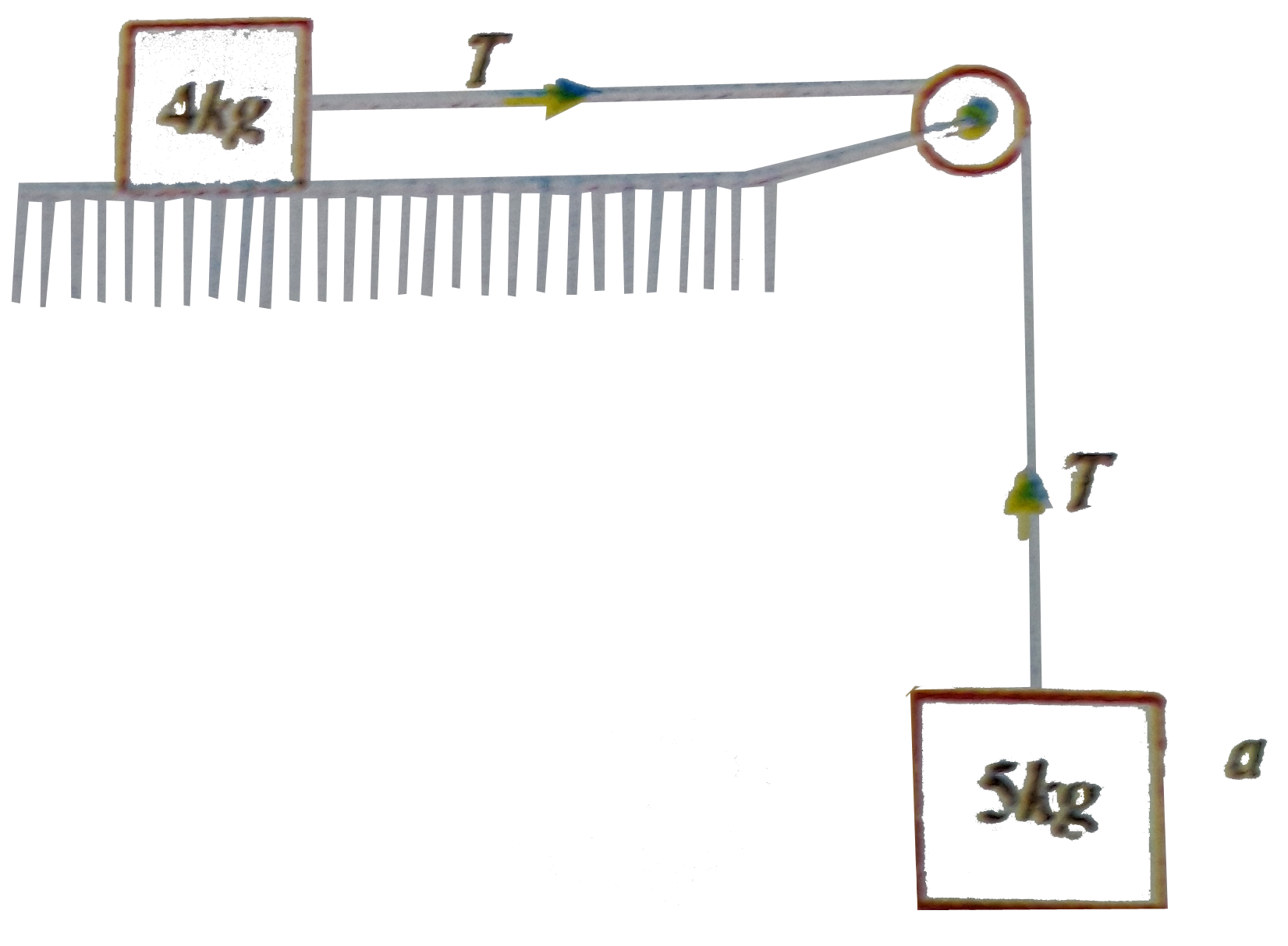 .
.
View Solution

