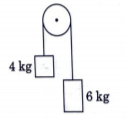
Two bodies of masses 4 kg and 6 kg are tied to the ends of a massless string. The string passes over a frictionless pulley. The acceleration of the system is :
g2
g3
g5
g10
The correct Answer is:C
To find the acceleration of the system with two masses (4 kg and 6 kg) connected by a string over a frictionless pulley, we can follow these steps:
Step 1: Identify the Forces Acting on Each Mass
- The mass m1=4kg will experience a gravitational force downward, which is Fg1=m1⋅g=4g.
- The mass m2=6kg will also experience a gravitational force downward, which is Fg2=m2⋅g=6g.
Step 2: Determine the Net Force Acting on the System
Since the 6 kg mass is heavier, it will accelerate downward, while the 4 kg mass will accelerate upward. The net force acting on the system can be calculated as:
Fnet=Fg2−Fg1=6g−4g=2g
Step 3: Calculate the Total Mass of the System
The total mass mtotal of the system is the sum of the two masses:
mtotal=m1+m2=4kg+6kg=10kg
Step 4: Apply Newton's Second Law
According to Newton's second law, the acceleration a of the system can be found using the formula:
Fnet=mtotal⋅a
Substituting the values we have:
2g=10a
Step 5: Solve for Acceleration
To find a, we rearrange the equation:
a=2g10=g5
Final Answer
Thus, the acceleration of the system is:
a=g5m/s2
- The mass m1=4kg will experience a gravitational force downward, which is Fg1=m1⋅g=4g.
- The mass m2=6kg will also experience a gravitational force downward, which is Fg2=m2⋅g=6g.
Since the 6 kg mass is heavier, it will accelerate downward, while the 4 kg mass will accelerate upward. The net force acting on the system can be calculated as:
Fnet=Fg2−Fg1=6g−4g=2g
The total mass mtotal of the system is the sum of the two masses:
mtotal=m1+m2=4kg+6kg=10kg
According to Newton's second law, the acceleration a of the system can be found using the formula:
Fnet=mtotal⋅a
Substituting the values we have:
2g=10a
To find a, we rearrange the equation:
a=2g10=g5
Thus, the acceleration of the system is:
a=g5m/s2
Similar Questions
Two bodies of mass 4 kg and tied to the ends of a massless string. the string passes over a pully which is frictionless (see figure). the acceleration of the system in terms of acceleration due to gravity (g) is:
View SolutionTwo masses 8 kg and 12 kg are connected at the two ends of a light inextensible string that passes over a frictionless pulley Fibd the acceleration of the masses and tension in the string , when the masses are released
 .
.
View Solution
Knowledge Check
Two bodies of mass 4 kg and tied to the ends of a massless string. the string passes over a pully which is frictionless (see figure). the acceleration of the system in terms of acceleration due to gravity (g) is:
 Ag/2Bg/5Cg/10Dg
Ag/2Bg/5Cg/10DgTwo bodies of mass 3 kg and 4 kg are suspended at the ends of massless string passing over a frictionless pulley. The acceleration of the system is (g=9.8m/s2)
A4.9m/s2B2.45m/s2C1.4m/s2D9.5m/s2Two bodies of mass 5 kg and 7 kg are suspended at the ends of massless string passing over frictionless pulley. The acceleration of the system.
A1.6m/s2B10m/s2C9.8m/s2D7m/s2
Two masses 7 kg and 12 kg are connected at the two ends of a light inetensible string that goes over a frictionless pulley. Find the acceleration of the masses and the tension in the string when the masses are released.
View SolutionTwo bodies of mass 3kg and 4kg are suspended at the ends of massless string passing over a frictionless pulley. The acceleration of the system is (g=9.8m/s2)
View SolutionTwo bodies of massless string passing over a frictionless pulley. The acceleration of the system is (g=9.8m/s2)
View SolutionTwo blocks of masses 3 kg and 6 kg are connected by a string as shown in the figure over a frictionless pulley. The acceleration of the system is

View SolutionTwo spheres of masses 3 kg and 4 kg are attached to ends of a string which passes over a frictionless pulley. Take g=9.8m/2. The relative acceleration of the system is
View Solution

