A circuit consists of a source of a constant and a resistance amd a capacitor with capacitance connected in series. The internal resistance of the source is negligible. At a moment the capacitance of the capacitor is abruply decreased -fold. FInd the current flowing through the circuit as a function of time .
Suppose is the charge at the time , Initially , at .
Then at time .
But, (-sign because charge decreases)
So
or,
, from at
Hence,
Finally,

Topper's Solved these Questions
- ELECTRODYNAMICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:ELECTRODYNAMICSExercise:Constant Magnetic Fiels - Magnetics
Explore 69 Videos
- ELECTRODYNAMICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:ELECTRODYNAMICSExercise:Electromagnetic Induction
Explore 84 Videos
- ELECTRODYNAMICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:ELECTRODYNAMICSExercise:Electric Capacitance - Energy Of An Electric Field
Explore 46 Videos
- ELECTRICITY AND MAGNETISMBook:IE IRODOV, LA SENA & SS KROTOVChapter:ELECTRICITY AND MAGNETISMExercise:All Questions
Explore 6 Videos
- ELECTROMAGNETISMBook:IE IRODOV, LA SENA & SS KROTOVChapter:ELECTROMAGNETISMExercise:All Questions
Explore 24 Videos
Similar Questions
A closed circuit consits of a source of constant and E and a choke coil of inductance L connected in series. The active resistance of the whole circuit is equal to R. At the moment t=0 the choke coil inductance was decreased abrupty η times. FInd the current in the circuit as a function of time t.
View SolutionA closed circuit consists of a source of constant emfE and a choke coil of inductance L connected in series.The active resistance of the whole circuit is equal to R.It is in steady state.At the moment L=0 the choke coil inductance was decreased abruptly 4 times.The current in the circuit as a function of time t is ER[1−xc−4tR/L].Find out value of x.
View Solution
Knowledge Check
circuit consists of a source of EMF ξ and internal resistance r, two capacitors each of capacitance C and two resistors, each of value R. The voltage across either capacitor is:
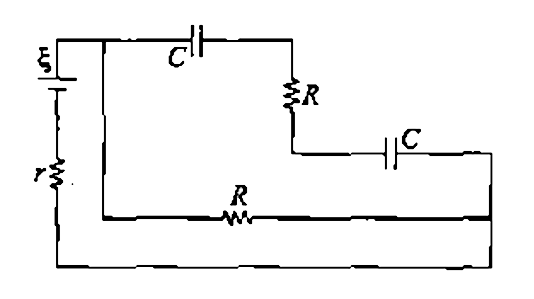 AξR2(R+r)BξR(R+r)Cξ(R+r)2RDZero
AξR2(R+r)BξR(R+r)Cξ(R+r)2RDZeroA capacitor of capacitance 20μF is connected in series with 25Ω resistance to 240 V, 50 Hz AC. The maximum current in the circuit is
A14.9 AB1.49 AC2.49 AD2.89 AAn AC circuit consists of an inductor of inductance 0.5H and a capacitor of capacitance 8μF in series. The current in the circuit is maximum when the angular frequency of AC source is
A500rad/secB2×105rad/secC4000rad/secD5000rad/sec
A circuit consisting of a capacitor with capacitance C and a resistance R connected in series was connected at the moment t=0 to a source of ac voltage V=Vmcosωt . Find the current in the circuit as a function of time t.
View SolutionA circuit consists of a capacitor with capacitance C and a coil of inductance L connected in series, as well as a switch and a resistance equal to the critical value for this circuit. With the switch disconnected, the capacitor was charged to a voltage V0, and at the moment t=0, the switch was closed . Find the corrent I in the circuit as a function of time t.What is Imax equal to ?
View SolutionA circuit consists of a capacitor with capacitance C and a coil with active resistance R and inductance L connected in parallel. Find the impedane of the circuit at frequency ω of alternating voltage.
View SolutionAn a.c.source is connected to a capacitor of capacitance C. Find the expression for current flowing through it.
View SolutionAn a.c. circuit consists of an inductor of inductance 0.5 H and a capacitor of capacitance 8 uF in series. The current in the circuit is maximum when the angular frequency of a.c. source is
View Solution

