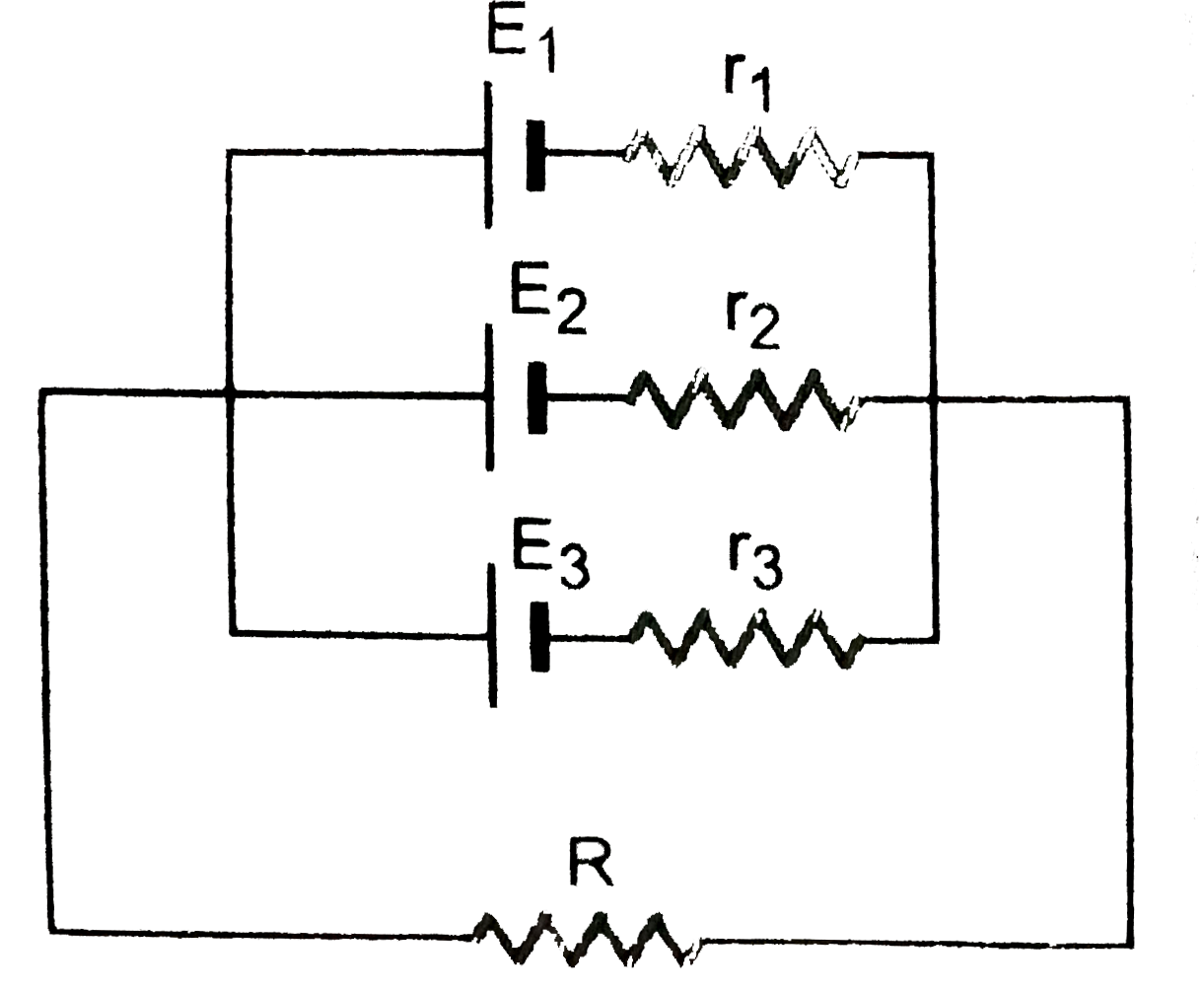
Find the emf and the internal resistance of a source which is equivalent to two batteries connected in parallel whose emf's are equal to E1 and E2 and internal resistances to R1 and R2
Let us connect a load of resistance R between the points A and B (fig)
From the loop rule, Δφ=0, we obtains
iR=ξ1−i1R1....(1)
and iR=ξ2−(i−i1)R2
or i(R+R2)=ξ+i1R2 ....(2)
Solving Eqs. (1) and (2), we get
i=ξ1R1+ξ2R2R1+R2/R+R1R2R1+R2=ξoR+R0 ....(3)
where ξ0=ξ1R1+ξ2R2R1+R2 and R0=R1R2R1+R2
Thus one can replace the given arrangement of the cells by a single cell having the emf ξ0 and internal resistance R0.

Topper's Solved these Questions
- ELECTRODYNAMICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRODYNAMICSEXERCISE - Constant Magnetic Fiels - Magnetics
69 Videos
- ELECTRODYNAMICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRODYNAMICSEXERCISE - Electromagnetic Induction
84 Videos
- ELECTRODYNAMICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRODYNAMICSEXERCISE - Electric Capacitance - Energy Of An Electric Field
46 Videos
- ELECTRICITY AND MAGNETISMBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRICITY AND MAGNETISMEXERCISE - All Questions
6 Videos
- ELECTROMAGNETISMBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTROMAGNETISMEXERCISE - All Questions
24 Videos
Similar Questions
Find the emf ε and the internal resistance r of an electric source which is equivalent to two batteries of emf's ε1 and ε2 and internal resistances r1andr2, connected in parallel.
View SolutionFind the emf (V) and internal resistance (r) of a single battery which is equivalent to a parallel combination of two batteries of emf's V1,andV_(2), and internal resistance r1 and r2 respectively, with polarities as shown in the figure
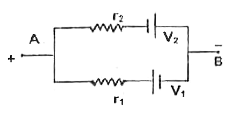
View Solution
Knowledge Check
Six cell each of emf E and internal resistance r are connected in series. If due to over sight, two cells are connected wrongly, then the equivalent emf and internal resistance of the combination is
A6E,6rB4E,6rC2E,6rD2E,4rIf n cells each of emf E and internal resistance are connected in parallel, then the total emf and internal resistances will be
Aε,rnBε,nrCnε,rnDnε,nrFive cells each of emf E and internal resistance r are connected in series. Due to oversight one cell is connected wrongly . The equivalent emf and internal resistance of the combination is
A3E,3rB5E , 3rC3E, 5rD5E,5r
Find the e.m.f(E0) end internal resistance (r0) of a simple battery which is equivalent to a perallel combination of two battery of e.m.fE1andE2 and internal resistance v1andv2 respectively with polarities
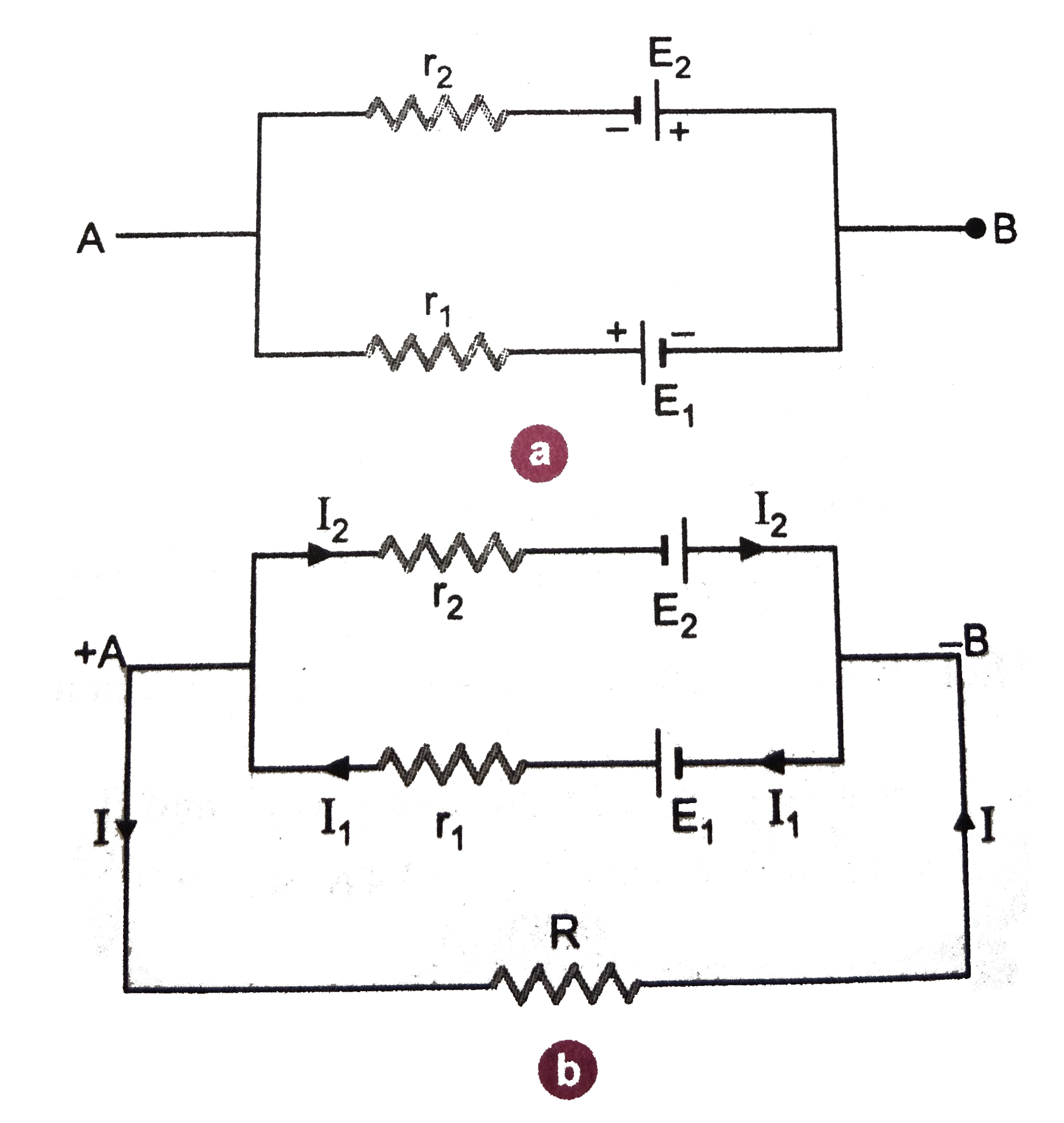
View Solution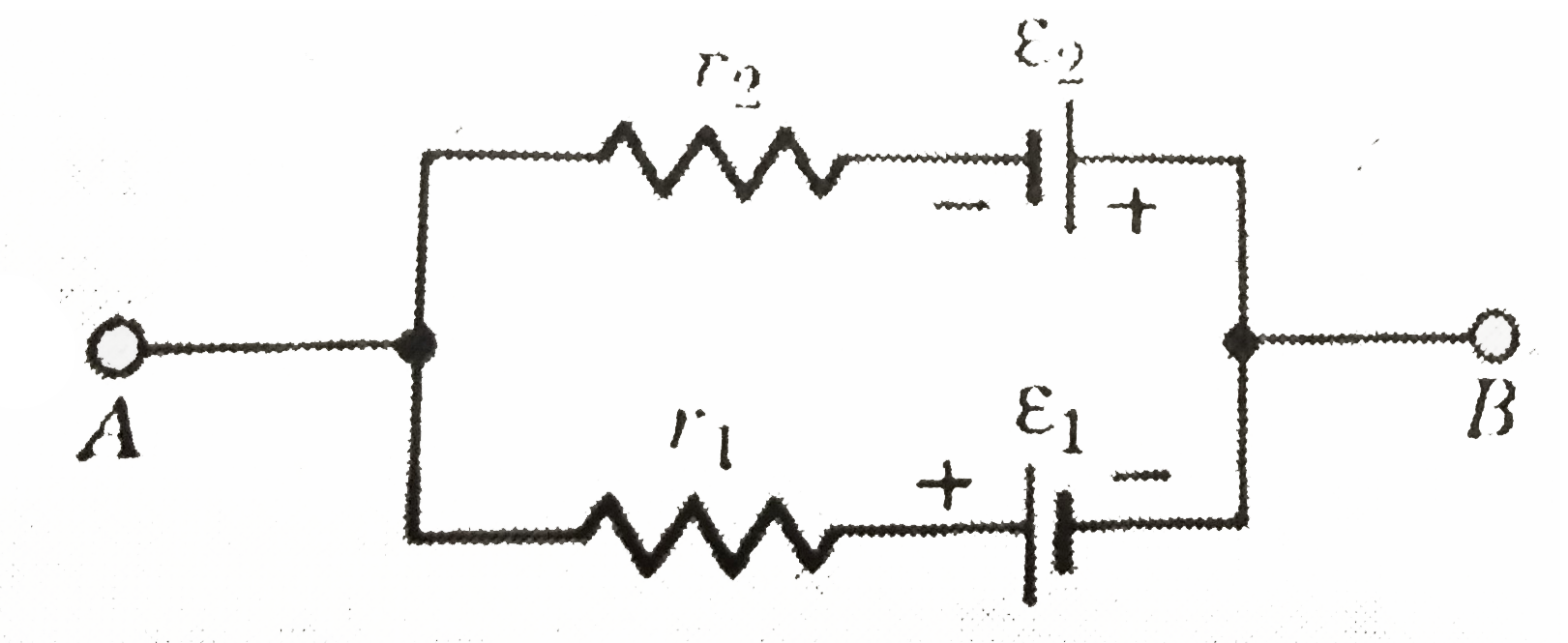
find the emf (ε0) and internal resistance (r0) if a battery which is equivalent to a parallel combination of two batteries of emfs ε1andε2 and internal resistances r1andr2 respectively, with polarities as shown in figure.
View SolutionFind the emf (V) and internal resistance (R) of a single battery which is equivalent toa parallel combination of two batteries of emf V1 and V2 and internal resistances r1 and r2 respectively, with polrities as shown in figure
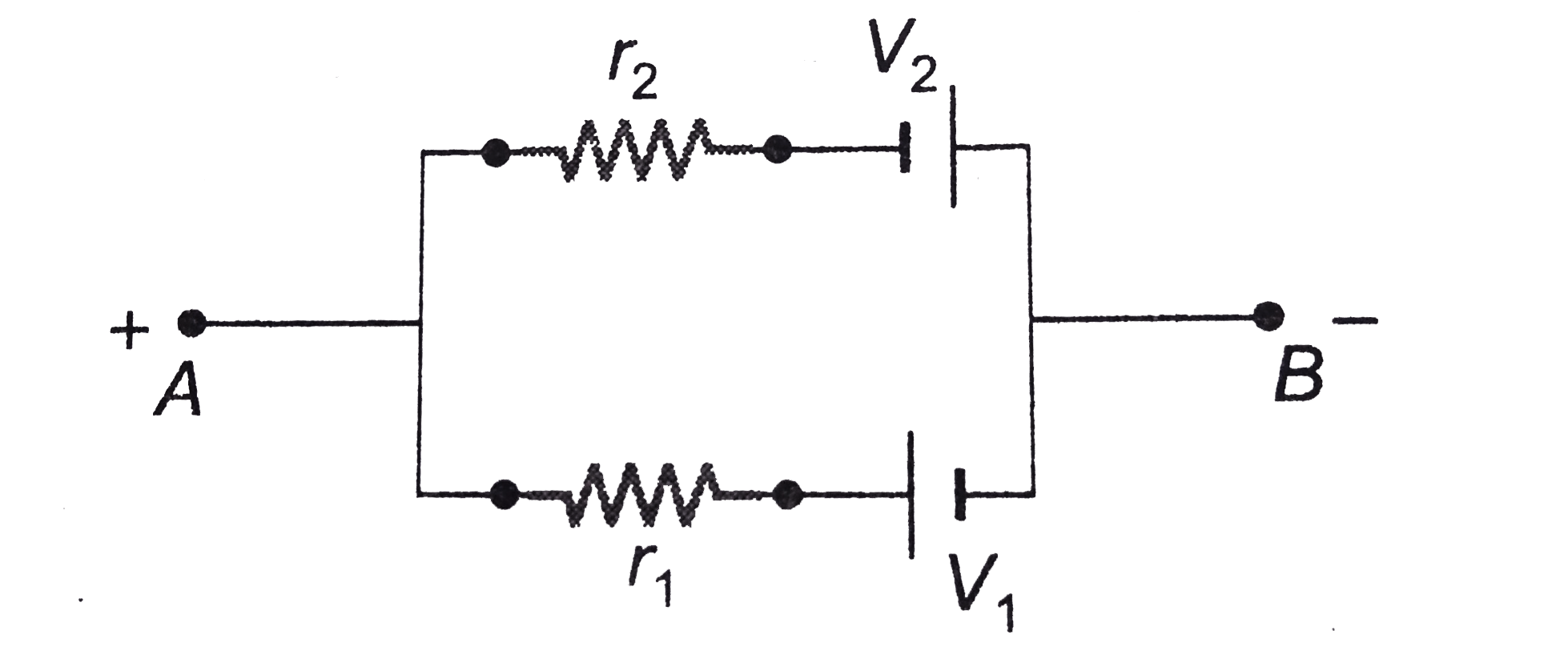
View SolutionIf three cell are connected in parallel then equivalent emf……. and equivalent internal resistance is …..
View SolutionTwo cells of emf 2ε and ε and internal resistance 2r and r respectively, are connected in parallel. Obtain the expressions for the equivalent emf and the internal resistance of the combination.
View Solution
