Find the emf (V) and internal resistance (r) of a single battery which is equivalent to a parallel combination of two batteries of emf's V1,andV_(2), and internal resistance r1 and r2 respectively, with polarities as shown in the figure

V1r2−V2r1r1+r2, r1r2r1+r2
Topper's Solved these Questions
- CURRENT ELECTRICITYBook:FIITJEEChapter:CURRENT ELECTRICITYExercise:ASSIGNMENT PROBLEMS (OBJECTIVE)(Level-1)
Explore 45 Videos
- CURRENT ELECTRICITYBook:FIITJEEChapter:CURRENT ELECTRICITYExercise:ASSIGNMENT PROBLEMS (OBJECTIVE)(Level-II)
Explore 20 Videos
- CURRENT ELECTRICITYBook:FIITJEEChapter:CURRENT ELECTRICITYExercise:ASSIGNMENT PROBLEMS (SUBJECTIVE)(Level-1)
Explore 15 Videos
- COLLISION Book:FIITJEEChapter:COLLISION Exercise:(NUMERICAL BASED QUESTIONS)
Explore 4 Videos
- ELASTICITY AND WAVES Book:FIITJEEChapter:ELASTICITY AND WAVES Exercise:Assignment Problems (Objective) Level-II
Explore 15 Videos
Similar Questions
Find the emf (V) and internal resistance (R) of a single battery which is equivalent toa parallel combination of two batteries of emf V1 and V2 and internal resistances r1 and r2 respectively, with polrities as shown in figure

View Solution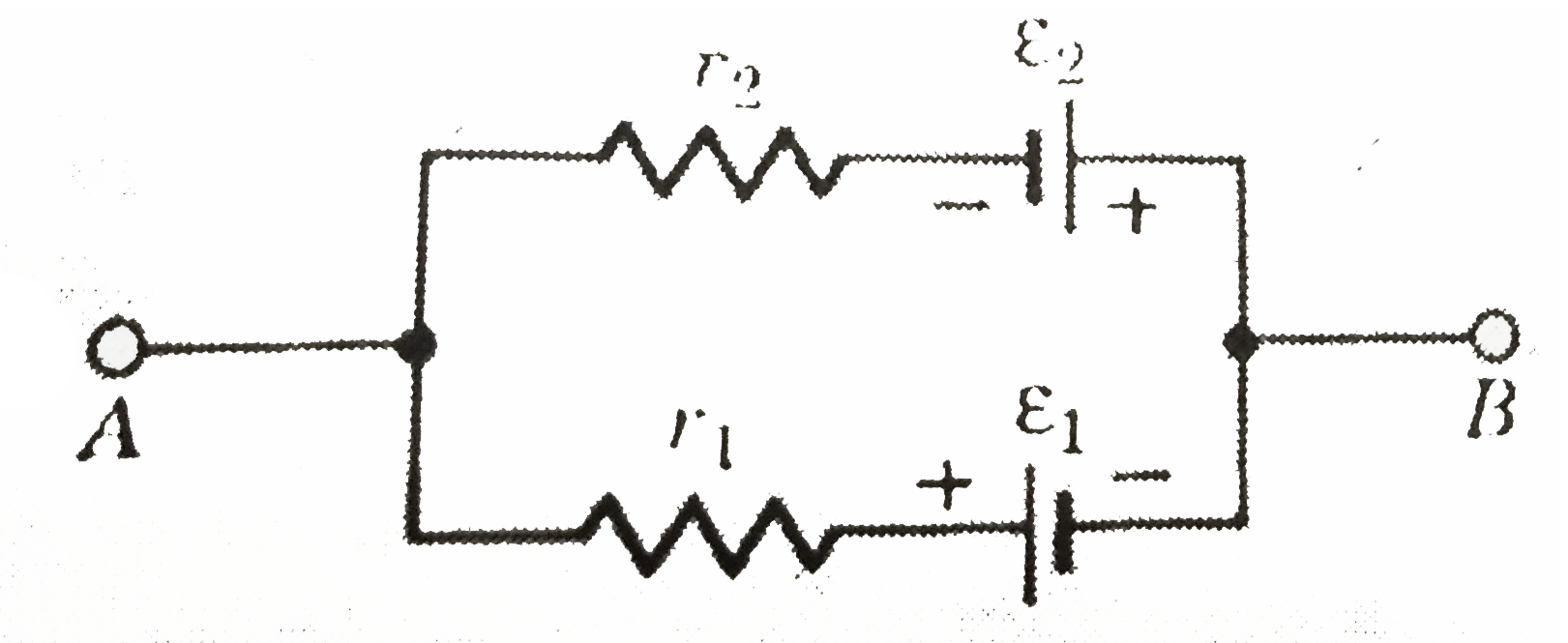
find the emf (ε0) and internal resistance (r0) if a battery which is equivalent to a parallel combination of two batteries of emfs ε1andε2 and internal resistances r1andr2 respectively, with polarities as shown in figure.
View Solution
Knowledge Check
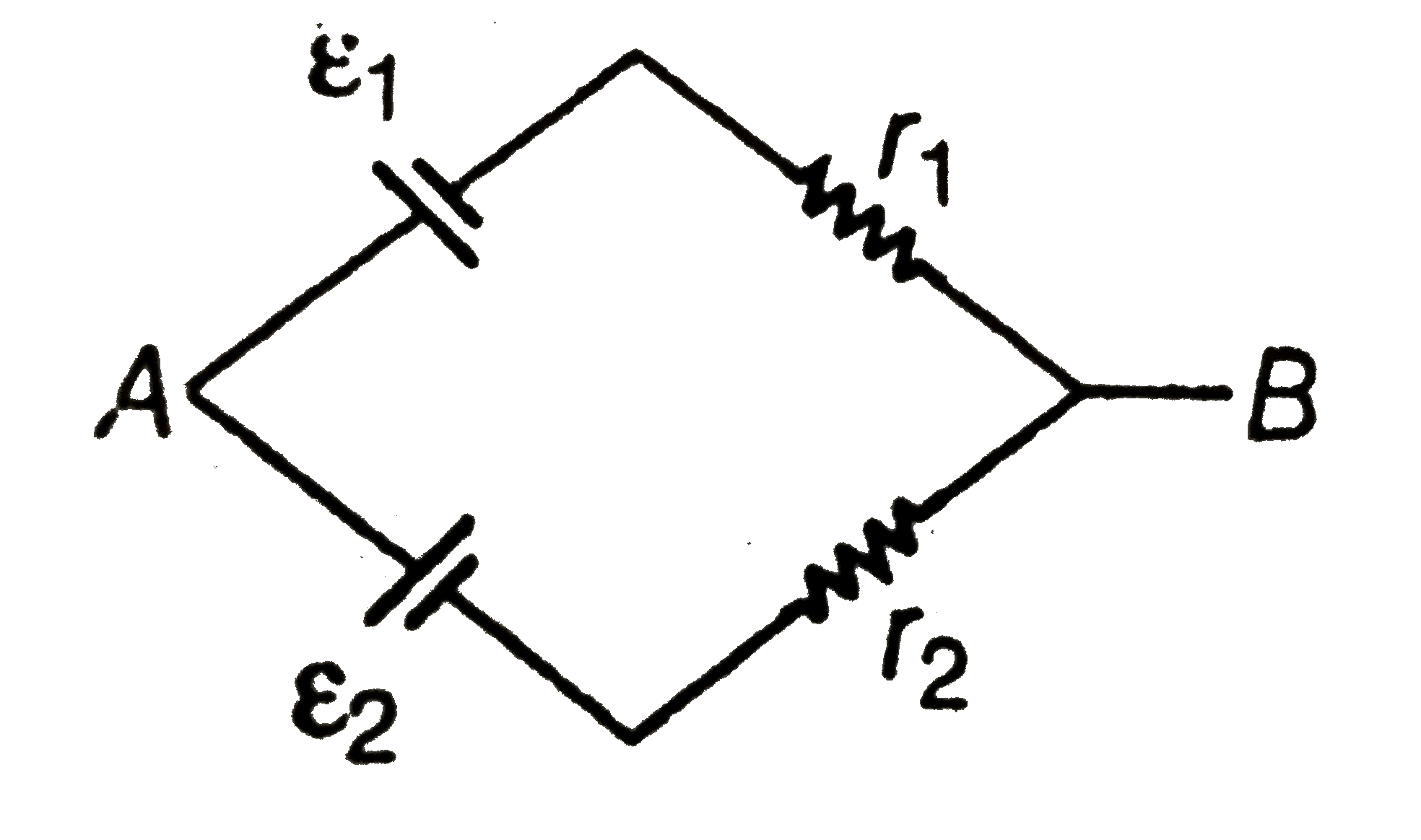
Two batteries of emf ε1andε2(ε2>ε1) and internal resistance r1andr2 respectively are connected in parallel as shown in figure.AThe equivalent emf εeq of the two cells is between ε1andε2, i.e., ε1<εeq<ε2Bthe equivalent emf εeq is smaller than ε1CThe εeq is given by εeq=ε1+ε2 always.Dεeq is independent of internal resistance r1andr2.Two batteris of emf ε1 and ε2 wit respective internal resistance r1 and r2 are connected in parallel. Now
AThe effective emf of this parallel combination is (ε1r1+ε2r2)(r1+r2)BThe effective internal resistance of this combination is 2r1r2(r1+r2)Cthe effective emf of this parallel combination is (ε1r2+ε2r1)(r1+r2)DThe effective internal resistance of this combination is r1r2(r1+r2)Two batteries of emf ε1 and ε2(ε2>ε1) and internal resistances r_1 and r2 respectively are connected in parallel as shown in Fig. Then
 Athe equivalent emf εeq of the two cells is betweenε1 and ε2 i.e., ε1<εeq<ε2Bthe equivalent emf εeq is smaller than ε1Cthe εeq is given by εeq=ε1+ε2 always .Dεeq is independent of internal resistances r1 and r2
Athe equivalent emf εeq of the two cells is betweenε1 and ε2 i.e., ε1<εeq<ε2Bthe equivalent emf εeq is smaller than ε1Cthe εeq is given by εeq=ε1+ε2 always .Dεeq is independent of internal resistances r1 and r2
Find the e.m.f(E0) end internal resistance (r0) of a simple battery which is equivalent to a perallel combination of two battery of e.m.fE1andE2 and internal resistance v1andv2 respectively with polarities
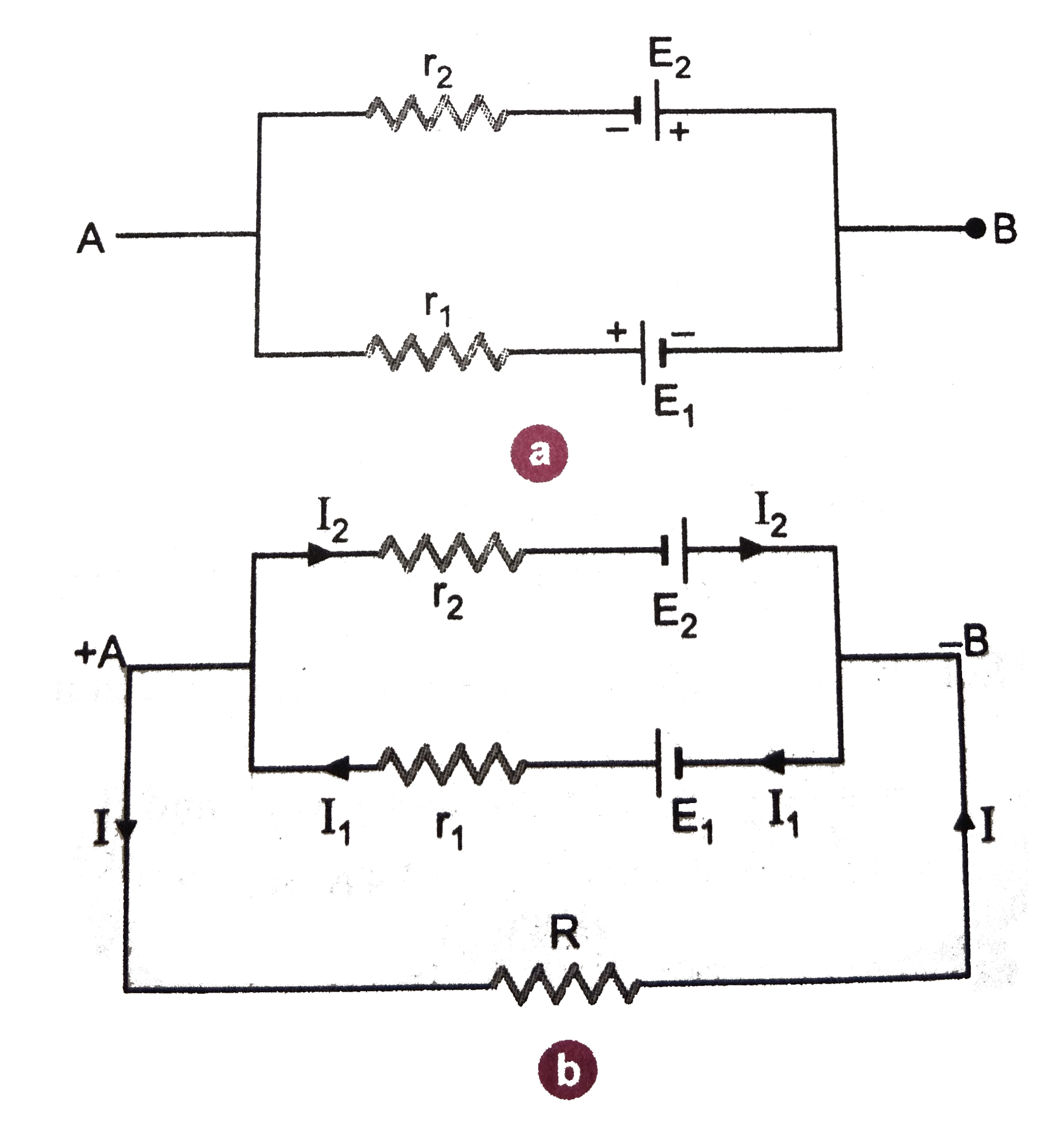
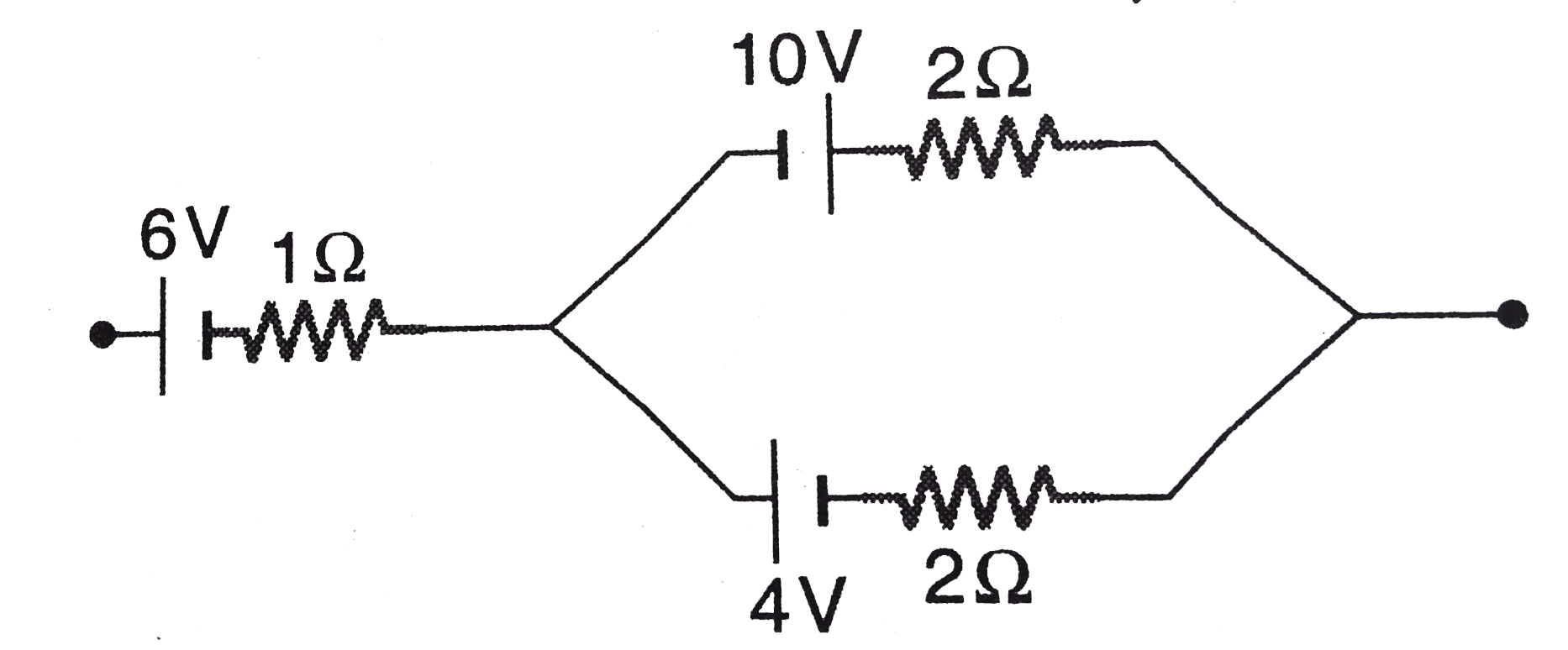
View SolutionFind the emf and internal resistance of a single battery which is equivalent to a combination of three batteries as show in figure.
View SolutionFind the emf ε and the internal resistance r of an electric source which is equivalent to two batteries of emf's ε1 and ε2 and internal resistances r1andr2, connected in parallel.
View SolutionFind the emf and the internal resistance of a source which is equivalent to two batteries connected in parallel whose emf's are equal to E1 and E2 and internal resistances to R1 and R2
View SolutionTwo batteries of e.m.f. E1 and E2 and internal resistance r1 and r2 are connected in parallel. Determine their equivelent e.m.f.
View Solution

