A conductor has a temperature-independent resistance R and a total heat capacity C. At the momenet t=0 it is connected to a dc voltage V. Find the time dependence of a conductor's temperature T assuming the thermal power dissipated into surrounding space to very as q=k(T−T0), where k is constant, T0 is the enviroment temperature (equal to the conductor's temperature at the initial moment).
The equaction of heat balance is
V2R−k(T−T0)=CdTdt
Put T−T0=ξ
So, Cξ+kξ=V2R or, ξ+kCξ=V2CR
or, ddt(ξekt/c)=V2CReky/c
or, ξekt/c=V2kRekt/c+A
where A is a constant Clearly
ξ=0 at t=0, so A=V2kR and hence,
T=T0+V2kR(1−e−kt/C)
Topper's Solved these Questions
- ELECTRODYNAMICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:ELECTRODYNAMICSExercise:Constant Magnetic Fiels - Magnetics
Explore 69 Videos
- ELECTRODYNAMICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:ELECTRODYNAMICSExercise:Electromagnetic Induction
Explore 84 Videos
- ELECTRODYNAMICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:ELECTRODYNAMICSExercise:Electric Capacitance - Energy Of An Electric Field
Explore 46 Videos
- ELECTRICITY AND MAGNETISMBook:IE IRODOV, LA SENA & SS KROTOVChapter:ELECTRICITY AND MAGNETISMExercise:All Questions
Explore 6 Videos
- ELECTROMAGNETISMBook:IE IRODOV, LA SENA & SS KROTOVChapter:ELECTROMAGNETISMExercise:All Questions
Explore 24 Videos
Similar Questions
A conductor has a temperature independent resistance R and a total heat capacity C. At the moment t=0 it is connected to a DC voltage V. Find the times dependence of the conductors temperature t assuming the thermal power dissipated into surrounding space to vary as q=k(T−T0) where k is a constant T0 is the surrounding temperature (equal to conductor's temperature at the initial moment).
View SolutionA conductor is at T kelvin. Find the thermal speed of free electrons of the conductor .
View Solution
Knowledge Check
V=k(PT)0.33 where k is constant. It is an,
Aisothermal processBadiabatic processCisochoric processDisobaric processA metal piece is heated up to T K. The temperature of the surrounding is t K. The heat lost to the surrounding due to radiation is proportional to
AT4−t4B(T−t)4CT4+t4D(T+t)4A metal piece is heated up to T K. The temperature of the surrounding is t K. The heat lost to the surrounding due to radiation is proportional to
AT4−t4B(T−t4)C(T4+t4)D(T4+t4)
Show that the velocity of sound in a gas is given by vt=v0+(v0/546)t, where v0 is the velocity at 0∘C and t is the temperature of the gas in ∘C. Assume t<<273.
View SolutionA metal piece is heated up to T K. The temperature of the surrounding is t K. The heat lost to the surrounding due to radiation is proportional to
View Solution
Two ends of a rod of uniform cross sectional area are kept at temperature 3T0 and T0 as shown. Thermal conductivity of rod varies as k=αT, (where α is a constant and T is absolute temperature). In steady state, the temperature of the middle section of the rod is
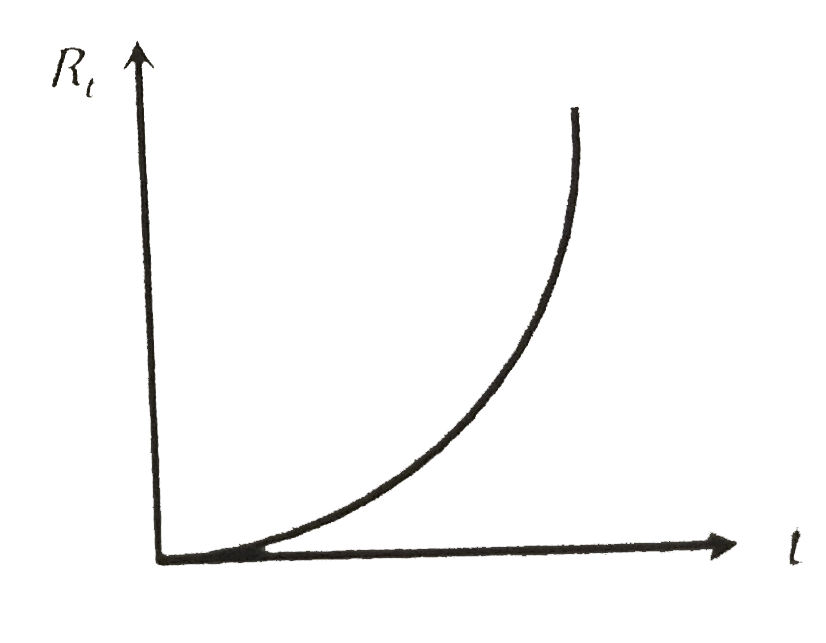
View SolutionThe resistance t R of a conductor varies with temperature t as shown in the figure. If the variation is represented by Rt=R0[1+αt+βt2], then
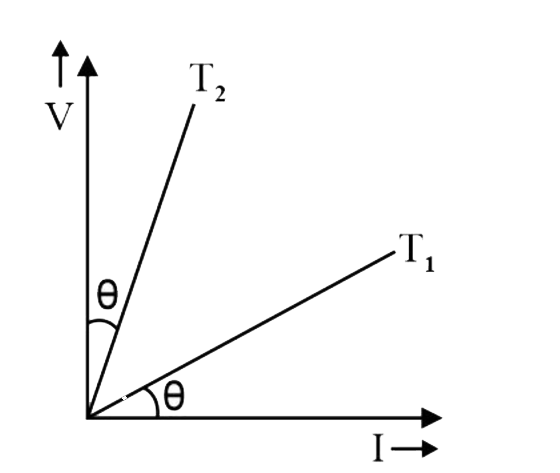
View SolutionThe V - I graphs for a conductor at temperature T1andT2 are shown in the figure (T2−T1) is proportional to
View Solution

