The radii of spherical capacitor electrodes are equal to a and b, with a<b. The interlectordes ε and resistivity ρ. Inititally the capacitor is not charged. At the moment t=0 the internal electorde gets a charge q0 Find:
(a) the times variation of the charge on the internal elecrtordes,
(b) the amount of the heat generated during the spreading of the charge.
(a) Let us mentally isolatate a thin spherical layer with inner and outer radii r and r+dr respective. Lince of current at all the points of this layer are perpendicular to it and therefore such a layer can be treated as a spherical conductor of thickness dr and cross sectional area 4πr3. Now we know that resistance,
dR=ρdrS(r)=ρdr4πr2 ....(1)
Intergating expression (1) between teh Hints,
∫R0dR=∫bRρdr4πr2 or, R=ρ4π[1a−1b] ......(2)
Capacitance of the network, C=4πε0ε[1a−1b] ......(3)
and q=Cφ [where q is the charge at any arbitary moment] ....(4)
also, φ=(−dqdt)Ras capacitor is discharging, ....(5)
From Eqs.(2), (3),(4) and (5) we get,
q=4πε0ε[1a−1b][−dqdt]ρ[1a−1b]4π or, dqq=dtρεε0
Intergating ∫qq0−dqq=1ρε0ε∫t0dt=dtρεε0
Hence q=q0e−tρε0ε
(b) From energy conservation heat generated,m during the spreading of the charge,
H=Ui−Uf [because Acell=0]
=12q204πε0ε[1a−1b]−0=q208πε0εonb−aab
Topper's Solved these Questions
- ELECTRODYNAMICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRODYNAMICSEXERCISE - Constant Magnetic Fiels - Magnetics
69 Videos
- ELECTRODYNAMICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRODYNAMICSEXERCISE - Electromagnetic Induction
84 Videos
- ELECTRODYNAMICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRODYNAMICSEXERCISE - Electric Capacitance - Energy Of An Electric Field
46 Videos
- ELECTRICITY AND MAGNETISMBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRICITY AND MAGNETISMEXERCISE - All Questions
6 Videos
- ELECTROMAGNETISMBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTROMAGNETISMEXERCISE - All Questions
24 Videos
Similar Questions
Knowledge Check
At t<0, the capacitor is charged and the switch is opened.At t=0 the switch is closed.The shortest time T at which the charge on the capacitor will be zero is given by:
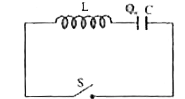 Aπ√LCB32π√LCCπ2√LCD2π√LC
Aπ√LCB32π√LCCπ2√LCD2π√LCA capacitor of 4μF is connected as shwon in the figure. The internal resistance of the battery is 0.5Ω. The amount of charge on the capacitor plates will be
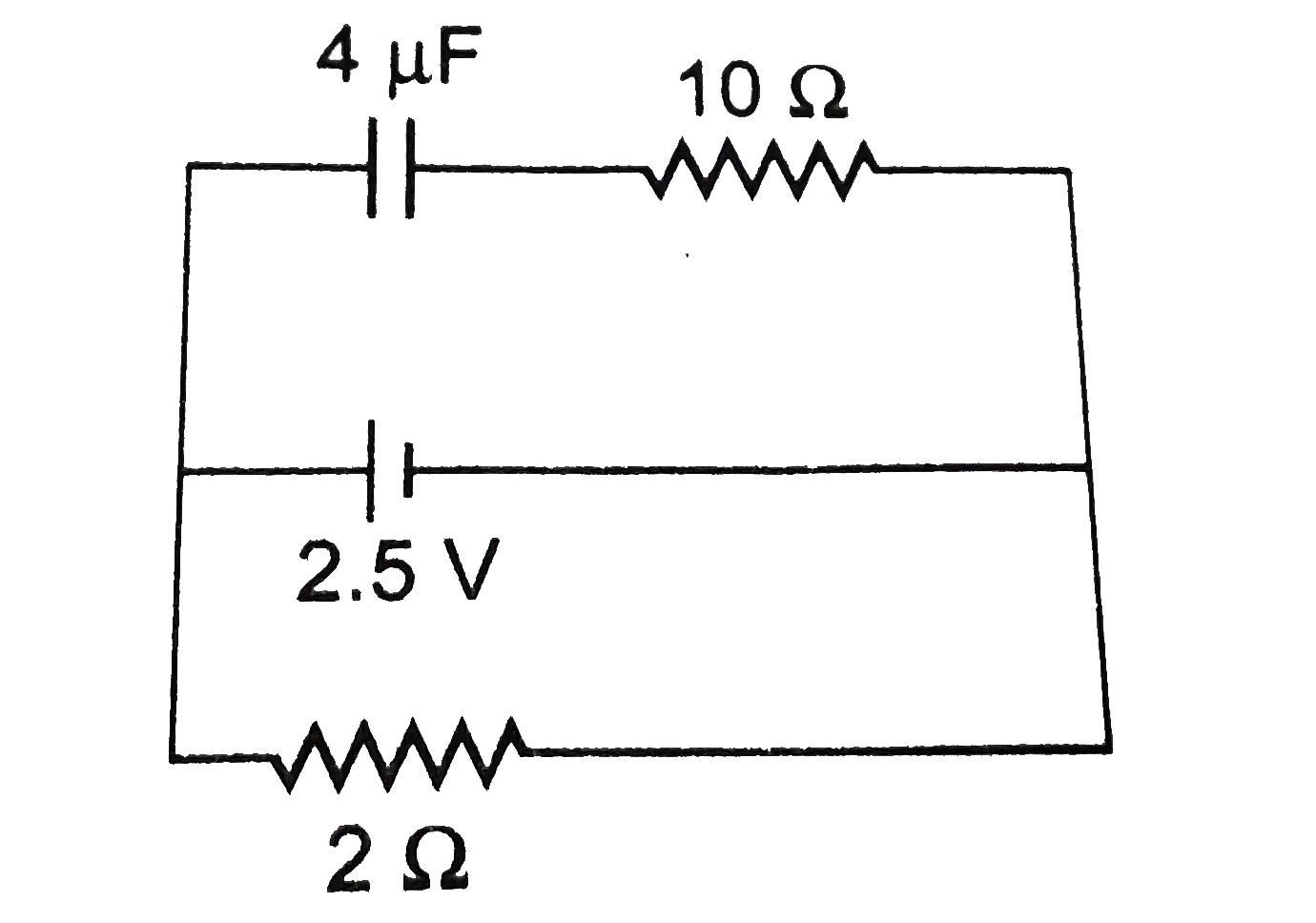 A0B4μCC16μCD8μC
A0B4μCC16μCD8μC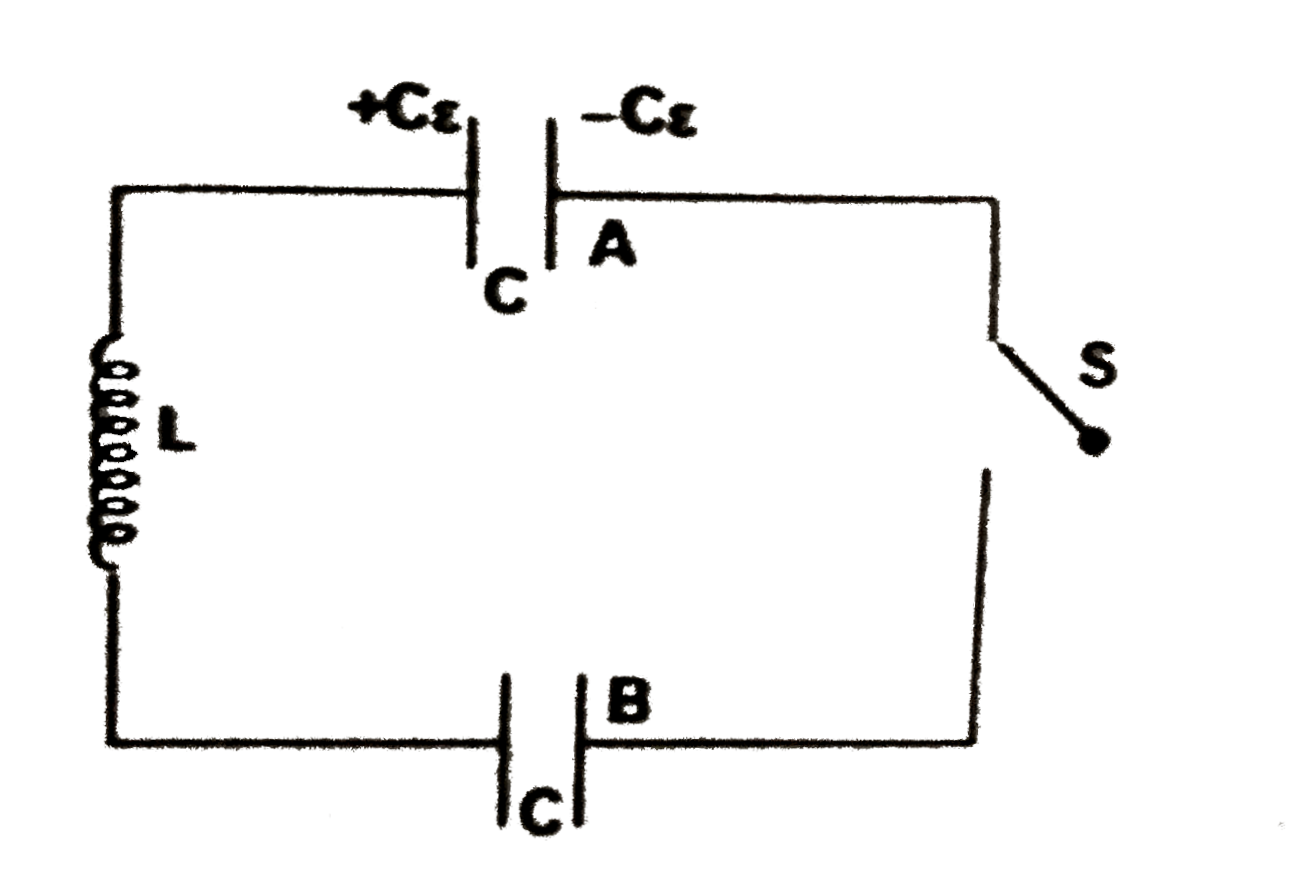
Initially capacitor 'A' is charged to a potential drop ε and capacitor B is uncharged At t=0, switch S is closed, then the maximum current through the inductor isAε√C2LBε√CLC2ε(CL)Dε2√CL
Initially the capacitor is uncharged find the charge on capacitor as a function of time, if switch is closed at t=0.

View Solution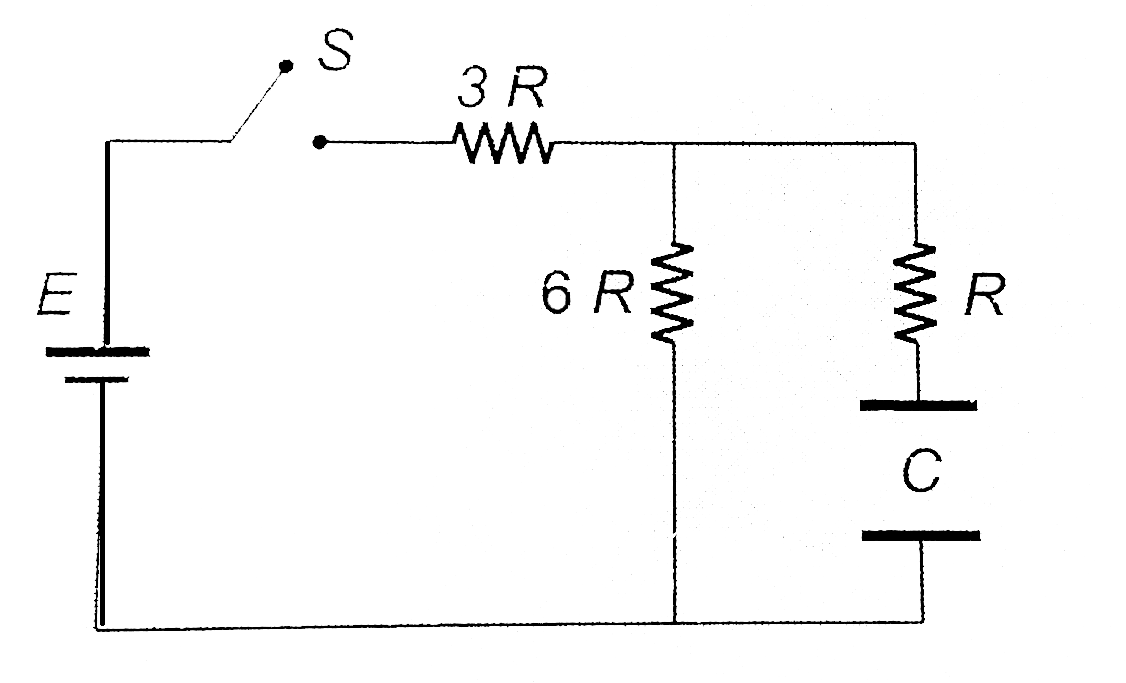
Find (a) equivalent time constant, (b) charge on capacitor in terms of time t.
View SolutionA capacitor of capacitance C is given a charge Q. At t=0,it is connected to an uncharged of equal capacitance through a resistance R. Find the charge on the second capacitor as a function of time.
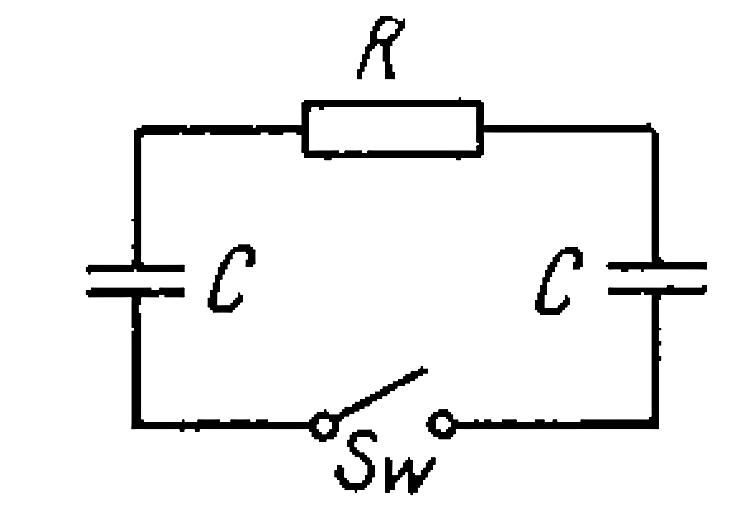
View SolutionIn a circuit shown in fig. the capacitance of each capacitor is equal to C and the resistance, to R One of the capacitor was connected to a voltage V0 and then at the moment t=0 was shorted by means of the swich Sw. Find:
(a) a current I in the circuit as a function of time t:
(b) the amount of generated heat provided a dependence I(t) is known.
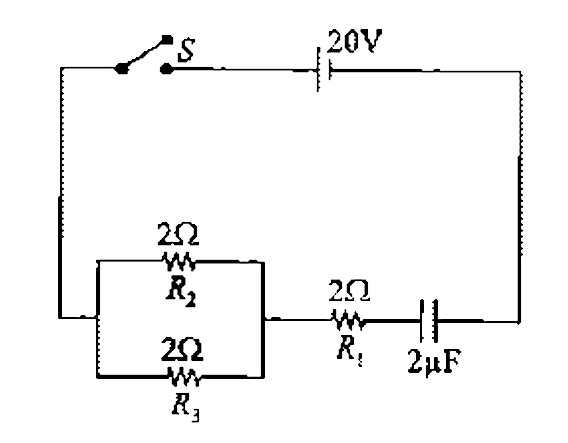
View SolutionThe circuit shown in figure-3.343 is closed at t=0. Calculate the total amount of heat generated in R2 during the time capacitor gets fully charged :
View Solution