A conductor has a temperature independent resistance R and a total heat capacity C. At the moment t=0 it is connected to a DC voltage V. Find the times dependence of the conductors temperature t assuming the thermal power dissipated into surrounding space to vary as q=k(T−T0) where k is a constant T0 is the surrounding temperature (equal to conductor's temperature at the initial moment).
The correct Answer is:A, B, C
V2R=k(T−T0)+C(dTdt)
or dTV2R−k(T−T0)=dtC
or∫TT0dTV2R−k(T−T0)=∫10dtC
(at t=0 temperature of conductor T=T0)
Solving this equation we get
T=T0+V2kR(1−e−kt/C)
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - DC PANDEYCHAPTER - CURRENT ELECTRICITYEXERCISE - Example
61 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEYCHAPTER - CURRENT ELECTRICITYEXERCISE - Check point
70 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEYCHAPTER - CURRENT ELECTRICITYEXERCISE - Level 2 Comprehension Example Type
2 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEYCHAPTER - COMMUNICATION SYSTEMEXERCISE - Subjective
11 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Medical entrances gallery
25 Videos
Similar Questions
A conductor has a temperature-independent resistance R and a total heat capacity C. At the momenet t=0 it is connected to a dc voltage V. Find the time dependence of a conductor's temperature T assuming the thermal power dissipated into surrounding space to very as q=k(T−T0), where k is constant, T0 is the enviroment temperature (equal to the conductor's temperature at the initial moment).
View SolutionThe temperature T of a cooling object drops at a rate proportional to the difference T−S where S is constant temperature of surrounding medium. If initially T=150∘C; find the temperature of the cooling object at any time t.
View Solution
Knowledge Check
A metal piece is heated up to T K. The temperature of the surrounding is t K. The heat lost to the surrounding due to radiation is proportional to
AT4−t4B(T−t)4CT4+t4D(T+t)4A metal piece is heated up to T K. The temperature of the surrounding is t K. The heat lost to the surrounding due to radiation is proportional to
AT4−t4B(T−t4)C(T4+t4)D(T4+t4)A metal piece is heated up to T K. The temperature of the surrounding is t K. The heat lost to the surrounding due to radiation is proportional to
AT4−t4B(T−t)4CT4+t4D(T+t)4
A circuit consisting of a capacitor with capacitance C and a resistance R connected in series was connected at the moment t=0 to a source of ac voltage V=Vmcosωt . Find the current in the circuit as a function of time t.
View SolutionA cylindrical conductor has a resistance R. When the conductor is at a temperature (T) above its surrounding temperature (T0), the ratio of thermal power dissipated by the conductor to its excess temperature (ΔT=T–T0) above surrounding is a known constant k. The conductor is connected to a cell of emf V. Initially, the conductor was at room temperature T0. Mass and specific heat capacity of the conductor are m and s respectively.
(i) find the time (t) dependence of the temperature (T) of the conductor after it is connected to the cell. Assume no change in resistance due to temperature.
(ii) find the temperature of the conductor after a long time.
View Solution
Two ends of a rod of uniform cross sectional area are kept at temperature 3T0 and T0 as shown. Thermal conductivity of rod varies as k=αT, (where α is a constant and T is absolute temperature). In steady state, the temperature of the middle section of the rod is
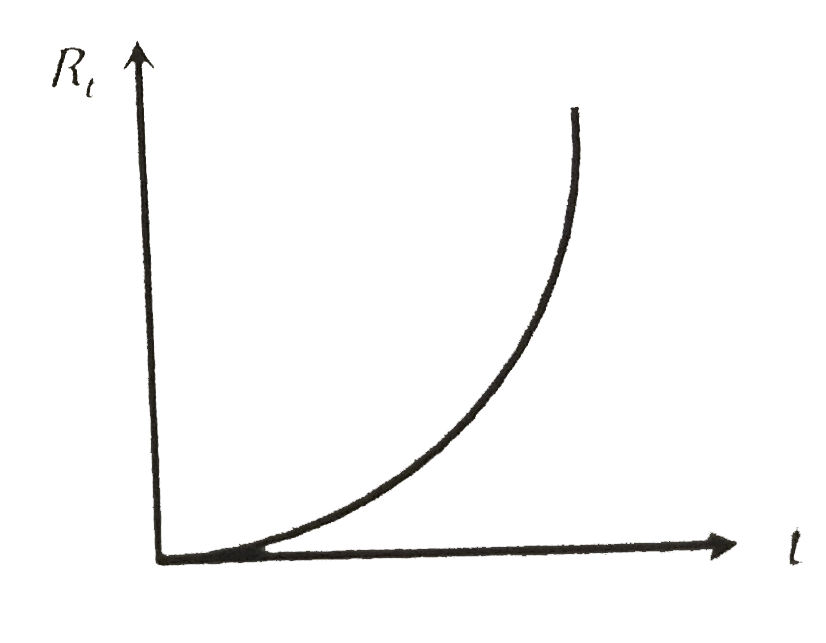
View SolutionThe resistance t R of a conductor varies with temperature t as shown in the figure. If the variation is represented by Rt=R0[1+αt+βt2], then
View SolutionA heated object (at time t=0 and temperature T=T0) is taken out of the oven to cool and placed on a table near an open window Write an expression for its temperature as function of time T where Ts is the surrounding temperature .
View Solution
