A heated object (at time t=0 and temperature T=T(0)) is taken out of t

If a piece of metal is heated to temperature $θ$ and the allowed to cool in a room which is at temperature $θ_{0}$ , the graph between the temperature T of the metal and time t will be closet to
A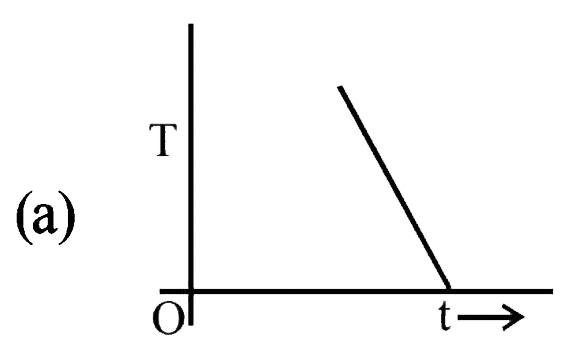
B
C
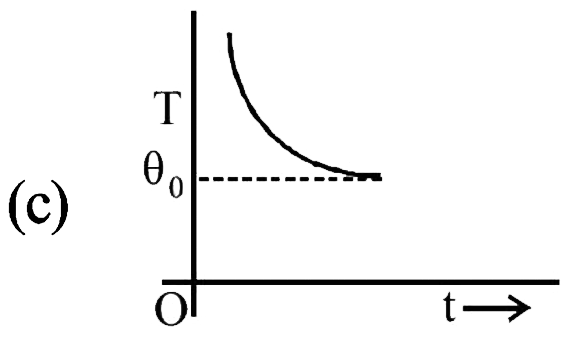D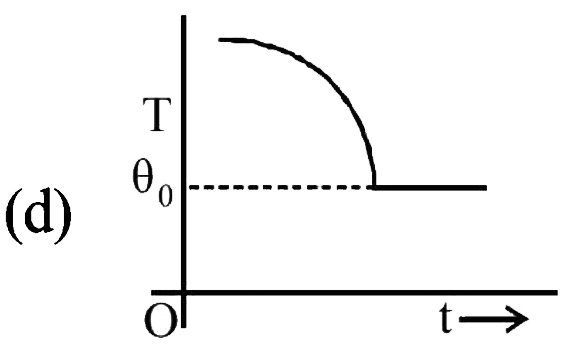
Two identical objects A and B are at temperature $T_{A}$ and $T_{B}$ respectively. Both objects are placed in a room with perfectly absorbing walls maintained at temperature $T (T_{A} > T > T_{B})$ .
Statement-1: The objects A and B attain the temperature T eventually
Statement-2: A only emits radiation while B only absorbs until radiation both attain the temperature T
AStatement-1 is true, statement-2 is true and statement-2 is correct explanation for statement-1.
BStatement-1 is true, statement-2 is true and statement-2 is NOT the correct explanation for statement-1.
CStatement-1 is true, statement-2 is false.
DStatement -1 is false, statement -2 is true.
The graph shows the variation of $l n R v / s \frac{1}{T^{2}}$ , where $R$ is resistance and $T$ is temperature. Then find $R$ as function $T$ .
A $R - R_{0} e_{0_{2}^{2 / T_{2}}}^{T_{0_{2}^{2 / T_{2}}}^{2 / T_{2}}}$
B $R - R_{0} e^{- T_{0^{2}}^{2 / T_{0^{2}}^{2}}}$
C $R - R_{0} e^{T_{0}^{3 / T_{0}}}$
D $R - R_{0} e^{- T_{0^{3}}^{3 / T_{0^{3}}^{3}}}$

A heated object (at time $t = 0$ and temperature $T = T_{0})$ is taken out of the oven to cool and placed on a table near an open window Write an expression for its temperature as function of time $T$ where $T_{s}$ is the surrounding temperature .