A liquid in a beaker has temperature at time t and is temperature of surroundings, then according to Newton's law of cooling the correct graph between and t is :
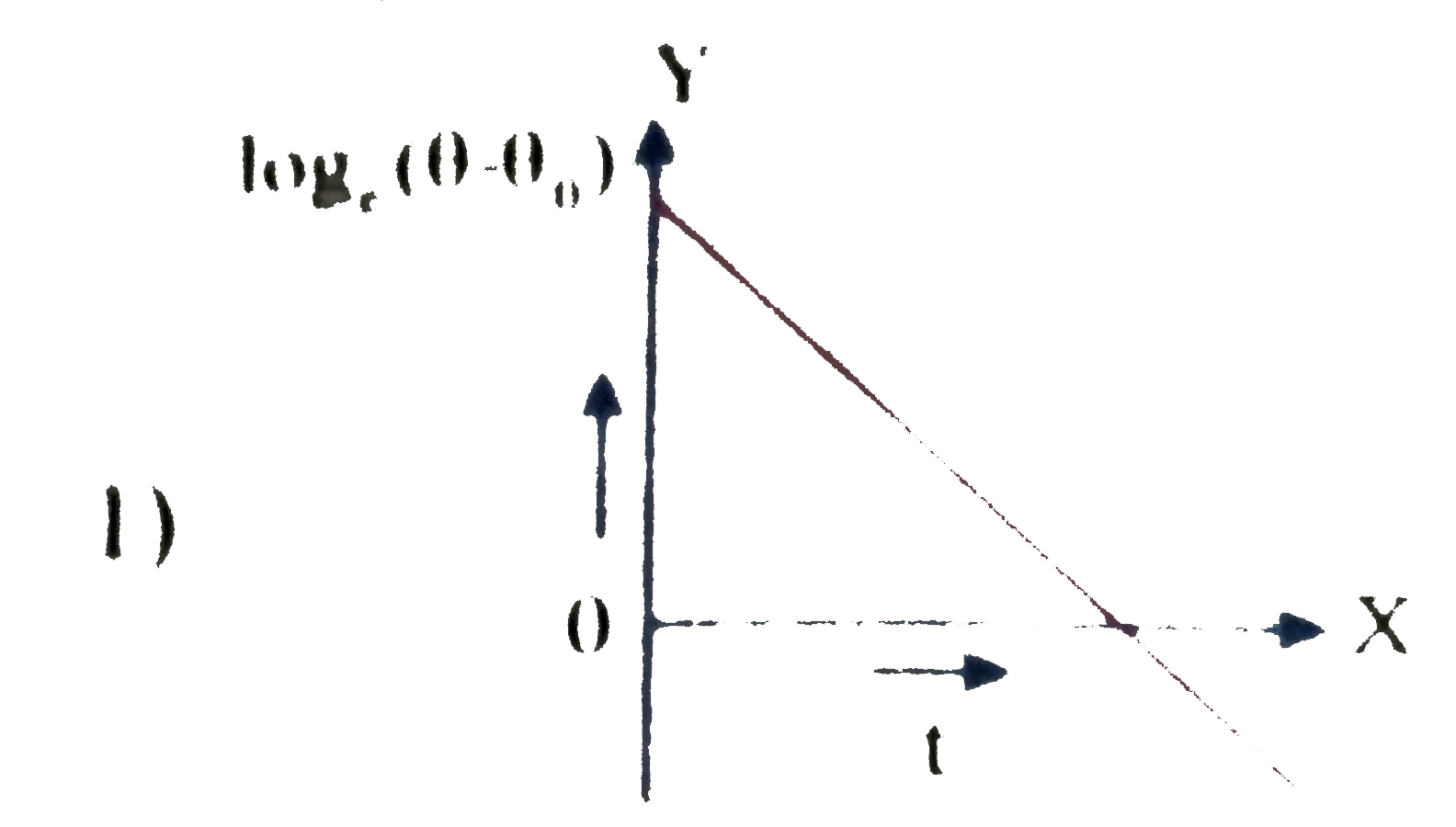
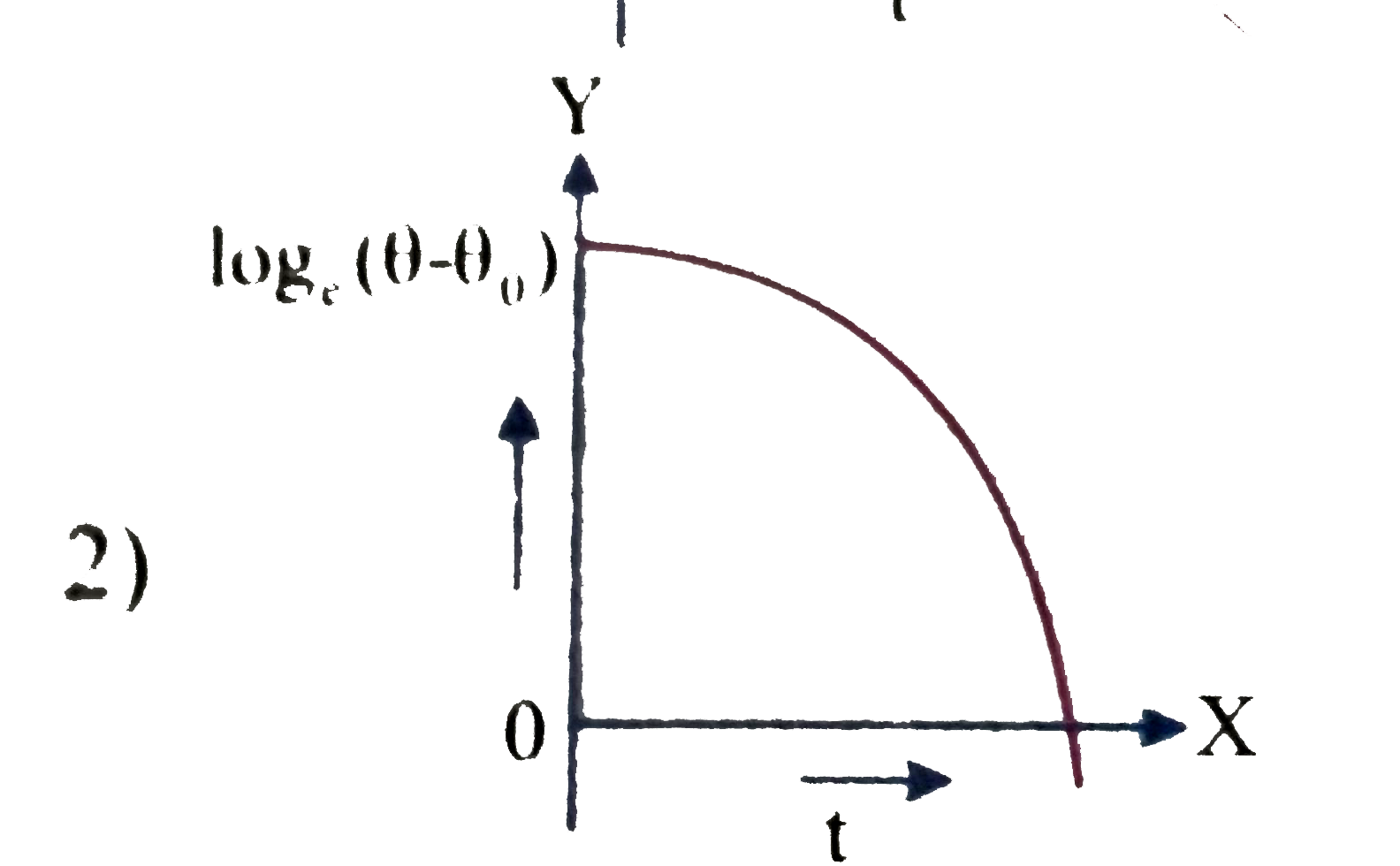
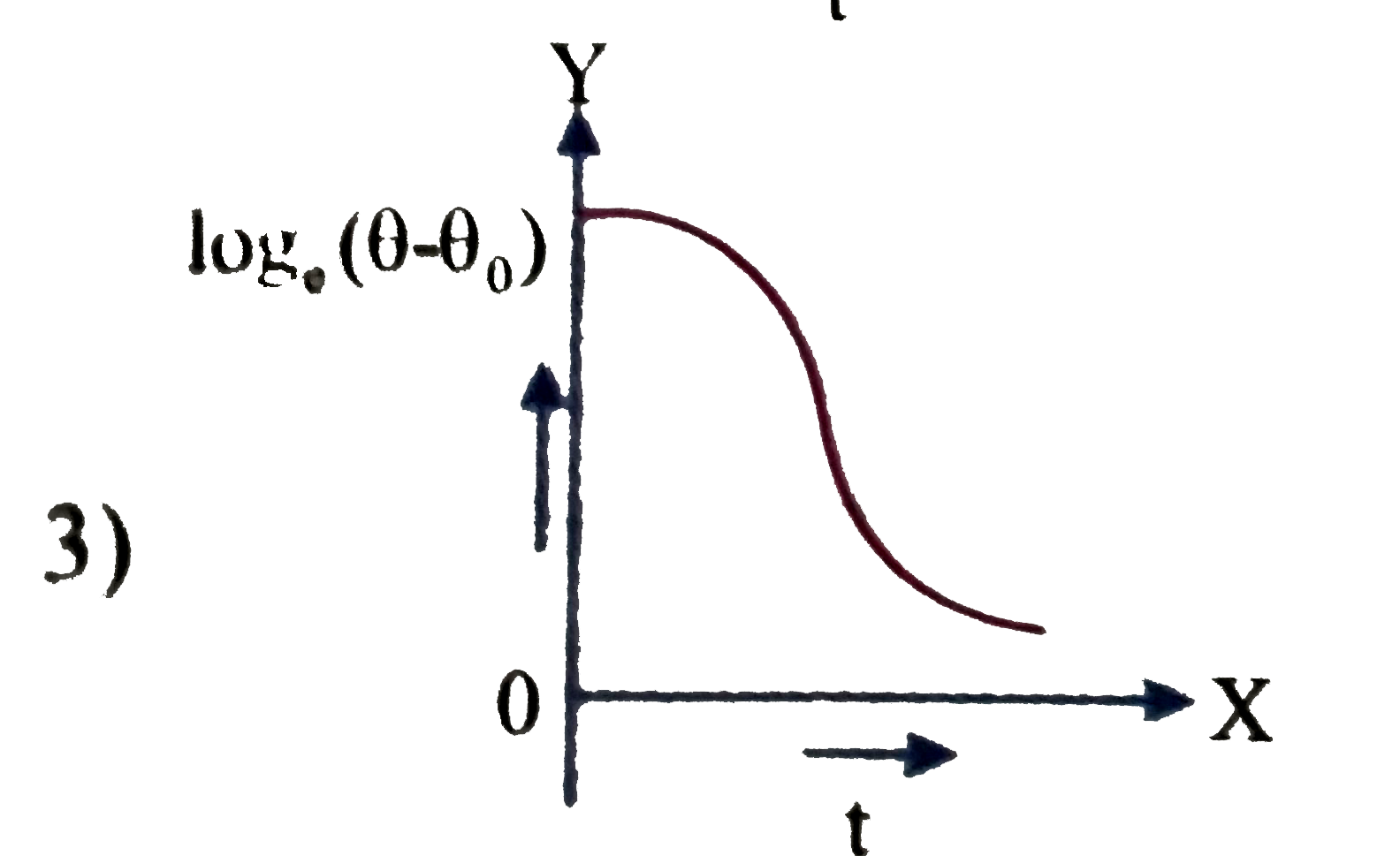
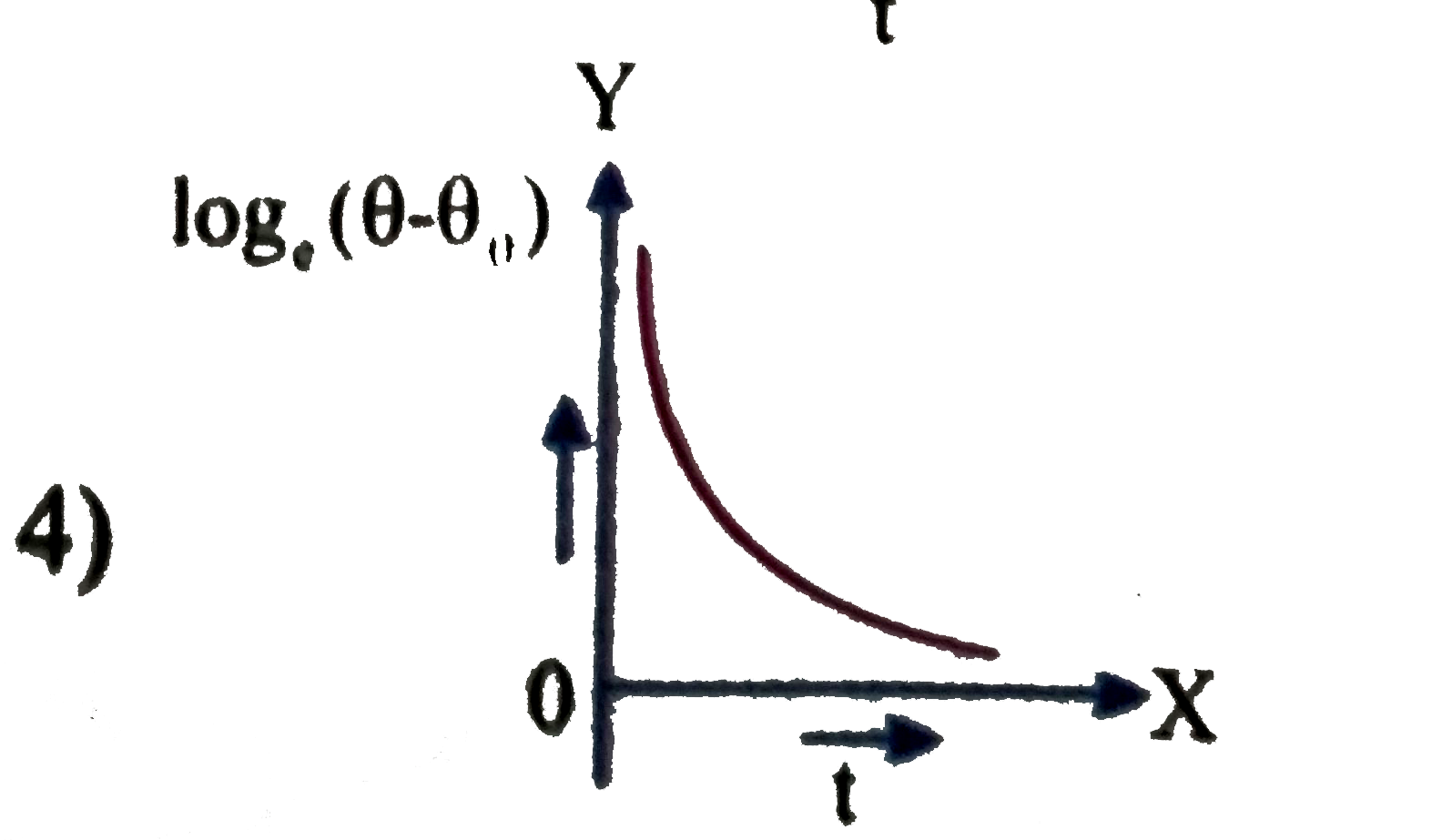
The correct Answer is:A
In so graph is a straight line .
Topper's Solved these Questions
- TRANSMISSION OF HEATBook:NARAYNAChapter:TRANSMISSION OF HEATExercise:NCERT BASED QUESTIONS
Explore 5 Videos
- TRANSMISSION OF HEATBook:NARAYNAChapter:TRANSMISSION OF HEATExercise:SINGLE ANSWER QUESTIONS Passage
Explore 1 Video
- TRANSMISSION OF HEATBook:NARAYNAChapter:TRANSMISSION OF HEATExercise:LEVEL-III (C.W)
Explore 1 Video
- THERMODYNAMICSBook:NARAYNAChapter:THERMODYNAMICSExercise:Exercise
Explore 187 Videos
- UNITS AND MEASUREMENTSBook:NARAYNAChapter:UNITS AND MEASUREMENTSExercise:STATEMENT TYPE QUESTION
Explore 23 Videos
Similar Questions
Knowledge Check
According to Newton’s law of cooling. The rate of loss of heat, −dθ/dtof the body is
Adirectly proportional to the sum of temperature of the body and Its surroundingsBInversely proportional to the sum of temperature of the body and Its surroundingsCdirectly proportional to the difference of temperature of the body and the surroundingsDInversely proportional to the sum of temperature of the body and the surroundingsThe correct curve between logeR and loge(θ−θo) is -
A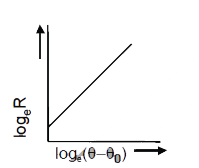 B
B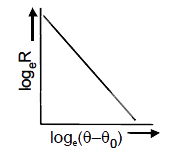 C
C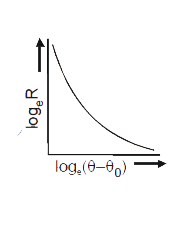 D
D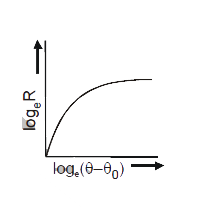
If the temperature of the body θ and time of cooling 't' and room temperature of the surrounding θ0. The cooling curve is
A B
B C
C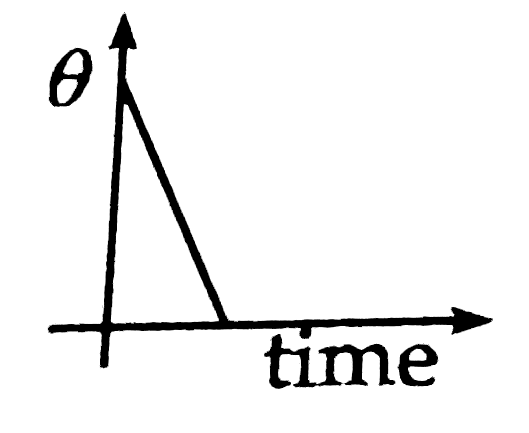 D
D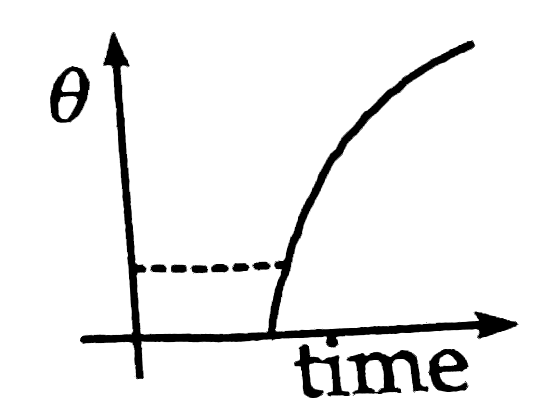
The correct graph between the temperature of a hot body kept in cooler surrounding and time is (Assume newton's law of cooling)
View SolutionThemperature of a body θ is slightly more than the temperature of the surrounding θ0 its rate of cooling (R) versus temperature of body (θ) is plotted its shape would be .
View SolutionFigure shows an electrical calorimeter to determine specific heat capacity of an unknown liquid, First of all, the mass of empty calorimeter (a copper container) is measured and suppose it is m1. Then the unknown liquid is poured in it. Now the combined mass of calorimeter+liquid system is measured and let it be m2. So the mass of liquid is (m2−m1). Initially both were at room temperature (θ0).
Now a heater is immeresed in if for time interval t. The voltage drop across the heater is V and current passing through it is I. Due to heat supplied, the temperature of both the liquid and calorimeter will rise simultaneously. After tsec, heater was switched off, and final temperature is θr. If there is no heat loss to surroundings. Heat supplied by the heater=Heat absorbed by the liquid+heat absorbed by the calorimeter (VI)t=(m2−m1)S1(θf−θ0)+m1Sc(θf−θ0)
The specific heat of the liquid S1=(VI)tθf−θ0−m1Sc(m2−m1)
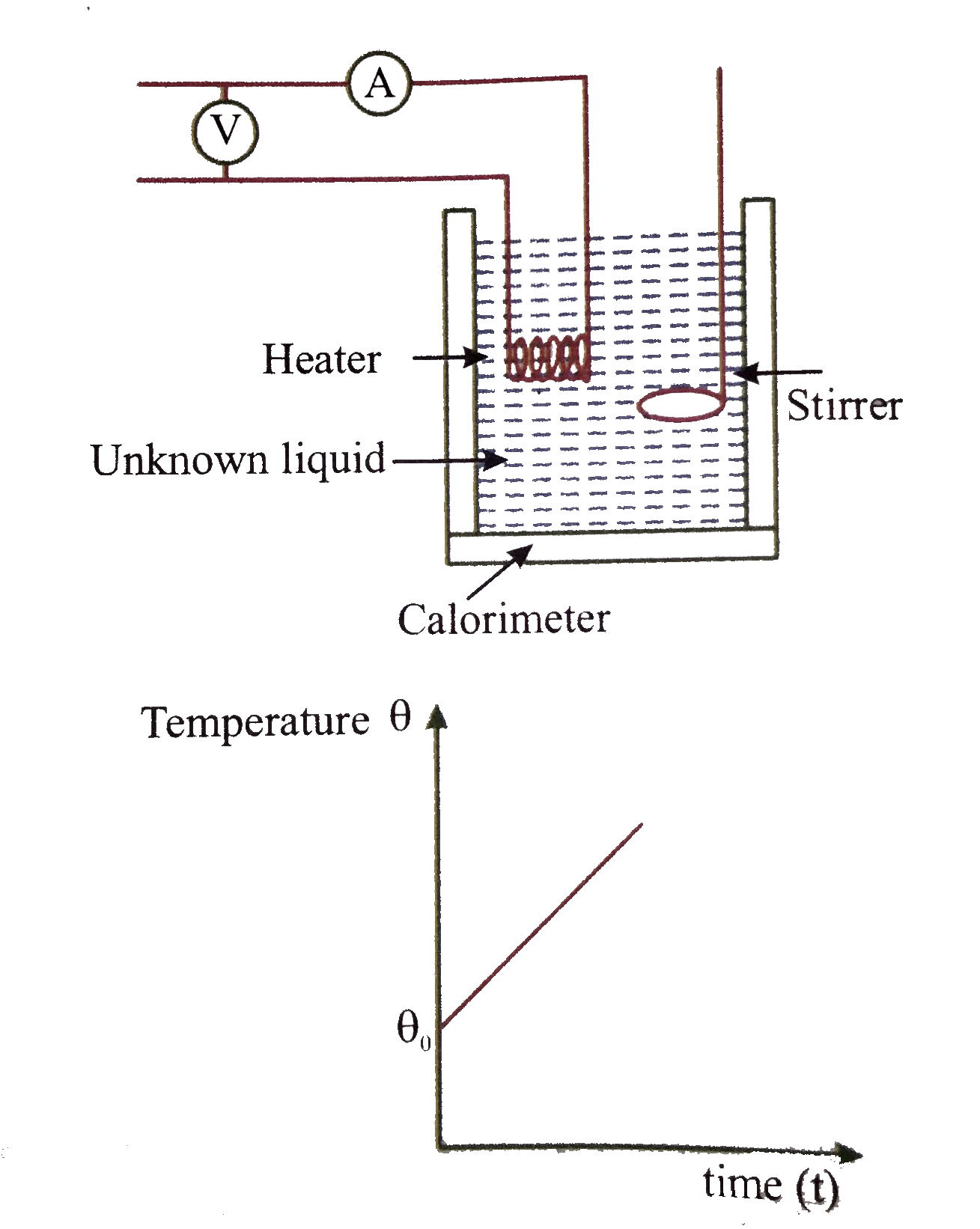
Radiation correction: There can be heat loss to environment. To compensate this loss, a correction is introduced.
Let the heater was on for tsec, and then it is switched off. Now the temperature of the mixture falls due to heat loss to environment. The temperature of the mixture is measured t/2sec. after switching off. Let the fall in temperature during this time is ɛ
Now the corrected final temperature is taken as θf=θf+ɛ
If the system were losing heat according to Newton's cooling law, the temperature of the mixture would change with time according to (while heater was on)
View SolutionA body at temperature θ0 having Newton's cooling constant K is placed in a surrounding having temperature T0 at time t = 0. The graph of temperature of the body as a function of time t is shown in the adjacent figure. A tangent on the curve is drawn at t = 0 as shown in the figure. Find the value of τ.

View SolutionA body cools in a surrounding which is at a constant temperature of θ0 Assume that it obeys Newton's law of cooling Its temperature θ is plotted against time t Tangents are drawn to the curve at the points P(θ=θ1) and Q(θ=θ2) These tangents meet the time axis at angle of ϕ2 andϕ1 as shown
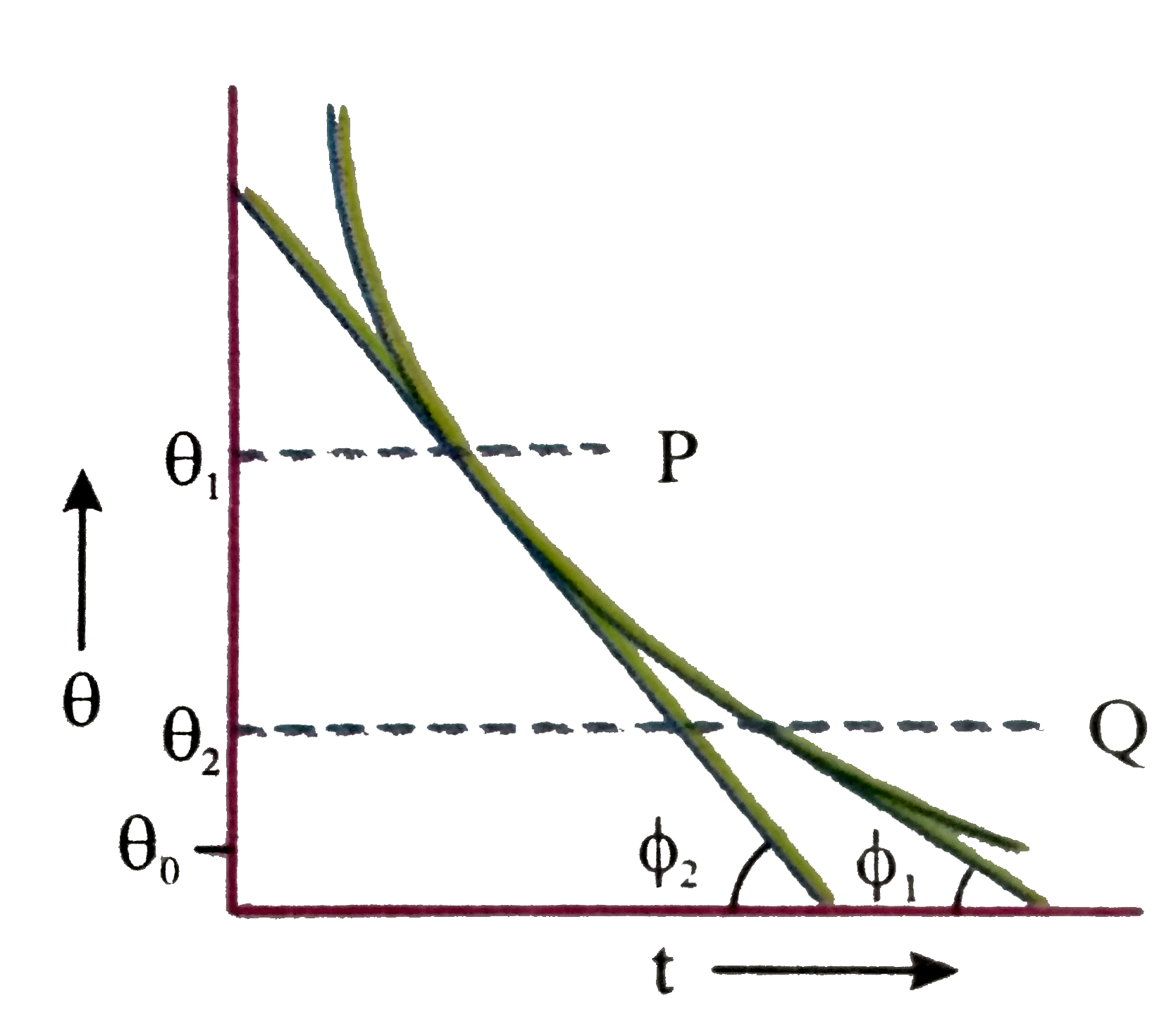 .
.
View Solution

