Find the current flowing through the resistance R1 of the circuit shown in Fig. If the resistances are equal to R1=10Ω.R2=20Ω and R3=30Ω, and the potential of points 1,2 and 3 are equal to φ1=10V,φ2=6V, and φ3=5V

Let us distribute the currents in the paths as shown in the figure. Now, φ1−φ2=iR1+i1R2 ....(1)
and φ1−φ3=iR1+(i−i1)R3 ....(2)
Simpliflying Eqs. (1) and (2) we get
i=R3(φ1−φ2)+R2(φ1−φ3)R1R2+R2R3+R3R1=0.2A

Topper's Solved these Questions
- ELECTRODYNAMICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:ELECTRODYNAMICSExercise:Constant Magnetic Fiels - Magnetics
Explore 69 Videos
- ELECTRODYNAMICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:ELECTRODYNAMICSExercise:Electromagnetic Induction
Explore 84 Videos
- ELECTRODYNAMICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:ELECTRODYNAMICSExercise:Electric Capacitance - Energy Of An Electric Field
Explore 46 Videos
- ELECTRICITY AND MAGNETISMBook:IE IRODOV, LA SENA & SS KROTOVChapter:ELECTRICITY AND MAGNETISMExercise:All Questions
Explore 6 Videos
- ELECTROMAGNETISMBook:IE IRODOV, LA SENA & SS KROTOVChapter:ELECTROMAGNETISMExercise:All Questions
Explore 24 Videos
Similar Questions
Find the current flowing through the resistance R1 of the circuit shown in figure if the resistances are equal to R1=10Ω,R2=20ΩandR3,=30Ω and the potentials of the points 1, 2, and 3 are equal to φ1=10V,φ2=6Vandφ3=5V
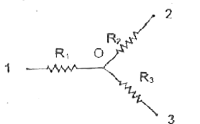
View SolutionFind the current flowing through the resistance R1 of the circuit shown in figure-3.103. the resistances are equal to R1=10Ω,R2=20Ω and R3=30Ω and the potentials of points 1,2 and 3 are given as V1=10V,V2=6V and V3=5V.
View Solution
Knowledge Check
In the given circuit, R1 = 10Ω R2=6Omega and E = 10V, then correct statement is
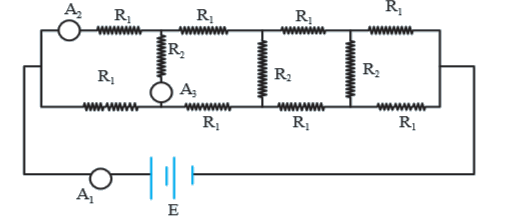 AEffective resistance of the circuit is 10ΩBR Reading of A1 is 1//2 amp.CReading of A2 is 1//2 ampDReading of A3 is 1//8 amp.
AEffective resistance of the circuit is 10ΩBR Reading of A1 is 1//2 amp.CReading of A2 is 1//2 ampDReading of A3 is 1//8 amp.In the circuit shown below E1=4.0V,R1=2Ω,E2=6.0V,R2=4Ω and R3=2Ω. The current I1 is
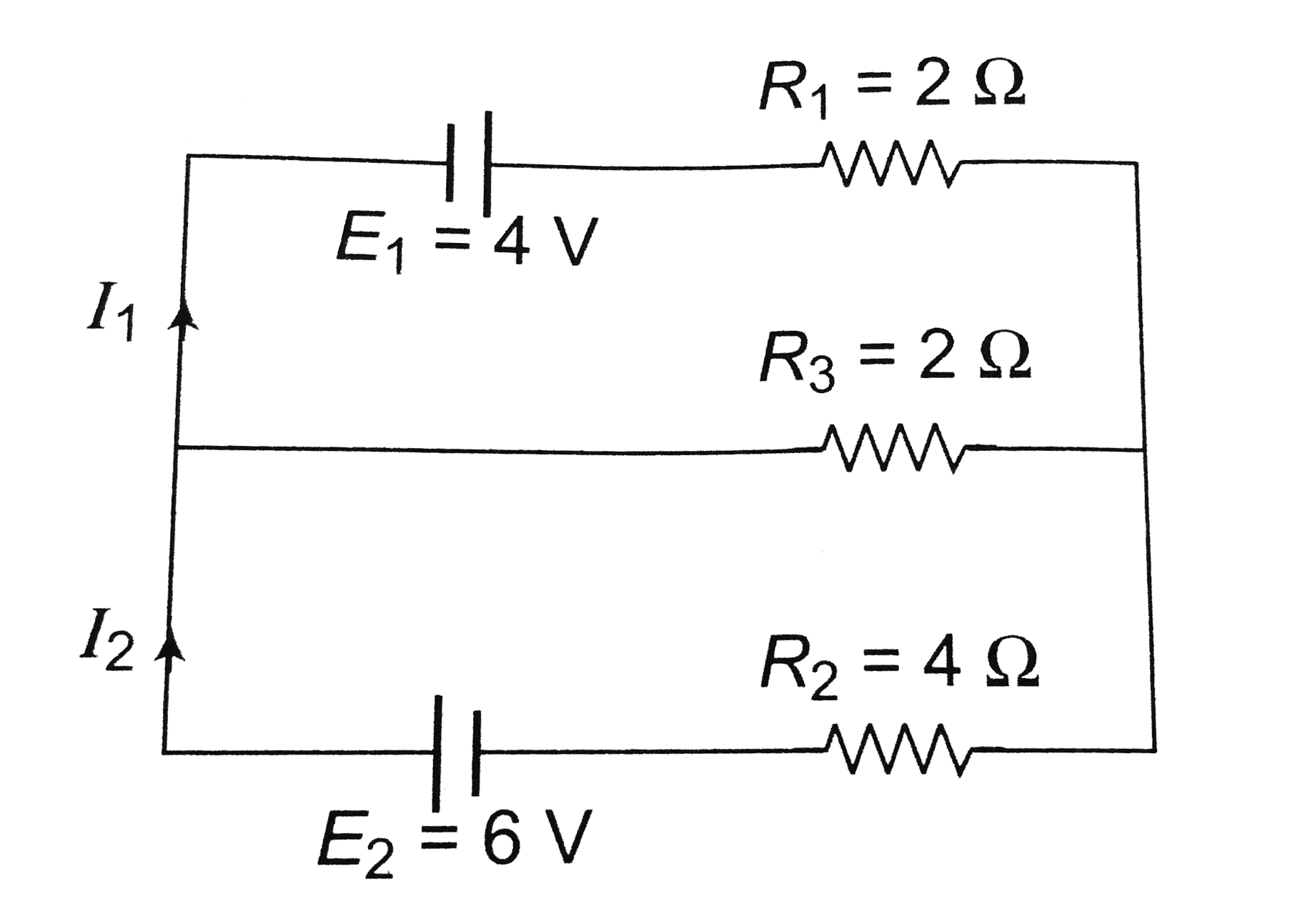 A1.6AB1.8AC1.25AD1.0A
A1.6AB1.8AC1.25AD1.0AThe potential difference in volt across the resistance R3 in the circuit shown in figure, is (R1=15Ω,R2=15Ω,R3=30Ω,R4=35Ω)
 A5B7.5C15D12.5
A5B7.5C15D12.5
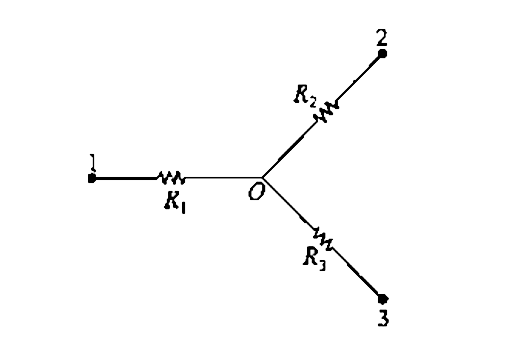
Find the currents in the Y connection of 3 resistances R1=10Ω, R2=20Ω and R3=30Ω. When the terminals of R1 , R3 and R3 are maintained at potentials V1 = 10V, V2=6V and V3 = 15V.
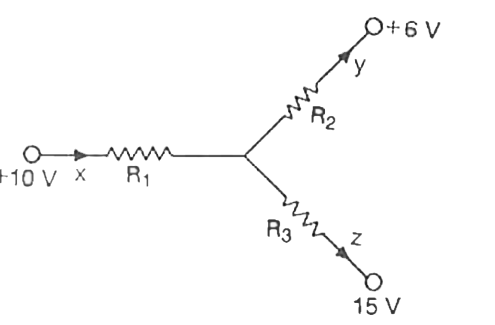
View SolutionFind the magnitude and direction of the current flowing through the resistance R in the circuit shown in Fig. if the emf's of the sources are equal to E1=1.5V and E2=3.7V and the resistances are equal to R1=10Ω,R2=20Ω,R=5.0Ω. The internal resistances of the sources are neglible.
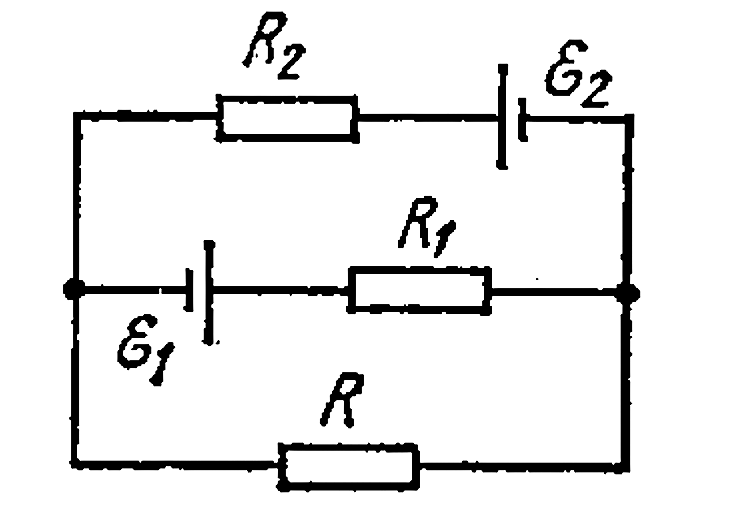
View SolutionDetermine the voltage drop across the resistance R1 in the circuit given in Fig. 4.55 with ε=90V,R1=5kΩ,R2=5kΩ,R3=10kΩ and R4=10kΩ.
View SolutionFind the current through the resistance R in Fig if R=10Ω and R=20Ω.

View SolutionFind a potential difference φA−φB between the plates of a capacitor C in the circuit shown in Fig, if the sources have emf'sE1=40V,E2=1.0V and the resistances are equal to R1=10Ω,R2=20Ω, and R3=30Ω. The internal resistances of the sources are negligble.
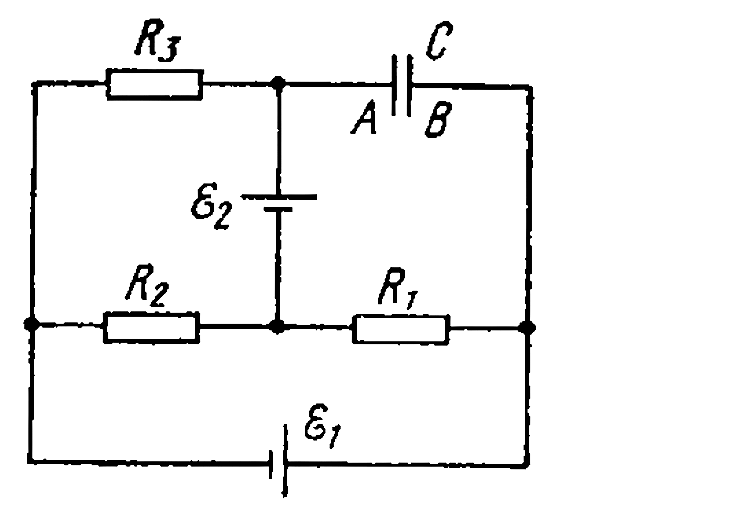
View Solution

