Two sources of equal emf are connected to an external resistance R. The internal resistance of the two sources areR1andR2(R1>R1). If the potential difference across the source having internal resistance R2 is zero, then
Let, us consider the current i, flowing through the circuit, as shown in the figure. Appling loop rule for the circuit, Δφ=0
2ξ+iR1+iR2+iR=0
or, i(R1+R2+R)=2ξ
or, i=2ξR+R1+R2
Now, if φ1−varπ2=0
ξ+iR1=0
or. 2ξR1R+R1+R2=ξ and 2R1=R2+R+R1
Thus, φ2−φ3=−ξ+iR2=0
or, 2ξR2R+R1+R2=ξ
So, R=R2−R1, which is the required resistance.

Topper's Solved these Questions
- ELECTRODYNAMICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRODYNAMICSEXERCISE - Constant Magnetic Fiels - Magnetics
69 Videos
- ELECTRODYNAMICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRODYNAMICSEXERCISE - Electromagnetic Induction
84 Videos
- ELECTRODYNAMICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRODYNAMICSEXERCISE - Electric Capacitance - Energy Of An Electric Field
46 Videos
- ELECTRICITY AND MAGNETISMBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRICITY AND MAGNETISMEXERCISE - All Questions
6 Videos
- ELECTROMAGNETISMBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTROMAGNETISMEXERCISE - All Questions
24 Videos
Similar Questions
Two cells of same emf ε, but different internal resistances r1 and r2 are connected to an external resistance R, as shown. The voltmeter V reads zero. Find R in terms of r1 and r2, and the voltage across the cell of internal resistance r2.
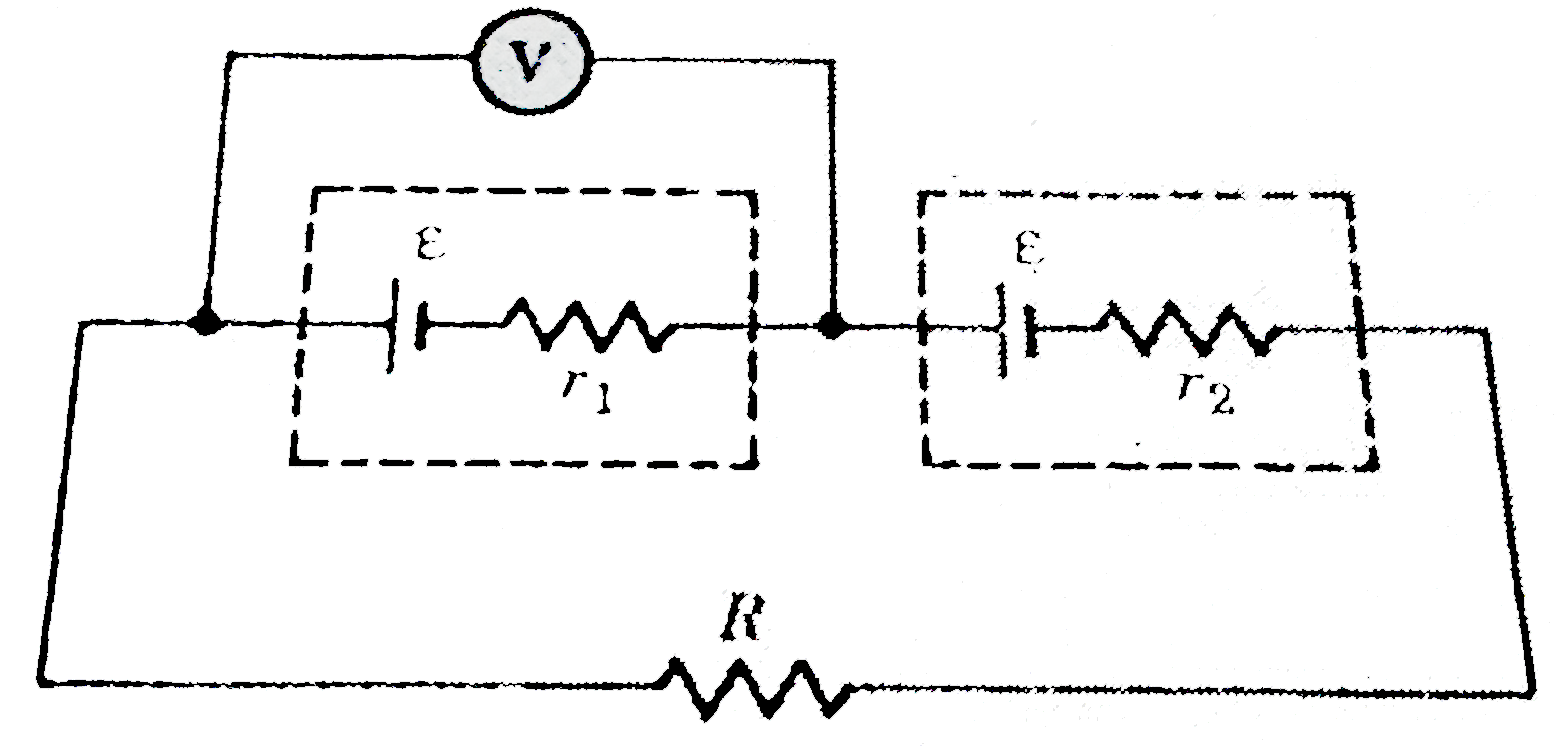
View SolutionTwo sources of current of equal emf are connected in series and having different internal resistance r1 and r2(r2>r1). Find the external resistance R at which the potential difference across the terminals of one of the sources becomes equal to zero.
View Solution
Knowledge Check
Two sources of equal emf are connected to an external resistance R. The internal resistance of the two sources are R1andR2(R1>R1). if the potential difference across the source having internal resistance R2 is zero, then
AR=R2−R1BR=R2×(R1+R2)/(R2−R1)CR=R1R2/(R2−R1)DR=R1R2/(R1−R2)Two cells, having the same emf, are connected in series through an external resistance R. Cells have internal resistance r1 and r2(r1>r2) respectively. When the circuit is closed, the potentail difference across the first cell is zero the value of R is
AR1−R2BR1+R22CR1−R22DR1+R2Two cells, having the same emf, are connected in series through an external resistance R. Cells have internal resistance r1 and r2(r1>r2) respectively. When the circuit is closed, the potentail difference across the first cell is zero the value of R is
Ar1+r2Br1−r2Cr1+r22Dr1−r22
Two cells, having the same emf, are connected in series through an external resistance R. Cells have internal resistance r1 and r2(r1>r2) respectively. When the circuit is closed, the potentail difference across the first cell is zero the value of R is
View SolutionTwo cells, having the same emf, are connected in series through an external resistance R. Cells have internal resistance r1 and r2(r1>r2) respectively. When the circuit is closed, the potential difference across the first cell is zero.
View SolutionTwo cells, having the same emf, are connected in series through an external resistance R. Cells have internal resistance r1 and r2(r1>r2) respectively. When the circuit is closed, the potential difference across the first cell is zero.
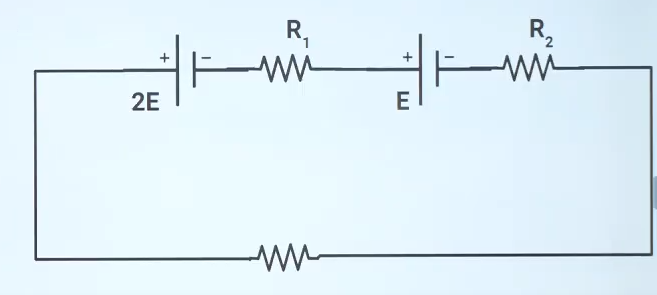
View SolutionInternal resistance of battery of emf 2E is R1 and battery of emf E is R2. If the potential difference across the cell of emf 2E is zero, then value of R is
View SolutionIf E is the emf of a cell of internal resistance r and external resistance R, then potential difference across R is given as
View Solution
