The cross-sectional radius of a pipeline decreases graudally as r=r0e−αx, where α=0.50ms−1, x is the distance from the pipeline inlet. Find the ratio of Reynolds numbers of two cross-sections separated by Δx=3.2m.
We know that, Reynold's number (Re) is defined as, Re=ρvl/η, where v is the velocity l is the characteristic length and η the coefficient of velocity. In the case of circular cross section the characteristic length is the diameter of cross-section d, and v is taken as average velocity of flow of liquid.
Now, Re1 (Reynold's number at x1 from the pipe end) =ρd1v1mη where v1 is the velocity at distance x1
and similarly, Re2=ρd2v2η so Re1Re2=d1v1d2v2
From equation of continuity, A1v1=A2v2
or, πr21v1=πr22v2 or d1v1r1=d2v2r2
d1v1d2v2=r2r1=r0e−αx2r0e−αx1=e−αΔx (as x2−x1=Δx)
Thus Re2Re1=eαΔx=5
Topper's Solved these Questions
- PHYSICAL FUNDAMENTALS OF MECHANICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:PHYSICAL FUNDAMENTALS OF MECHANICSExercise:Relativistic Mechanics
Explore 49 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:PHYSICAL FUNDAMENTALS OF MECHANICSExercise:Elastic Deformation Of Asolid Body
Explore 25 Videos
- OSCILLATIONS AND WAVESBook:IE IRODOV, LA SENA & SS KROTOVChapter:OSCILLATIONS AND WAVESExercise:Electromagnetic Waves, Radiation
Explore 36 Videos
- THERMODYNAMICS AND MOLECULAR PHYSICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:THERMODYNAMICS AND MOLECULAR PHYSICSExercise:Transport Phenomena
Explore 38 Videos
Similar Questions
A space is filled up with a charge with volume desnsity ρ=ρ0e−αr3, where ρ0 and α are positive constansts, r is the distance from the centre of this system. Find the magnitude of the electric field strength vector as a function of r. Investigate the obtained expresssion for the small and large values of r,i.e., at αr3<<1 and αr3>>1.
View SolutionAn infinitely long wire of uniform cross section carries a current whose current density varies as j=brα. Where b=107πunit,α=.1unit and r the distance from axis. The magnetic induction at a distance 0.25 from axis is given by n×53x10−2 tesla. Find n
View Solution
Knowledge Check
The area of cross-section of rod is given by A=A0(1+αx) where A0 & α are constant and x is the distance from one end. If the thermal conductivity of the material is K. What is the thermal resistancy of the rod if its length is l0?
AKA0αln(1+αl0)B1KA0αln(1+αl0)CαKA0αln(1+αl0)DKA0αln(1+αl0)The electric components in the figure are Ex=αx1/2,Ey=0,Ez=0 where α=800N/m2 if a=0.1m is the side of cube then the charge with in the cube is
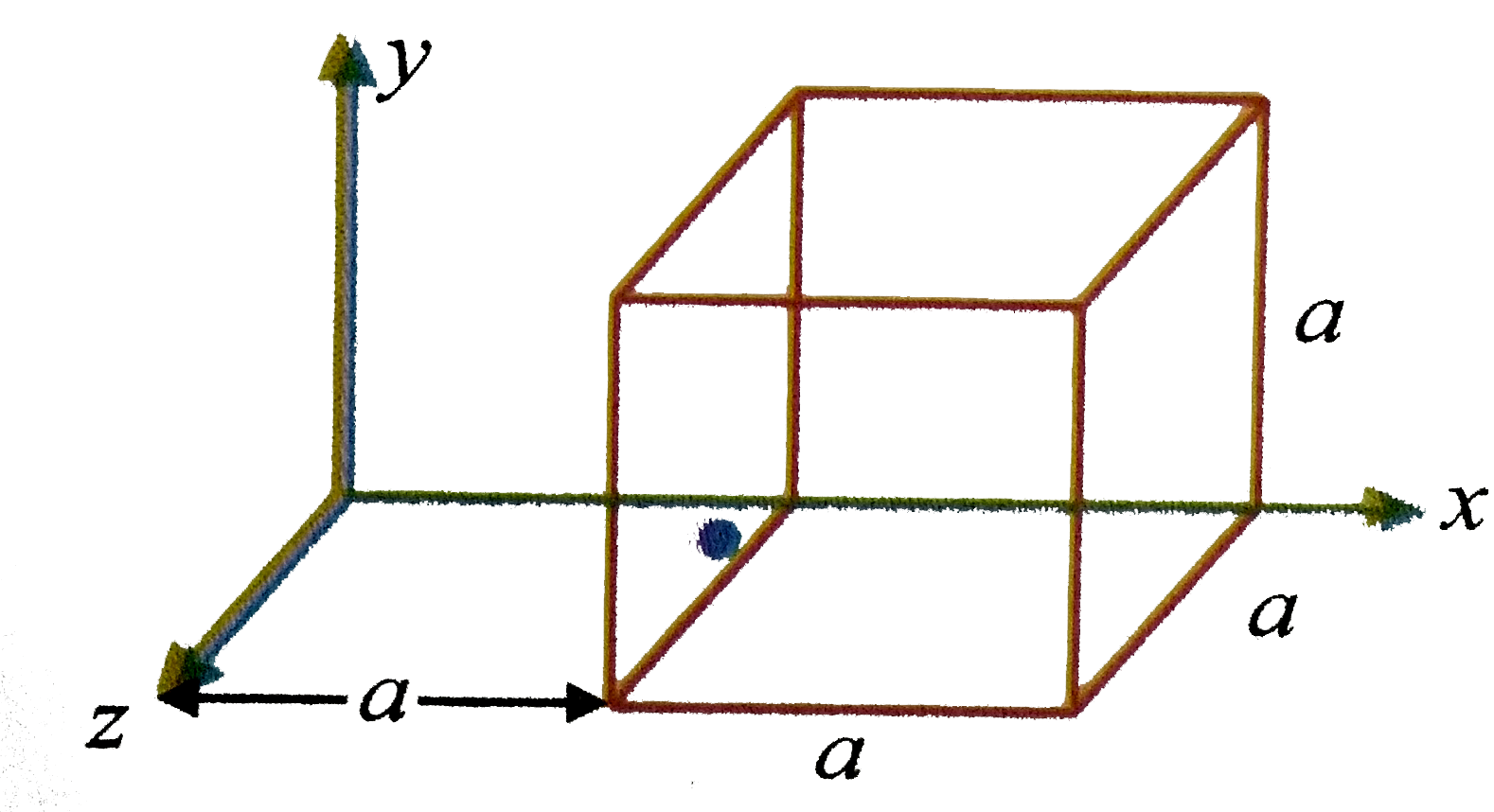 A9.27×10−12CB6×10−12CC2.5×10−12CDZero
A9.27×10−12CB6×10−12CC2.5×10−12CDZeroA solid cylindrical wire of length l has cross-section radius a as shown below. The specific resistance of material is given as ρ=ρ0r, where r is distance from axis of cylinder and ρ0 is a positive constant quantity. The resistance across its ends is :
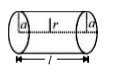 Aρ0l2πaBρ0lπa2Cρ0lπaD2ρ0lπ
Aρ0l2πaBρ0lπa2Cρ0lπaD2ρ0lπ
A long cylinder of uniform cross section and radius R is carrying a current i along its length and current density is uniform cross section and radius r in the cylinder parallel to its length. The axis of the cylinderical cavity is separated by a distance d from the axis of the cylinder. Find the magnetic field at the axis of cylinder.
View SolutionThe current through a wire depends on time as
I=i0+αt,
where i0=10Aandα=4As−1.Find the charge crossed through a section of the wire in 10 second
View SolutionThere is one rod of length L. the resistivity of its material is given by ρ=αx+β. Here x is the distance of α point on rod from one of its ends. Assume A as the area of cross section of rod. Find the electrical resistance of the rod.
View SolutionA current is flowing through a cylinderical conductor of radius R, such that current density at any cross-section is given by J=J0(1−rR), where r is radial distance from axis of the cylinder .Calculate the total current through the cross-section of the conductor.
View SolutionResistivity of the material of a conductor of uniform cross-section varies along its length as ρ=ρ0(1+αx). Find its resistance if its length is L and area of cross-section is A.
View Solution

