_E01_234_Q01.png)
A thin horizontal disc of radius R=10cm is located with in a cylindrical cavity filled with oil whose viscosity η=0.08P (figure) The distance between the disc and the horizontal planes of the cavity is equal to h=1.0 mm find the power developed by the viscous forces acting ont he disc when it rotates with the angular velocity ω=60rad/s. The end effect are to be neglected.
When the disc rotates the fluid in contact, with, carotates but the fluid in contact with the walls of the cavity does not rotate. A velocity gradient is then set up leading to viscous forces. At a distance r from the axis the linear velocity is ωr so there is a velocity gradient ωrh both in the upper and lower clearance. The corresponding force on the element whose radiul width is dr is
η2πdrωrh (from the formula F=ηAdvdx)
The torque due to this force is
η2πrdrωrhr
and the net torque considering both the upper and lower clearance is
2R∫0η2πr3drωh
=πR4ωη/h
So power developed is
P=πR4ω2η/h=9⋅05W (on putting the values).
(As instructed end effects i.e. rotation of fluid in the clearance r>R has been neglected.)
Topper's Solved these Questions
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Relativistic Mechanics49videos
PHYSICAL FUNDAMENTALS OF MECHANICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Elastic Deformation Of Asolid Body25videos
PHYSICAL FUNDAMENTALS OF MECHANICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Electromagnetic Waves, Radiation36videos
OSCILLATIONS AND WAVES
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - THERMODYNAMICS AND MOLECULAR PHYSICSEXERCISE - Transport Phenomena38videos
THERMODYNAMICS AND MOLECULAR PHYSICS
Similar Questions
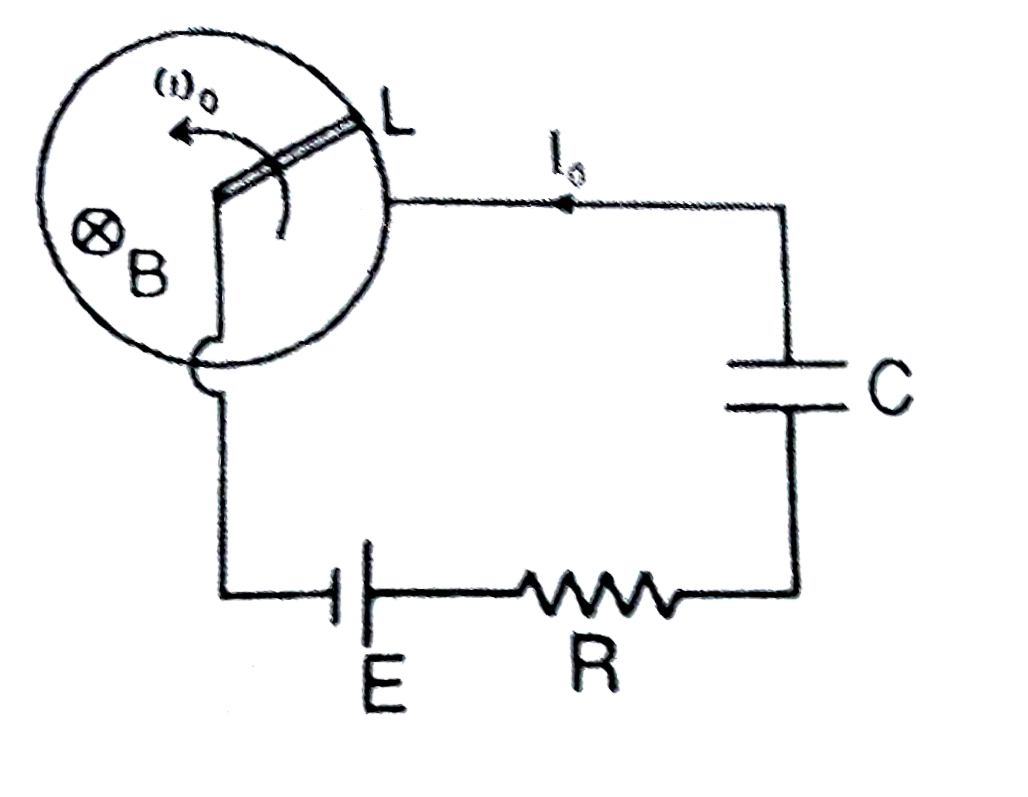
L is a smooth conducting loop of radius l=1.0 m & fixed in a horizontal plane. A conducting rod of mass m=1.0 kg and length slightly greater than l hinged at the centre of the loop can rotate in the horizontal plane such that the free end slide on the rim of the loop. There is a uniform magnetic field of strength B=1.0 T directed vertically downward. The rod is rotated with angular velocity ω0=1.0rad/s and left. The fixed end of the rod and the rim of the loop are connected through a battery of emf . E, a resistor of resistance R=1.0Ω, and intially uncharged capacitor of capacitance C=1.0 F in series. Find :
(i) the time dependence of emf . E such that the current I0=1.0A in the circuit is constant.
(ii) energy supplied by the battery by the time rod stops.
View SolutionThe small particle of mass m is given an initial high velocity in the horizontal plane and winds its cord around the fixed vertical shaft of radius 1m. All motion occurs essentially in the horizontal plane. If the angular velocity of the cord is 0.8 rad/s when the distance from the particle to the tangency point is 5m, determine the angular velocity ω (in rad//s) of the cord after it has turned through an angle 1 rad.
View Solution
Knowledge Check
- Question 1 - Select One
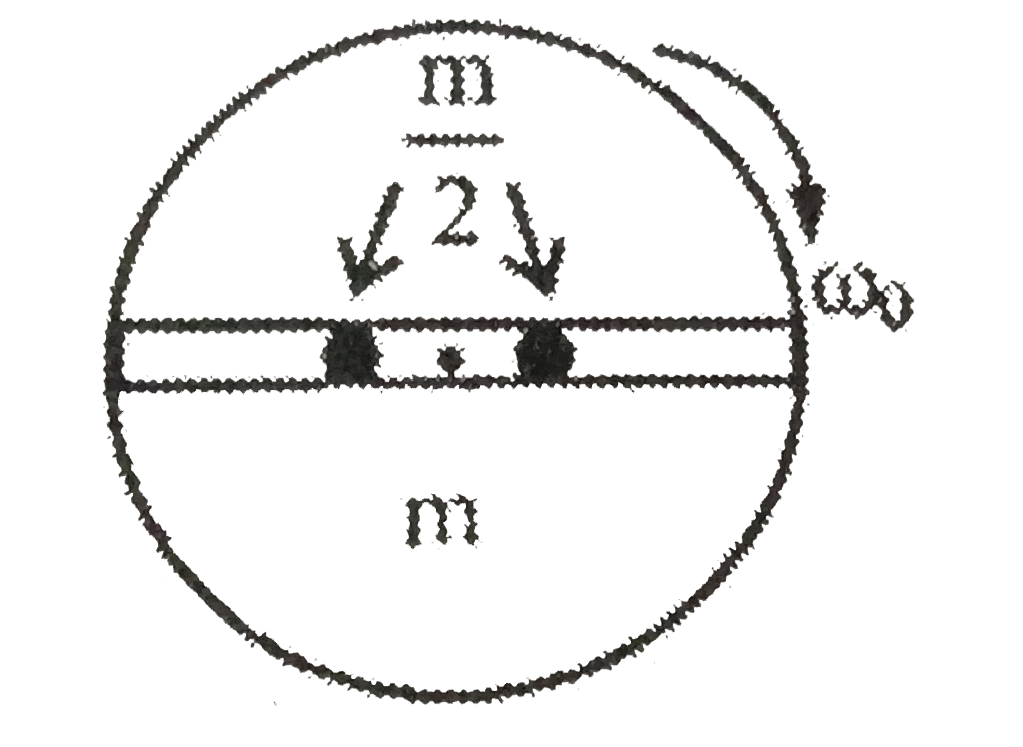
A disc of mass m and radius R is free to rotate in a horizontal plane about a vertical smooth fixed axis passing through its centre. There is a smooth groove along the diameter of the disc and two small balls of mass m/2 each are placed in it on either side of the centre of the disc as shown in Fig. The disc is given an initial angular velocity ω0 and released.
The angular speed of the disc when the balls reach the end of the disc isAω02Bω03C2ω03Dω04 - Question 2 - Select One
A disc of mass m and radius R is free to rotate in a horizontal plane about a vertical smooth fixed axis passing through its centre. There is a smooth groove along the diameter of the disc and two small balls of mass m/2 each are placed in it on either side of the centre of the disc as shown in Fig. The disc is given an initial angular velocity ω0 and released.
The net work done by forces exerted by the disc on the ball for the duration ball remains on the disc isA2mR2ω209BmR2ω2018CmR2ω206DmR2ω209 - Question 3 - Select One
A disc of mass 'm' and radius R is free to rotate in horizontal plane about a vetical smooth fixed axis passing through is centre. There is a smooth groove along the diameter of the disc and two small balls of mass m/2 each are placed in it on either side of the centre of the disc as shown in fig. The disc is given initial angular velocity ω0 and released. The angular speed of the disc when the balls reach the end of the disc is -
Aω02Bω03C2ω03Dω04
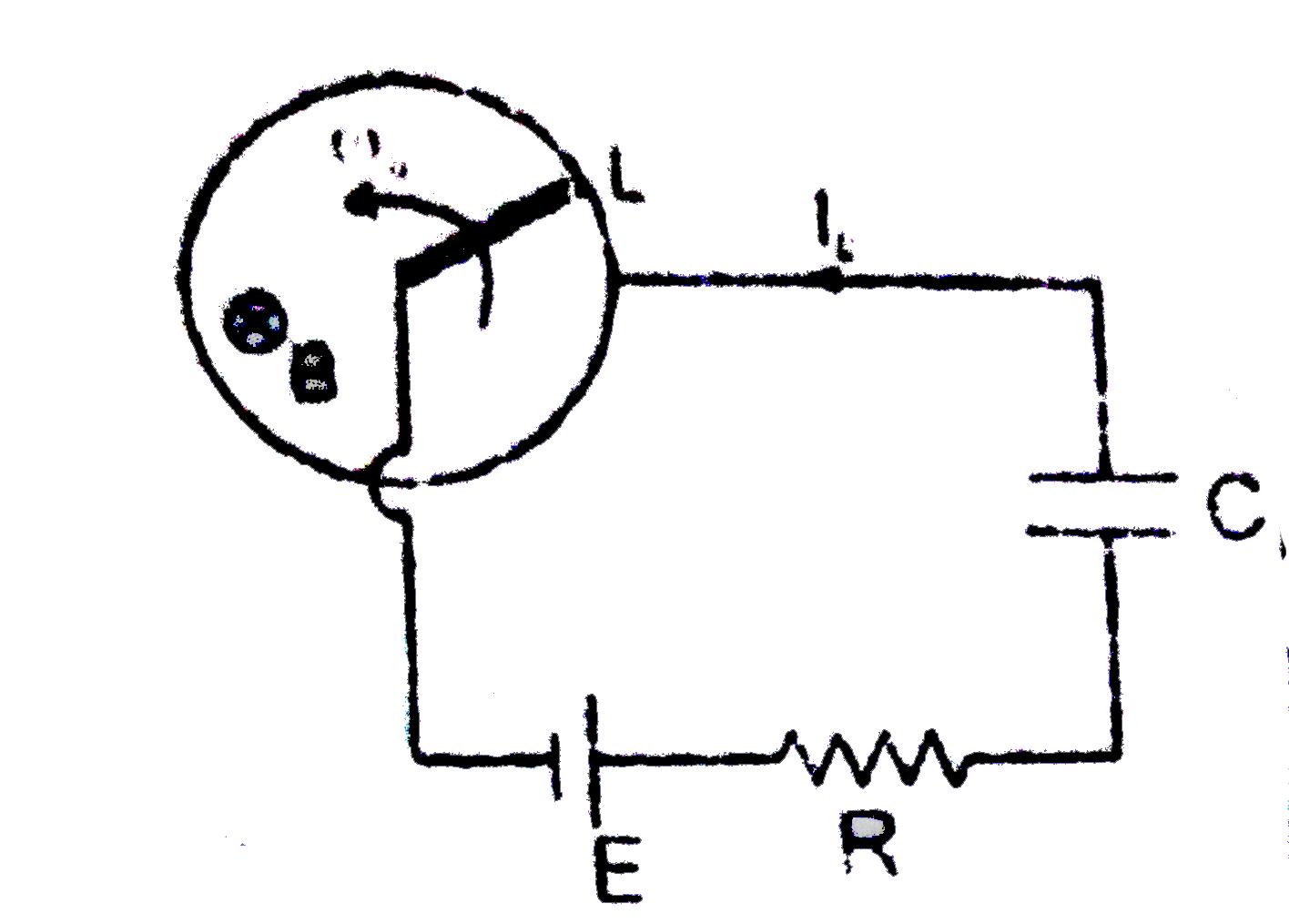
L is a smooth conducting loop of radius l=1.0m & fixed in a horizontal plane.A conducting rod of mass m=1.0kg and length slightly greater than l higed at the centre of the loop can rotate in the horizontal plane such that the free end slides on the rim of the loop.There is a uniform magnetic field of strength B=1.0T directed vertically downward.The rod is rotated with angular velocity ω0=1.0rad/s and left.The fixed end of the rod and the rim of the loop are connected through a battery of e.m.f E a resistance R=1Ω, and initially uncharged capacitor of capacitance C=1.0F in series.Find
(i)the time dependence of e.m.f M such that the current I0=1.0A in the circuit is contant.
(ii)energy supplied by the battery by the time rod stops.
View SolutionA horizontally oriented uniform disc of mass M and radius R rotates freely about a stationary vertical axis passing through its centre. The disc has a radial guide along which can slide without friction a small body of mass m. A light thread running down through the hollow axle of the disc is tied to the body initially the body was located at the edge of the disc and the whole system rotated with ann angular velocity ω0. Then by means of a force F applied to the lower and of the thread the body was slowly pulled to the rotation axis. find:
(a). The angular velocity of the system in its final state.
(b). The work performed by the force F.View SolutionA disc shaped body (having a hole shown in the figure) of mass m=10kg and radius R=109m is performing pure rolling motion on a rough horizontal surface. In the figure point O is geometrical center of the disc and at this instant the centre of mass C of the disc is at same horizontal level with O. The radius of gyration of the disc about an axis pasing through C and perpendicular to the plane of the disc is R2 and at the insant shown the angular velocity of the disc is ω=√gR rad/sec in clockwise sence. g is gravitation acceleration =10m/s2. Find angular acceleation α ( in rad/s2) of the disc at this instant.
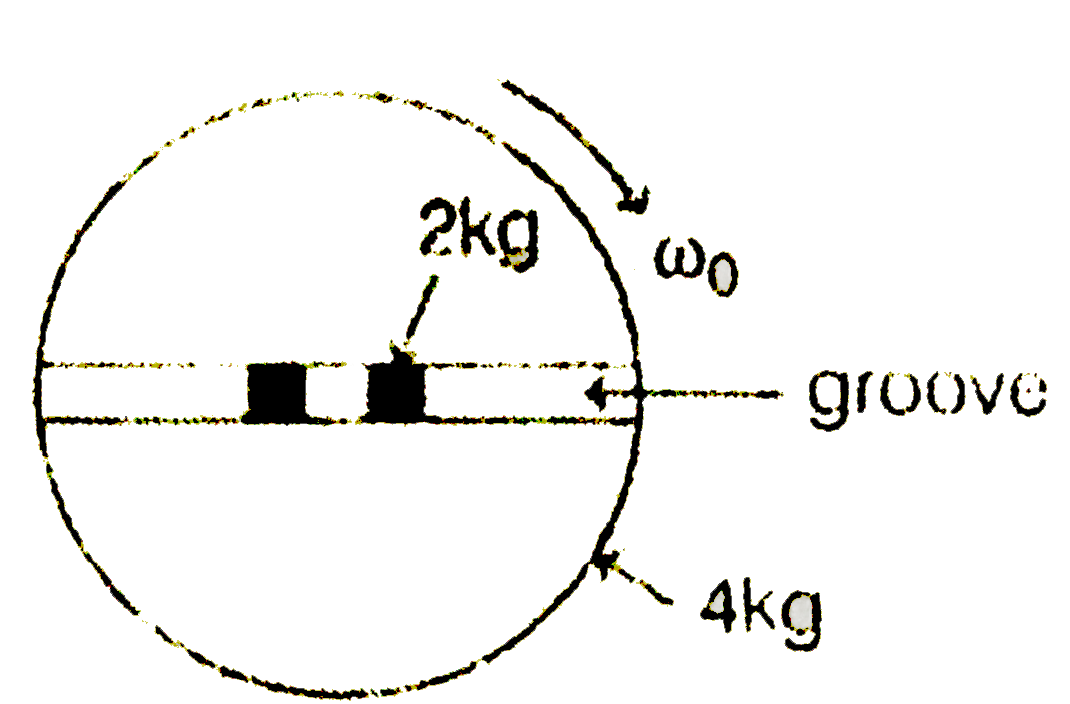
View SolutionA disc of mass 4 kg and radius 6 metre is free to rotate in horizontal plane about a vertical fixed axis passing through its centre. There is a smooth groove along the diameter of the disc and two small blocks of masses 2 kg each are placed in it on either side of the centre of the disc as shown in figure. The disc is given initial angular velocity ω0 =12 rad/sec and released. Find the angular speed of disc (in radian/sec) when the blocks reach the ends of the disc.
View SolutionA smooth disc of mass M and radius L√3 is placed at rest horizontally on a smooth horizontal surface. A massless pin is fixed at point P at a distance L/2 from centre O of the disc as shown in the figure. Now a thin uniform rod of mass M and length L is placed horizontally on the surface of the disc parallel to the line OP such that its mid point and centre O of the disc just coincide as shown in figure. Now rod has given angular velocity ω0=24rad/sec in counter clockwies direction as shown. As a result, the end of the rod strikes the pin P and stricks to it rigidly. Calculate the angular velocity of disc just after collision.
View Solution