Water flows out of a big tank along a tube bent at right angles, the inside radius of the tube is equal to r=0.50cm (figure). The length of the horizontal section of the tube is equal to l=22cm. The water flow rate is Q=0.50 litres per second. Find the moment of reaction forces of flowing water, acting on the tube's walls, relative to the point O.

Let the velocity of water flowing through the tube at a certain instant of time be u, then u=Qπr2, where Q is the rate of flow of water and πr2 is the cross section area of the tube.
From impulse momentum theorem, for the stream of water striking the tube corner, in x-direction in the time interval dt,
Fxdt=−ρQudt or Fx=−ρQu
and similarly, Fy=ρQu
Therefore, the force exerted on the water stream by the tube,
→F=−ρQu→i+ρQu→j
According to third law, the reaction force on the tube's wall by the stream equals (−→F)
=ρQu→i−ρQu→j.
Hence, the sought moment of force about 0 becomes
→N=l(−→i)×(ρQu→i−ρQu→j)=ρQul→k=ρQ2πr2l→k
and ∣∣→N∣∣=ρQ2lπr2=0⋅70N⋅m

Topper's Solved these Questions
- PHYSICAL FUNDAMENTALS OF MECHANICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:PHYSICAL FUNDAMENTALS OF MECHANICSExercise:Relativistic Mechanics
Explore 49 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:PHYSICAL FUNDAMENTALS OF MECHANICSExercise:Elastic Deformation Of Asolid Body
Explore 25 Videos
- OSCILLATIONS AND WAVESBook:IE IRODOV, LA SENA & SS KROTOVChapter:OSCILLATIONS AND WAVESExercise:Electromagnetic Waves, Radiation
Explore 36 Videos
- THERMODYNAMICS AND MOLECULAR PHYSICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:THERMODYNAMICS AND MOLECULAR PHYSICSExercise:Transport Phenomena
Explore 38 Videos
Similar Questions
Water flows out of a big tank along a tube bent at right angles, the inside of the tube is of radius r. The length of the horizontal portion is l. The rate of water flow is Q. Find the moment of reaction forces of flowing water, acting on the tube walls relative to point O.
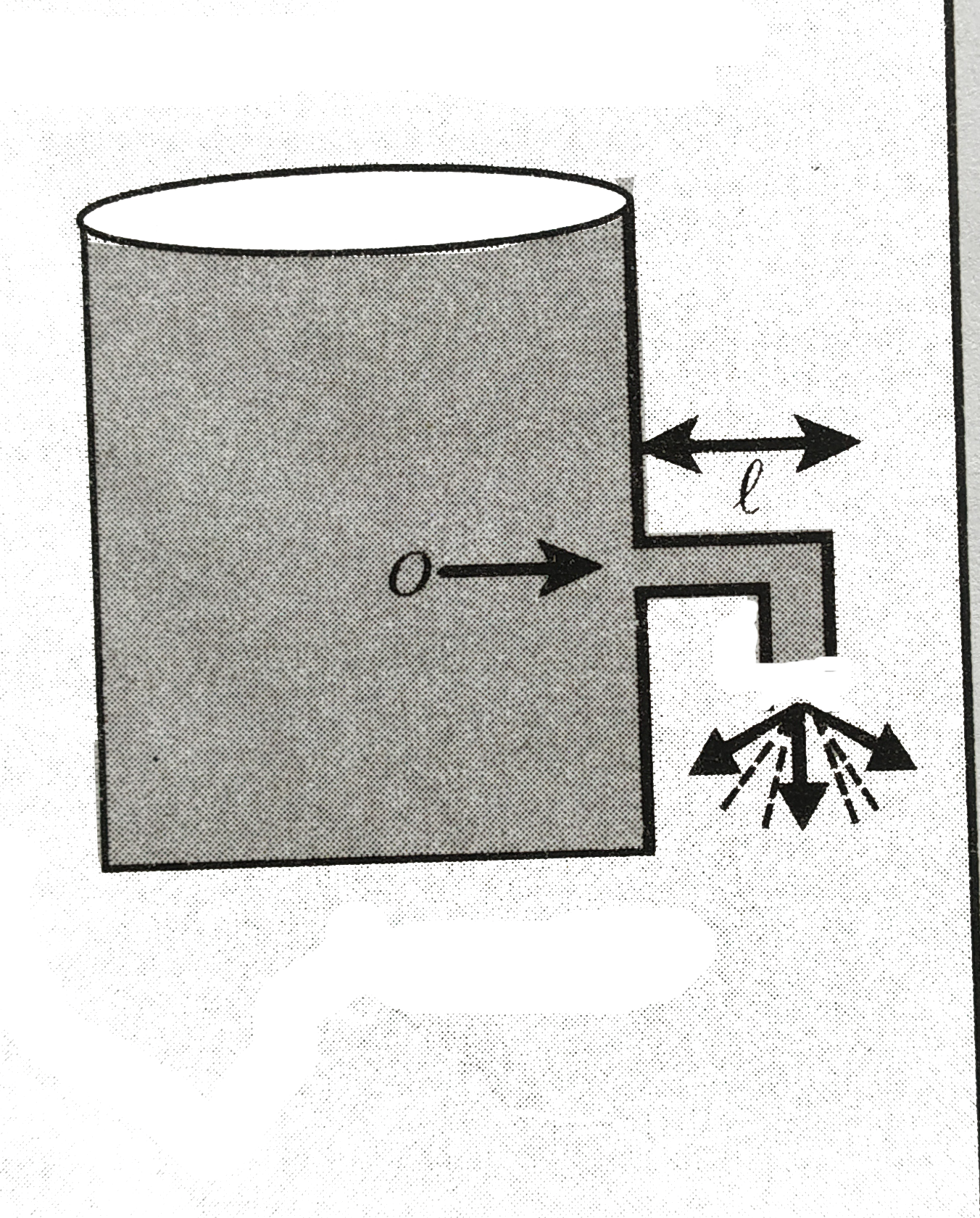
View SolutionWater flows out of a big tank along a horizontal tube of length l and radius r and bent at right angles at the other end. The rate of flow is Q. Calculate the moment of the force exerted by the water on the tube about the other end. Neglect viscosity of water.
View SolutionFrom a pipe of inner radius 0.75 cm, water flows at the rate of 7 m per second. Find the volume in litres of water delivered by the pipe in 1 hour.
View SolutionA bent tube is lowered into a water stream as shown in figure. The velocity of the stream relative to the tube is equal to v=2.5m/s. The closed upper end of the tube located at the height h0=12cm has a small orifice. To what height h will the water jet spurt?
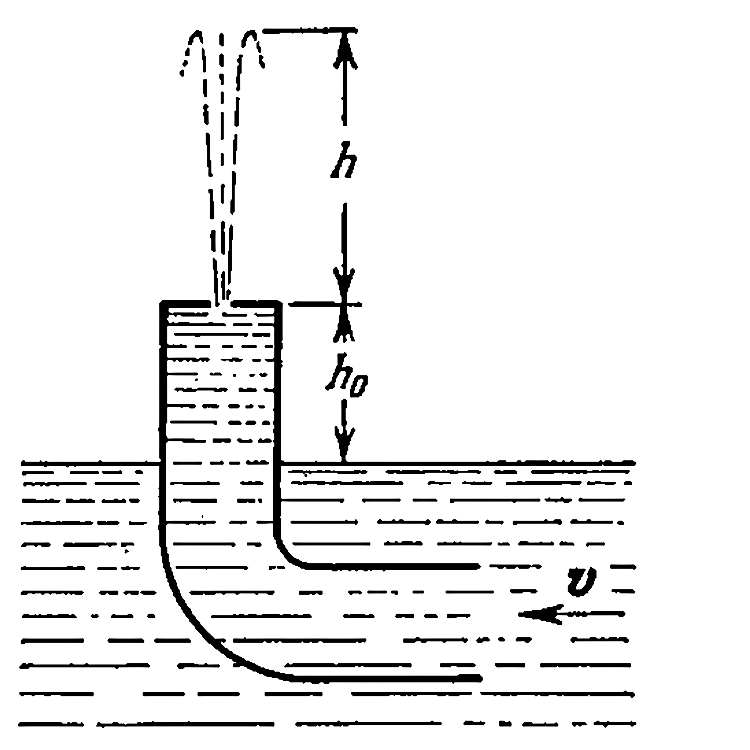
View SolutionWater flow through horizontal pipe of varying cross-section at the rate of 1/2 liter per second. Determine the velocity of flow of water at a point where the diameter is (a) 4cm (b) 2cm.
View SolutionA bent tube is lowered into water stream as shown in figure. The velocity of the stream relative to the tube is equal to v=2.5m/s. The closed upper end of the tube located at a height of 12cm has a small orifice. To what height h will the water jet spurt ?

View SolutionFrom a tap of inner radius 0.75cm, water flows at the rate of 7m per second. Find the volume in litres of water delivered by the pipe in one hour.
View SolutionWater is flowing through a horizontal tube of non-uniform cross-section. At a place, the radius of the tube is 1.0cm and the velocity of water is 2m/s. What will be the velocity of water where the radius of the pipe is 2.0cm?
View SolutionA bent tube is lowered into a water stream as shown in figure. The velocity of the stream relative to the tube is equal to v=2.5 m/s. The closed upper end of the tube located at the height h0=12cm has a small orifice. To what height h will the water jet spurt ?

View SolutionWater flows through the tube shown in figure. The areas of cross section of the wide and the narrow portions of the tube are 5cm2and2cm2 respectively. The rate of flow of water through the tube is 500cm3s−1 . Find the difference of mercury levels in the U-tube.

View Solution

