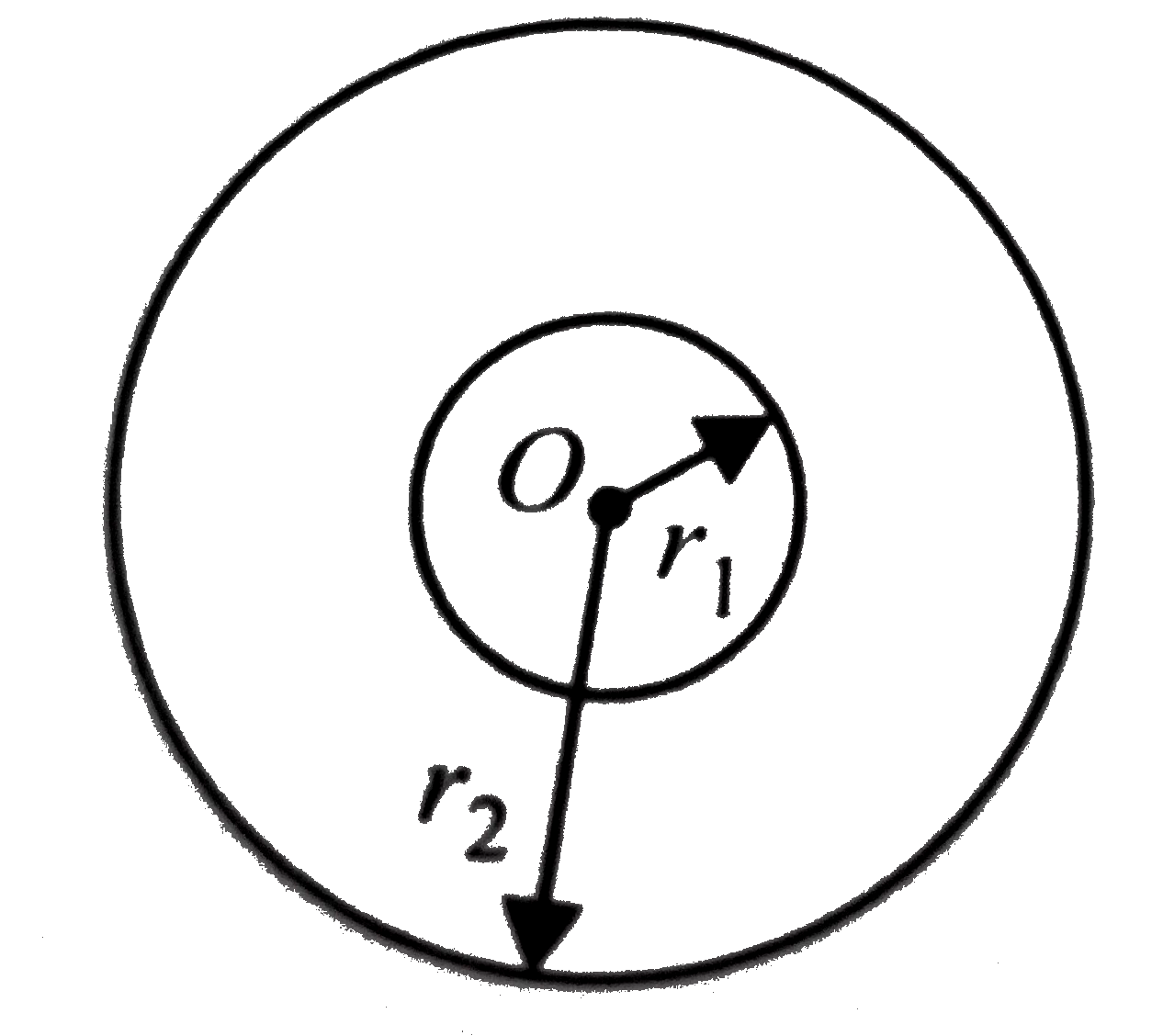
A fluid with viscosity η fills the space between two long co-axial cylinders of radii R1and R2, with R1<R2. The inner cylinder is stationary while the outer one is rotated with a constant angular velocity ω2. The fluid flow is laminar. Taking into account that the friction force acting on a unit area of a cylindrical surface of radius r is defined by the formula σ=ηr(∂ω/∂r), find:
(a) the angular velocity of the rotating fluid is as a function of radius r,
(b) the moment of the friction forces acting on a unit length of the outer cylinder.
(a) Let us consider an elemental cylinder of radius r and thickness dr then from Newton's formula
F=2πrlηrdωdr=2πlηr2dωdr
and moment of this force acting on the element,
N=2πr2lηdωdrr=2πr3lηdωdr
or, 2πlηdω=Ndrr3 (2)
As in the previous problem N is constant when conditions are steady
Integrating, 2πlηω∫0dω=Nr∫R1drr3
or, 2πlηω=N2[1R21−1r2] (3)
Putting r=R2,ω=ω2, we get
2πlηω2=N2[1R21−1R22] (4)
From (3) and (4),
ω=ω2R21R22R22−R21[1R21−1r2]
(b) From Eq. (4),
N1=Nl=4πηω2R21R22R22−R21

Topper's Solved these Questions
- PHYSICAL FUNDAMENTALS OF MECHANICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Relativistic Mechanics
49 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Elastic Deformation Of Asolid Body
25 Videos
- OSCILLATIONS AND WAVESBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Electromagnetic Waves, Radiation
36 Videos
- THERMODYNAMICS AND MOLECULAR PHYSICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - THERMODYNAMICS AND MOLECULAR PHYSICSEXERCISE - Transport Phenomena
38 Videos
Similar Questions
A gas fills up the space between two long coaxial cylinders of radii R1 and R2, with R1<R2. The outer cylinder rotates with a fairly low angular velocity ω about the stationary inner cylinder. The moment of friction forces acting on a unit length of the inner cylinder is equal to N1. Find the viscosity coefficient η of the gas taking into account that the friction force acting on a unit area of the cylindrical surface of radius r is determined by the formule σ=ηr(∂ω/∂r).
View SolutionFind the temperature distribution in the space between two coaxial cylinders of radii R1 and R2 filled with a uniform heat conducting substance if the temperatures of the cylinders are constant and are equal to T1 and T2 respectively.
View Solution
Knowledge Check

There are two concentric cylinders of radii R1 and R2 as shown. The narrow space between the two cylinders is filled with liquid of viscosity μ. The inner cylinder is held stationary by means of a torsional spring of stiffness G. the outer cylinder is rotated with constant angular speed ω. The torque acting on the inner cylinder due to shearing action of thhe liquid:AπμωR42h+2πμωHR21R2R2−R1BπμωHR21R2R2−R1CπμωHR21R2R2−R1+μωR43hDπμωR42hA cylindrical space of radius R is filled with a uniform magnetic induction parallel to the axis of the cylinder. If B charges at a constant rate, the graph showin the variation of induced electric field with distance r from the axis of cylinder is
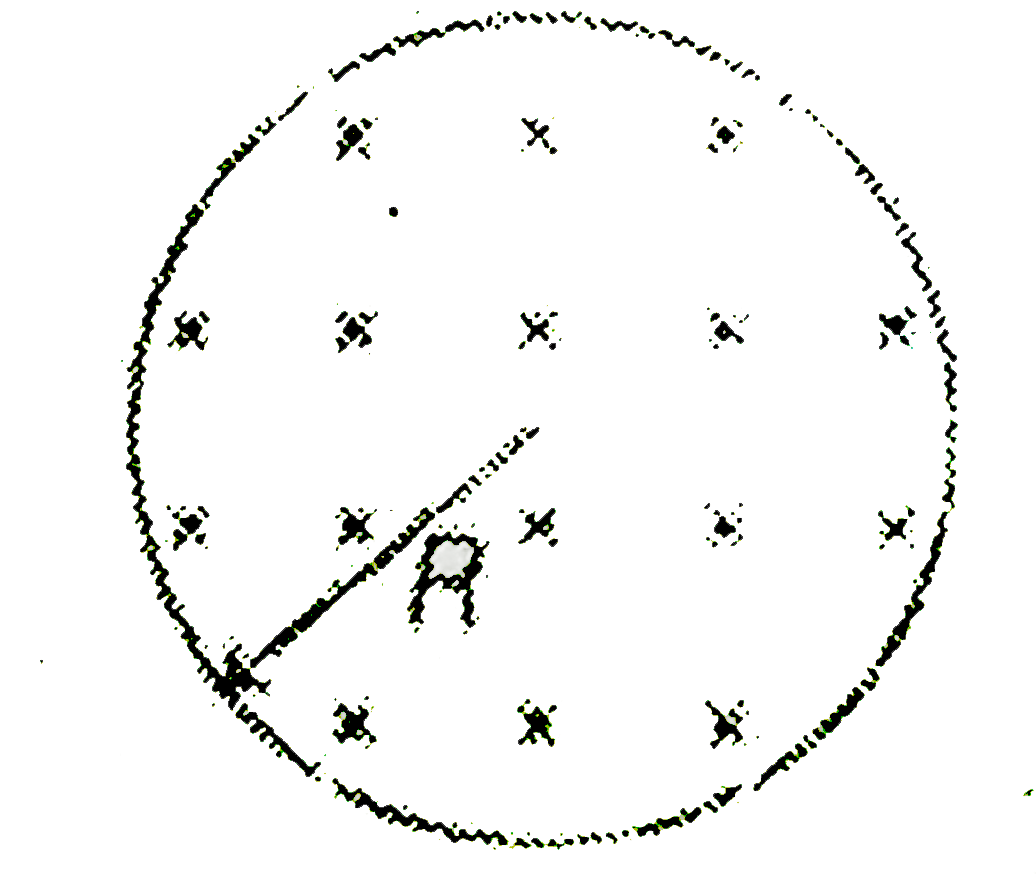 A
A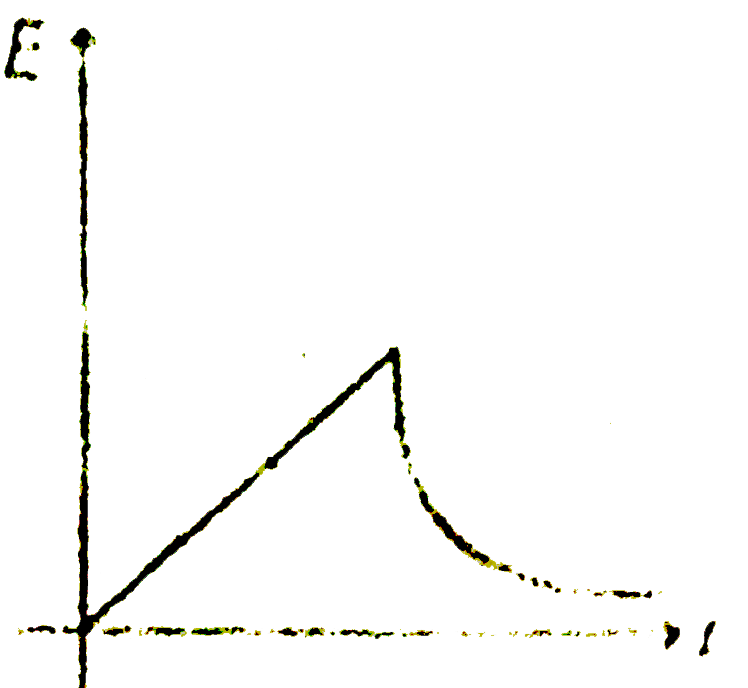 B
B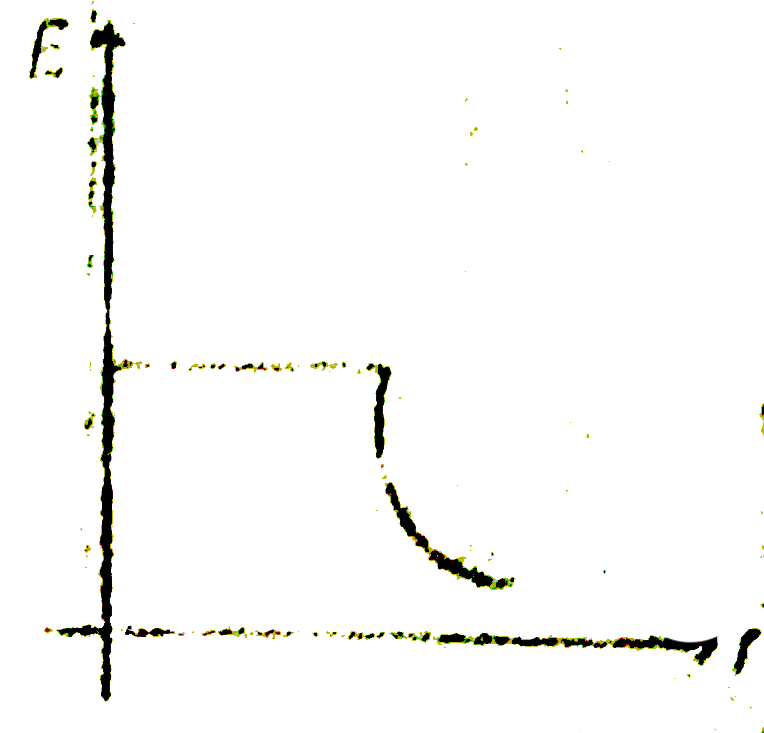 C
C D
D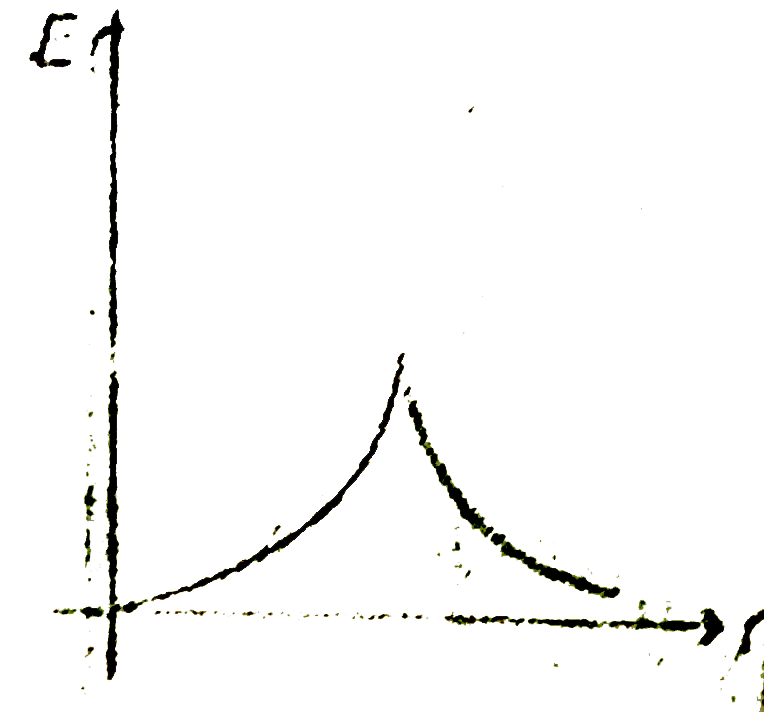
IF two circles of radii r1 and r2 (r2>r1) touch internally , then the distance between their centres will be
Ar1−r2Br2−r1Cr21−r22Dr22−r21
A charge q is placed at the centre of a cylinder of radius R and length 2R. Then electric flux through the curved surface of the cylinder is
View SolutionA long cylinder of radius R1 is displaced along its axis with a constant velocity v0 inside a stationary co-axial cylinder of radius R2. The space between the cylinders is filled with viscous liquid. Find the velocity of the liquid as a function of the distance r from the axis of the cylinders. The flow is laminar.
View SolutionUnder standard conditions helium fills up the space between two long coaxial cylinders. The mean radius of the cylinders is equal to R, the gap between them is equal to ΔR, with ΔR<<R. The outer cylinder rotates with a fairly low angular velocity ω about the stationary inner cylinder. Down to what magnitude should the helium pressure be lowered (keeping the temperature constant) to decrease the sought moment of friction forces n=10 times if ΔR=6mm ?
View SolutionSpace between tow concentric spheres of radii r1andr2 such that r1<r2 is filled with a material of resistivity ρ. Find the resistance between inner and outer surface of the material
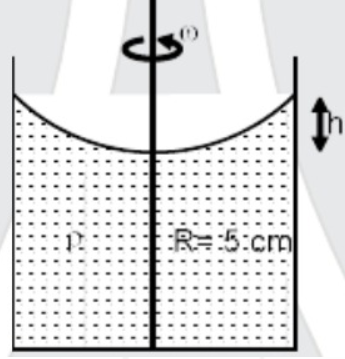
View SolutionA cylindrical container rotates with constant angular speed 'omega = 10 radians/s'. Radius of cylinder is R = 5 cm. Find height h as shown at which water is in equilibrium w.r.t container
View Solution
