Under standard conditions helium fills up the space between two long coaxial cylinders. The mean radius of the cylinders is equal to R, the gap between them is equal to ΔR, with ΔR<<R. The outer cylinder rotates with a fairly low angular velocity ω about the stationary inner cylinder. Down to what magnitude should the helium pressure be lowered (keeping the temperature constant) to decrease the sought moment of friction forces n=10 times if ΔR=6mm ?
In this case
N1r22−r21r21r22=4πηω
or N12RΔRR4≈4πηω or N1=2πηωr3ΔR
To decrease N1,n times η must be decreased n times. Now η does not depend on pressure until the pressure is so low that the mean free path equals, say, 12ΔR. Then the mean free path is fixed and η decreases with pressure. The mean free path equals 12ΔR when
1√2πd2n0=ΔR(n0=concentration)
Corresponding pressure is p0=√2kTπd2ΔR
The sought pressure is n times less
p=√2kTπd2nΔR=70.7×10−2310−18×10−3≈0.71Pa
the answer is qualitative and depends on the choice 12ΔR for the mean free path.
Topper's Solved these Questions
- THERMODYNAMICS AND MOLECULAR PHYSICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:THERMODYNAMICS AND MOLECULAR PHYSICSExercise:Phase Transformations
Explore 35 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:PHYSICAL FUNDAMENTALS OF MECHANICSExercise:Relativistic Mechanics
Explore 49 Videos
Similar Questions
A gas fills up the space between two long coaxial cylinders of radii R1 and R2, with R1<R2. The outer cylinder rotates with a fairly low angular velocity ω about the stationary inner cylinder. The moment of friction forces acting on a unit length of the inner cylinder is equal to N1. Find the viscosity coefficient η of the gas taking into account that the friction force acting on a unit area of the cylindrical surface of radius r is determined by the formule σ=ηr(∂ω/∂r).
View SolutionThe volume of a cylinder whose radius r is equal to its height is
View Solution
Knowledge Check
The relation between length L and radius R of the cylinder , if its moment of inertia about its axis is equal to that about the equatorial axis, will be
AL = RBL = 2RCL = 3RDL=√3RAn cylinder of mass m is rotated about its axis by an angular velocity ω and lowered gently on an inclined plane as shown in figure. Then :
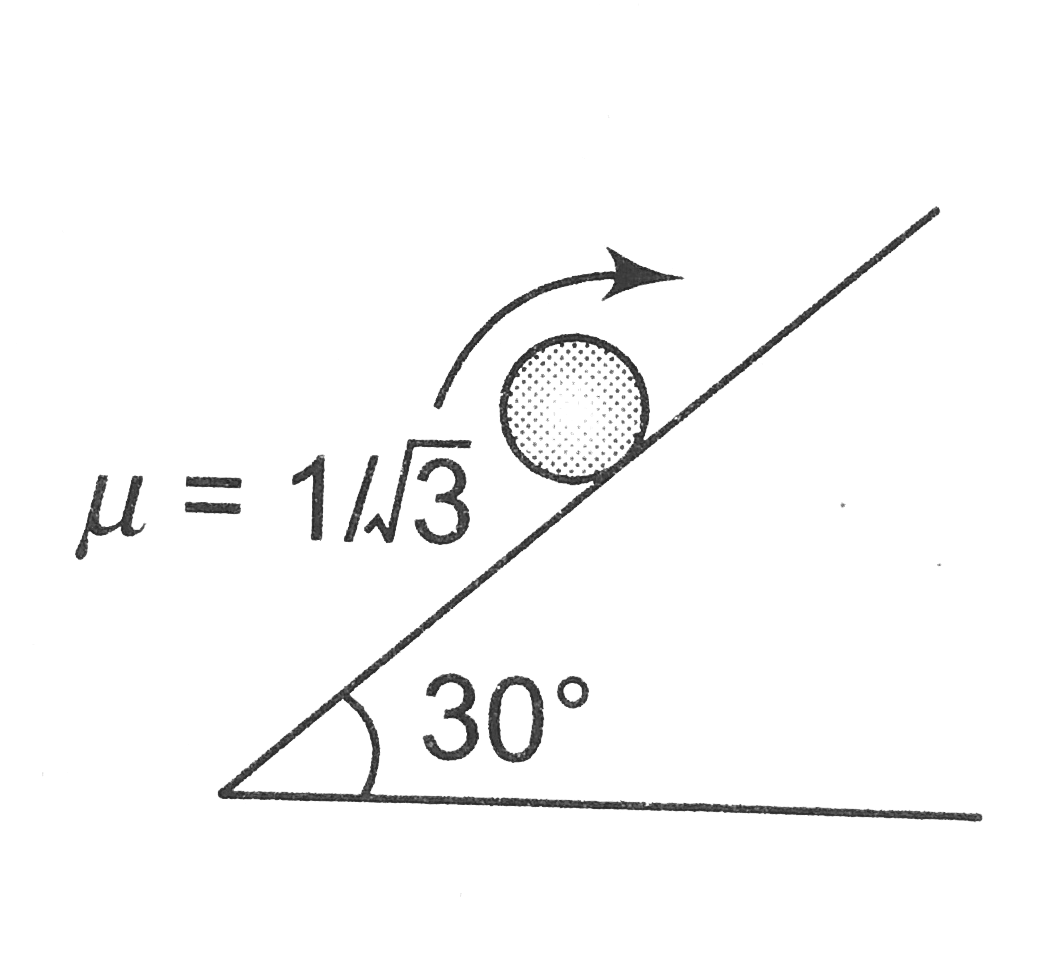 .Ait will start going upwardBit will first going upward and then downwardCit will go downward just after it is loweredDit can never go upward.
.Ait will start going upwardBit will first going upward and then downwardCit will go downward just after it is loweredDit can never go upward.Moment of inertia of a hollow cylinder of mass M and radius R, about the axis of cylinder is
A12MR2BMR2C23MR2D25MR2
A homegoneous poorly condcuting medium of resistivity ρ fills up space between two thin coaxial ideally conducting cylinder is l. The radii of the cylinders are equal to a and b with a<b, the length of each cylinder is l. Neglecting the edge effects , find the resistance of the medium between the cylinders.
View SolutionFind the force per unit area on the surface of a long hollow cylinder carrying uniform current I and radius of the cylinder is R.
View SolutionA cylinder of mass M, radius r1 and lenglth l is kept inside another cylinder of radius r2 and length l. The space between them is filled with a liquid of viscosity η. The inner cylinder starts rotating with angular velocity ω while the other cylinder is at rest. Find time when inner cylinder stops.
View SolutionA solid cylinder of mass M and radius R rotates about its axis with angular speed ω. Its rotational kinetic energy is
View SolutionRadius of a cylinder is equal to the side of an equilateral triangle having area 25√3cm2 and height of the cylinder is equal to the perimeter of the triangle. Then find the volume of cylinder.
View Solution

