A cylinder of mass M, radius r1 and lenglth l is kept inside another cylinder of radius r2 and length l. The space between them is filled with a liquid of viscosity η. The inner cylinder starts rotating with angular velocity ω while the other cylinder is at rest. Find time when inner cylinder stops.
To solve the problem, we will follow these steps:
Step 1: Understand the System
We have two concentric cylinders: an inner cylinder of radius r1 and an outer cylinder of radius r2. The space between them is filled with a viscous liquid of viscosity η. The inner cylinder starts rotating with an angular velocity ω, while the outer cylinder remains at rest.
Step 2: Determine the Viscous Force
The viscous force F acting on the inner cylinder can be expressed using the formula:
F=−ηAdVdy
where:
- A is the area of contact between the liquid and the inner cylinder,
- dVdy is the velocity gradient.
The area A for the curved surface of the inner cylinder is given by:
A=2πr1L
where L is the length of the cylinder.
Step 3: Calculate the Velocity Gradient
The velocity of the liquid at the inner cylinder surface is ωr1, while at the outer cylinder surface (which is at rest) the velocity is 0. The distance between the two surfaces is r2−r1. Thus, the velocity gradient can be expressed as:
dVdy=0−ωr1r2−r1=−ωr1r2−r1
Step 4: Substitute into the Viscous Force Equation
Substituting the area and the velocity gradient into the viscous force equation, we get:
F=−η(2πr1L)(−ωr1r2−r1)=2πηLωr21r2−r1
Step 5: Calculate the Torque
The torque τ due to the viscous force is given by:
τ=F⋅r1=2πηLωr21r2−r1⋅r1=2πηLωr31r2−r1
Step 6: Relate Torque to Angular Deceleration
According to Newton's second law for rotation, we have:
τ=Iα
where I is the moment of inertia of the inner cylinder and α is the angular acceleration. The moment of inertia I for a solid cylinder is given by:
I=12Mr21
Thus, we can write:
2πηLωr31r2−r1=12Mr21dωdt
Step 7: Rearranging the Equation
Rearranging gives:
dωdt=−4πηLωM(r2−r1)
Step 8: Integrate to Find Time
We can separate variables and integrate:
∫dωω=−4πηLM(r2−r1)∫dt
Integrating gives:
lnω=−4πηLM(r2−r1)t+C
At t=0, ω=ω0, so:
C=lnω0
Thus, we have:
lnω=−4πηLM(r2−r1)t+lnω0
Step 9: Solve for Time t
Rearranging gives:
t=−M(r2−r1)4πηL(lnω−lnω0)=M(r2−r1)4πηLlnω0ω
When the inner cylinder stops, ω=0, thus:
t=M(r2−r1)4πηLlnω00
This indicates that the time taken to stop is theoretically infinite as ω approaches zero.
Final Result
The time taken for the inner cylinder to stop is given by:
t=M(r2−r1)4πηLlnω0ω
We have two concentric cylinders: an inner cylinder of radius r1 and an outer cylinder of radius r2. The space between them is filled with a viscous liquid of viscosity η. The inner cylinder starts rotating with an angular velocity ω, while the outer cylinder remains at rest.
The viscous force F acting on the inner cylinder can be expressed using the formula:
F=−ηAdVdy
where:
- A is the area of contact between the liquid and the inner cylinder,
- dVdy is the velocity gradient.
A=2πr1L
where L is the length of the cylinder.
The velocity of the liquid at the inner cylinder surface is ωr1, while at the outer cylinder surface (which is at rest) the velocity is 0. The distance between the two surfaces is r2−r1. Thus, the velocity gradient can be expressed as:
dVdy=0−ωr1r2−r1=−ωr1r2−r1
Substituting the area and the velocity gradient into the viscous force equation, we get:
F=−η(2πr1L)(−ωr1r2−r1)=2πηLωr21r2−r1
The torque τ due to the viscous force is given by:
τ=F⋅r1=2πηLωr21r2−r1⋅r1=2πηLωr31r2−r1
According to Newton's second law for rotation, we have:
τ=Iα
where I is the moment of inertia of the inner cylinder and α is the angular acceleration. The moment of inertia I for a solid cylinder is given by:
I=12Mr21
Thus, we can write:
2πηLωr31r2−r1=12Mr21dωdt
Rearranging gives:
dωdt=−4πηLωM(r2−r1)
We can separate variables and integrate:
∫dωω=−4πηLM(r2−r1)∫dt
Integrating gives:
lnω=−4πηLM(r2−r1)t+C
At t=0, ω=ω0, so:
C=lnω0
Thus, we have:
lnω=−4πηLM(r2−r1)t+lnω0
Rearranging gives:
t=−M(r2−r1)4πηL(lnω−lnω0)=M(r2−r1)4πηLlnω0ω
When the inner cylinder stops, ω=0, thus:
t=M(r2−r1)4πηLlnω00
This indicates that the time taken to stop is theoretically infinite as ω approaches zero.
The time taken for the inner cylinder to stop is given by:
t=M(r2−r1)4πηLlnω0ω
Topper's Solved these Questions
- SURFACE TENSION & VISCOSITY Book:MOTIONChapter:SURFACE TENSION & VISCOSITY Exercise:Exercise - 1 Objective Problems | JEE Main
Explore 19 Videos
- SURFACE TENSION & VISCOSITY Book:MOTIONChapter:SURFACE TENSION & VISCOSITY Exercise:Exercise - 2 (Level-I) Objective Problems | JEE Main
Explore 11 Videos
- SURFACE TENSIONBook:MOTIONChapter:SURFACE TENSIONExercise:Exercise - 3 | Section - B Previous Year Problems | AIEEE
Explore 12 Videos
- ThermodynamicsBook:MOTIONChapter:ThermodynamicsExercise:EXERCISE - 3 SECTION b
Explore 26 Videos
Similar Questions
A long cylinder of radius R1 is displaced along its axis with a constant velocity v0 inside a stationary co-axial cylinder of radius R2. The space between the cylinders is filled with viscous liquid. Find the velocity of the liquid as a function of the distance r from the axis of the cylinders. The flow is laminar.
View SolutionTwo cylinders having radiii R1 and R2 and rotational inertia I1 and I2 respectively, are supported by fixed axes perpendicular to the plane of figure-5.52. The large cylinder is initially rotating with angular velocityω0. The small cylinder is moved to the right until it touches the large cylinder and is caused to rotate by the frictional force between the two. Eventually, slipping ceases, and the two cylinders rotate at constant rates in opposite directions, (a) Find the final angular velocity ω2 of the small cylinder in terms of I1,I2,R1,R2 and ω0. (b) Is total angular momentum conserved in this case ?
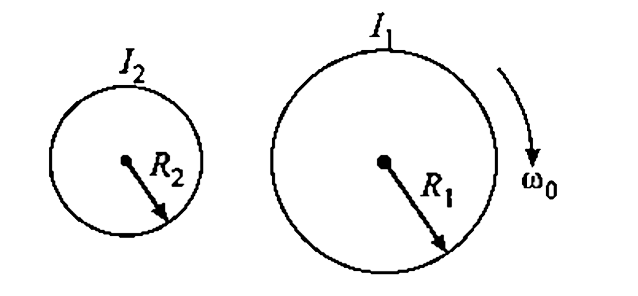
View Solution
Knowledge Check

There are two concentric cylinders of radii R1 and R2 as shown. The narrow space between the two cylinders is filled with liquid of viscosity μ. The inner cylinder is held stationary by means of a torsional spring of stiffness G. the outer cylinder is rotated with constant angular speed ω. The torque acting on the inner cylinder due to shearing action of thhe liquid:AπμωR42h+2πμωHR21R2R2−R1BπμωHR21R2R2−R1CπμωHR21R2R2−R1+μωR43hDπμωR42hTwo smooth sphere each of radius 5cm and weight W rest one on the other inside a fixed smooth cylinder of radius 8cm. The reaction between the sphere and the vertical side of the cylinder are:
 AW/4 and 3W/4BW/4 and W/4C3W/4 and 3W/4DW and W
AW/4 and 3W/4BW/4 and W/4C3W/4 and 3W/4DW and WA cylinder of radius R and length L is placed in a uniform electric field E parallel to the axis. The total flux for the surface of the cylinder is given by
A2πR2EBπR2/EC(πR2/πR)/EDZero
What is moment of inertia of a solid cylinder of mass m, length l and radiusr about the axis of the cylinder ?
View SolutionUnder standard conditions helium fills up the space between two long coaxial cylinders. The mean radius of the cylinders is equal to R, the gap between them is equal to ΔR, with ΔR<<R. The outer cylinder rotates with a fairly low angular velocity ω about the stationary inner cylinder. Down to what magnitude should the helium pressure be lowered (keeping the temperature constant) to decrease the sought moment of friction forces n=10 times if ΔR=6mm ?
View SolutionA cylinder of radius r and length l is placed in an uniform electric field parallel to the axis of the cylinder. The total flux for the surface of the cylinder is given by-
View SolutionA cylinder of radius R and length L is placed in a uniform electric field E parallel to the axis. The total flux for the surface of the cylinder is given by
View SolutionA cylinder of radius R and length l is placed in a uniform electric field E parallel to the axis of the cylinder. The total flux over the curved surface of the cylinder is
View Solution

