A homegoneous poorly condcuting medium of resistivity ρ fills up space between two thin coaxial ideally conducting cylinder is l. The radii of the cylinders are equal to a and b with a<b, the length of each cylinder is l. Neglecting the edge effects , find the resistance of the medium between the cylinders.
Let us mentally isolate a thin cylindrical layer of inner and outer radii r and r+dr respectively. As lines of current at all the points of this layer are perpendicular to it, such a layer can be treated as a cylindrical conductor of thickness dr and cross-sectional area 2πrl. So, we have
dR=ρdrS(r)=ρdr2πrl
and intergating between the limits, we get,
R=ρ2πrlInba

Topper's Solved these Questions
- ELECTRODYNAMICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:ELECTRODYNAMICSExercise:Constant Magnetic Fiels - Magnetics
Explore 69 Videos
- ELECTRODYNAMICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:ELECTRODYNAMICSExercise:Electromagnetic Induction
Explore 84 Videos
- ELECTRODYNAMICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:ELECTRODYNAMICSExercise:Electric Capacitance - Energy Of An Electric Field
Explore 46 Videos
- ELECTRICITY AND MAGNETISMBook:IE IRODOV, LA SENA & SS KROTOVChapter:ELECTRICITY AND MAGNETISMExercise:All Questions
Explore 6 Videos
- ELECTROMAGNETISMBook:IE IRODOV, LA SENA & SS KROTOVChapter:ELECTROMAGNETISMExercise:All Questions
Explore 24 Videos
Similar Questions
A metal ball of radius a is located at a distance l from an indinite ideally conducting plane. The space around the ball is filled with a homongeous poorly conducting medium with resistivity ρ. In the case of a<<l find :
(a) the current density at the conducting plane as a function of distance r from the ball if the potentail difference between the ball and the plane is equal to V ,
(b) the electric resistance of the medium between the balll and the plane.
View SolutionTwo long parallel wires are located in a poorly conducting medium with respectivity ρ. The distance between the axes of the wires is equal to l, the cross -section radius of each wire equals a. In the case a<<l find,
(a) the current density at the point equally removed from the axes of the wire by a distance r if the potential difference between teh wires is equal to V,
(b) the electric resistances of the medium per unit length of the wires.
View Solution
Knowledge Check
A cylinder of length L and radius b has its axis coincident with x-axis. The electric field in this region is →E=200ˆi. Find the flux through the left end of the cylinder.
A0B200πb2C100πb2D−200πb2A copper cylindrical tube has inner radius a and outer radius b. The resistivity is ρ. The resistance of the cylinder between the two ends is
Aρlb2−a2Bρl2π(b−a)Cρlπ(b2−a2)Dπ(b2−a2)ρl
A conductor having resistivity ρ is bent in the shape of a half cylinder as shown in the figure. The inner and outer radii of the cylinder are aandb respectively and the height of the cylinder is h. A potential difference is applied across the two rectangular faces of the conductor. Calculate the resistance offered by the conductor.
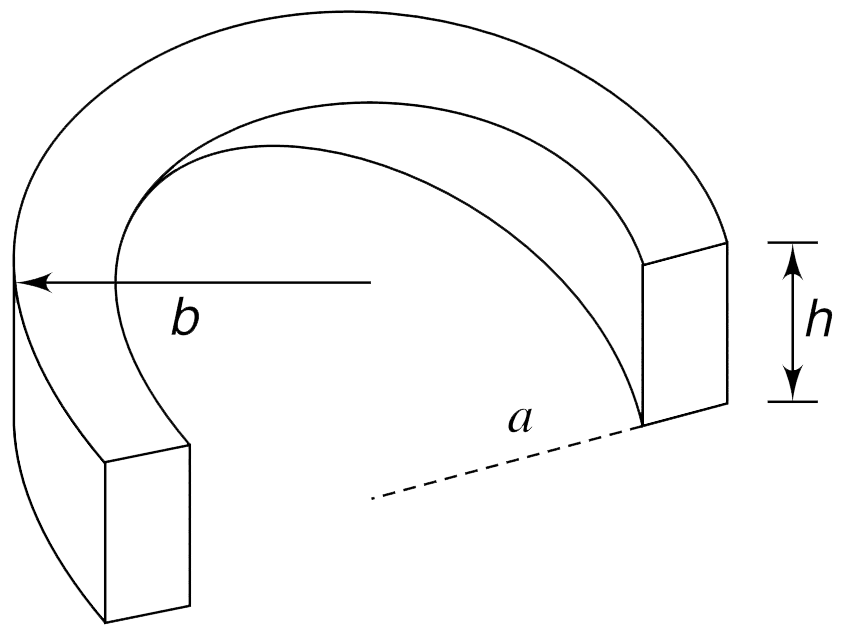
View SolutionFind the self inductance of a unit length of a cable consisting of two thin walled coaxial metallic cylinders if the radius of the outside cylinder is η(η>1) times that of the inside one. The permeability of the medium between the cylinders is assumed to be equal to unity.
View SolutionUnder standard conditions helium fills up the space between two long coaxial cylinders. The mean radius of the cylinders is equal to R, the gap between them is equal to ΔR, with ΔR<<R. The outer cylinder rotates with a fairly low angular velocity ω about the stationary inner cylinder. Down to what magnitude should the helium pressure be lowered (keeping the temperature constant) to decrease the sought moment of friction forces n=10 times if ΔR=6mm ?
View SolutionA thin straight infinitely long conducting wire having charge density λ is enclosed by a cylinder surface of radius r and length l, its axis coinciding with the length of the wire. Find the expression for the electric flux through the surface of the cylinder.
View SolutionFind the inductance of a unit length of a cable consisting of two thin-walled coaxial metallic cylinders if the radius of the outside cylinder is η=3.6 times that of the inside one. The permeabitity of a medium between the cylinders is assumed to be equal to unity.
View SolutionFigure shown a section through two long thin concentric cylinders of radii a & b with a>b. The cylinders have equal and opposite per unit length λ. Find the electric field at a distance r from the axis for (i) r<a (ii) a<r<b (iii) r>b

View Solution

