There is an infinite wire grid with square cells (Fig). The resistance of each wire between neighbouring joint connections is equal to R0 . Find the resistance R of the whole grid between points A and B.
Instruction. Make use of principles of symmetry and superposition.

Suppose that the voltage V is applied between the points A and B then
V=IR=I0R0
where R is resistance of whole the grid I, the current through the grid and I0 the current through the segment AB. Now from symmetry , I/4 is the part of the current, flowing through all the four wire segments, meeting at the poin A and similarly the amount of current flowing through the wires, meeting at B is also I/4. Thus a current 1/2 flows through the conductor AB, ie.
I0=12
Hence, R=R02
Topper's Solved these Questions
- ELECTRODYNAMICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:ELECTRODYNAMICSExercise:Constant Magnetic Fiels - Magnetics
Explore 69 Videos
- ELECTRODYNAMICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:ELECTRODYNAMICSExercise:Electromagnetic Induction
Explore 84 Videos
- ELECTRODYNAMICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:ELECTRODYNAMICSExercise:Electric Capacitance - Energy Of An Electric Field
Explore 46 Videos
- ELECTRICITY AND MAGNETISMBook:IE IRODOV, LA SENA & SS KROTOVChapter:ELECTRICITY AND MAGNETISMExercise:All Questions
Explore 6 Videos
- ELECTROMAGNETISMBook:IE IRODOV, LA SENA & SS KROTOVChapter:ELECTROMAGNETISMExercise:All Questions
Explore 24 Videos
Similar Questions
Knowledge Check
There is an infinite wire grid with cells in the form of equilateral triangles. The resistance of each wire between neighboring joint connections is R0 The net resistance of the whole grid between the points A and B as shown in fig.
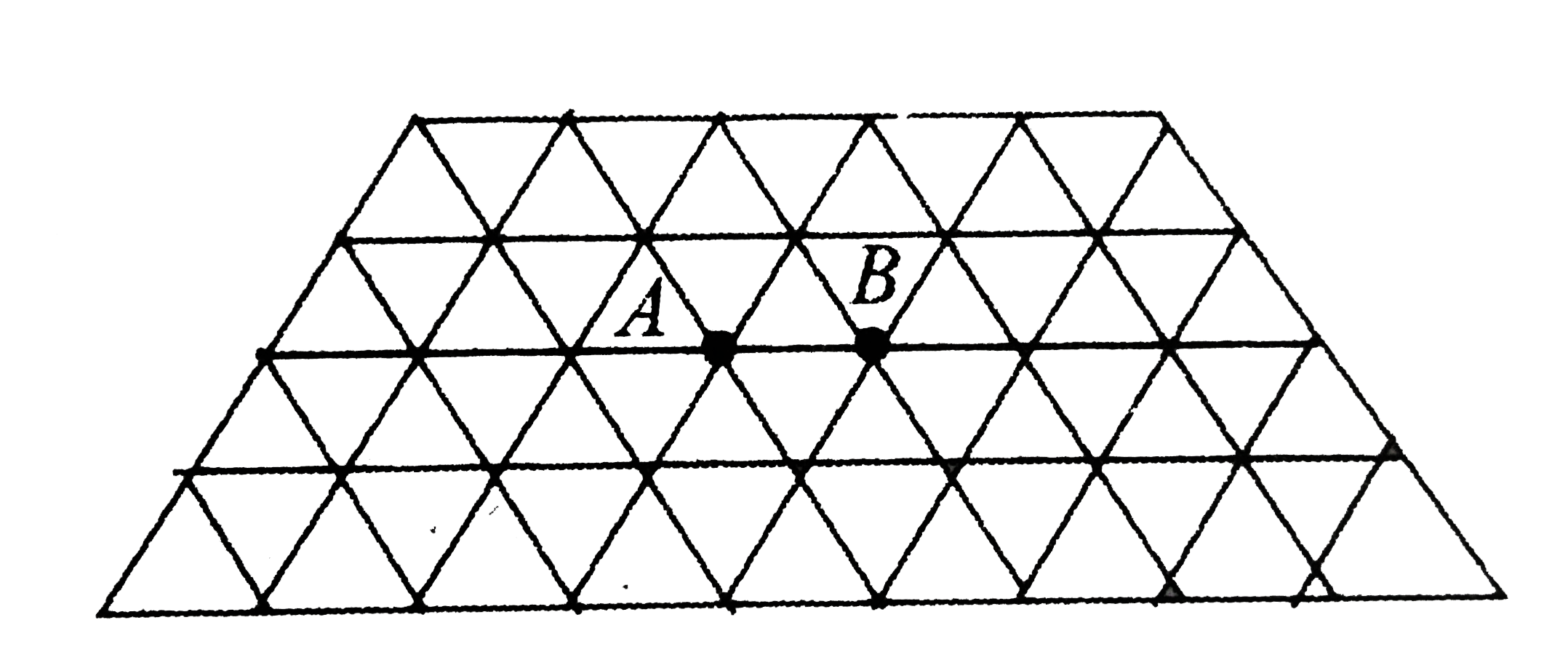 AR0BR02CR02DR03
AR0BR02CR02DR03In the circuit shown in figure the total resistance between points A and B is R0. The value of resistance R is
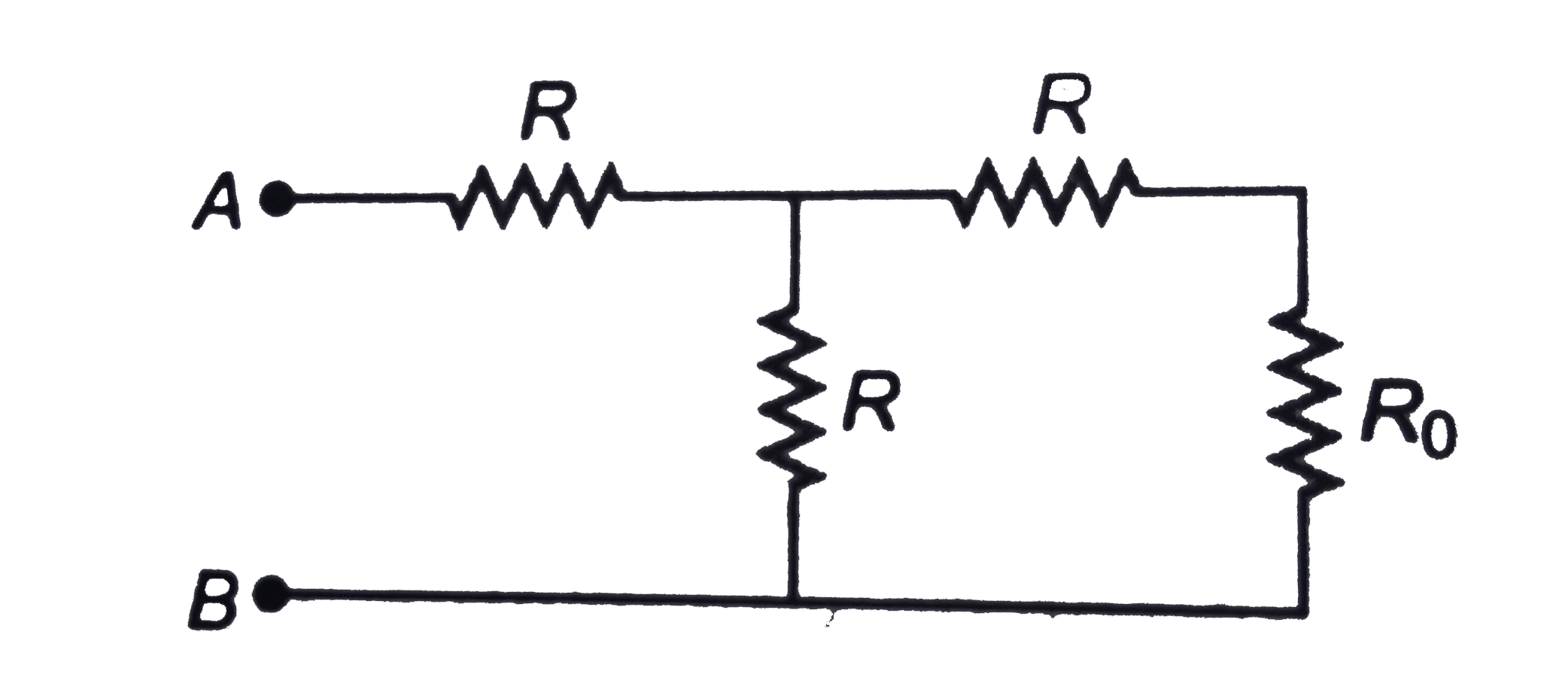 AR0B√3R0CR02DR0√3
AR0B√3R0CR02DR0√3The resistance of all the wires between any two adjacent dots is R. Then equivalent resistance between A and B as shown in figure
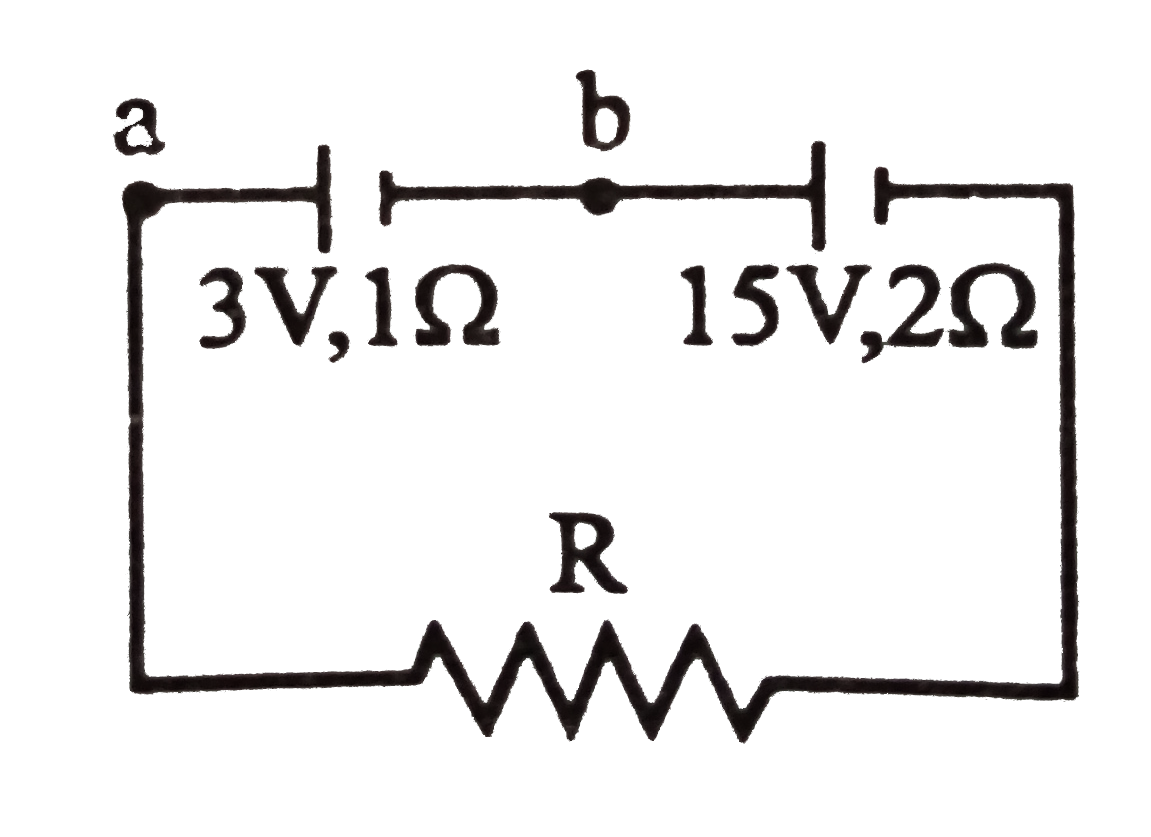 A5B7C3D1
A5B7C3D1
Find the equivalent resistance of the circuits shown in figure between the points a and b. Each resistor has a resistance r.


View SolutionFind the equivealent resistance of the circuit shown in Fig. 4.61 between the points P and Q. Each resistor has a resistance r.
View SolutionFig. shows an infinite circuit formed by the repetition of the same link, consisting of resistance R1=4.0Ω and R2=3.0Ω. Find the resistance of this circuit between points A and B.

View SolutionFind equivalent resistance between points A and B in the circuit shown. All resistances are equal toR.
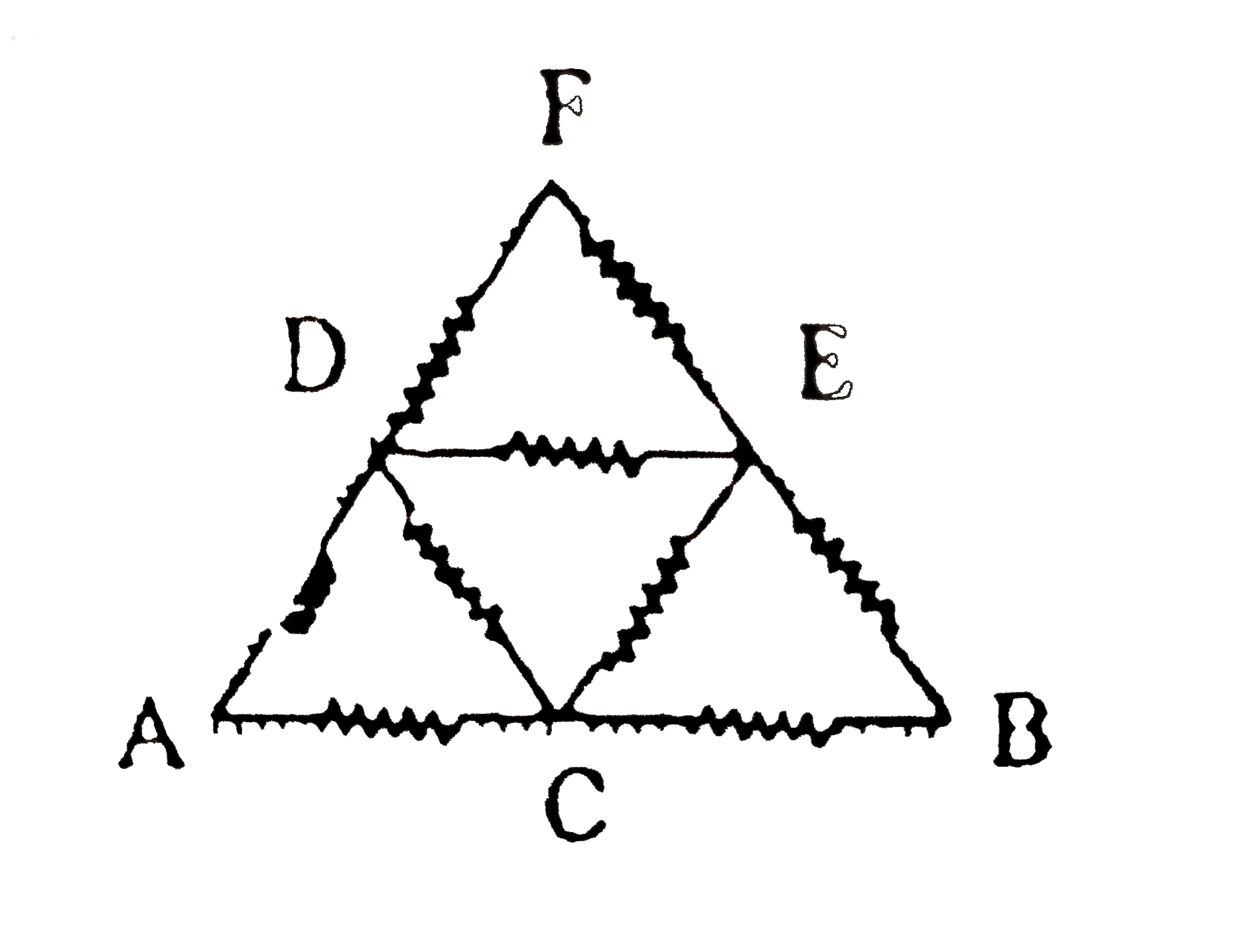
View SolutionThe resistance of all the wires between any two adjacent dots is R. Then, equivalent resistance between Aand B as shown in figure is

View Solution



