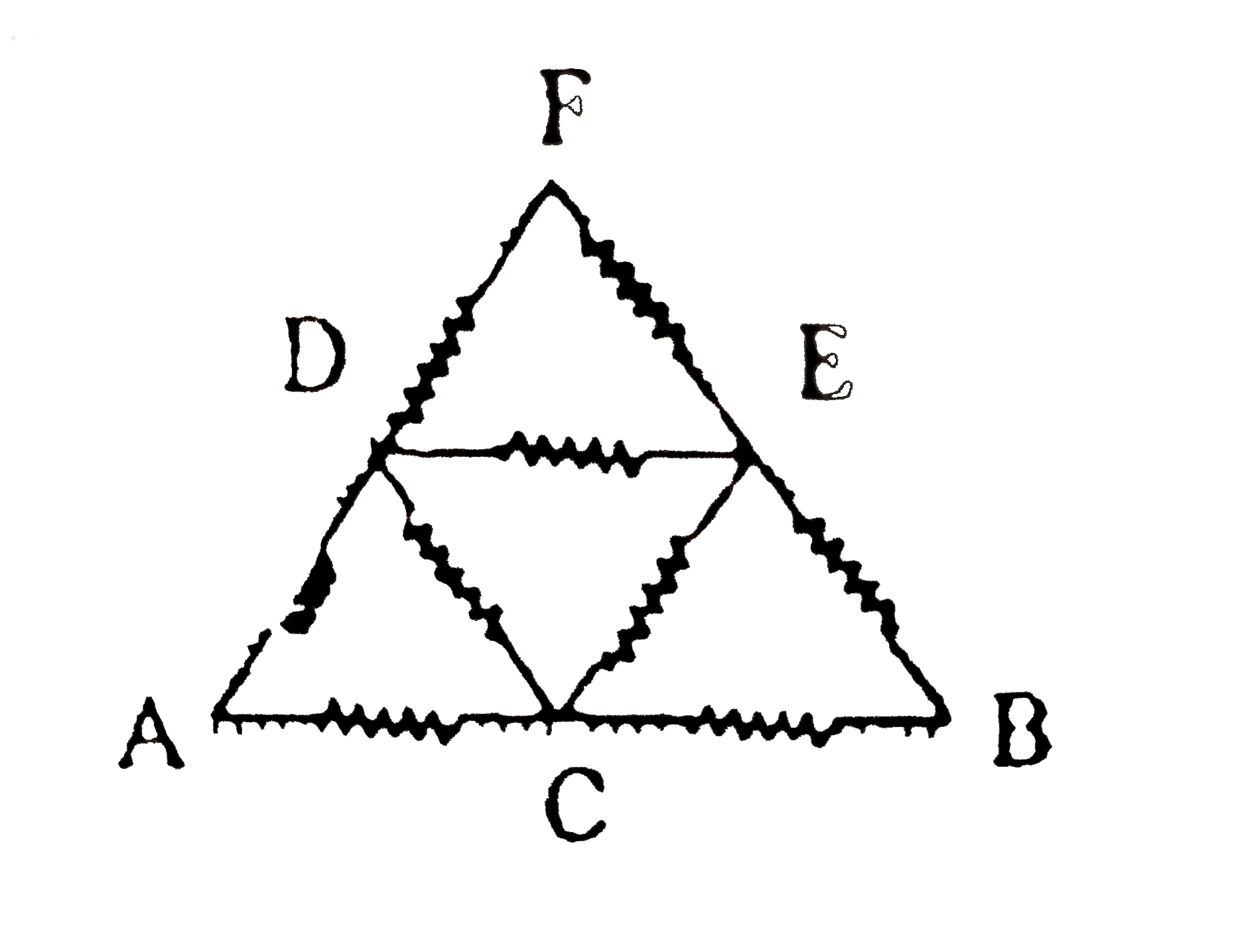
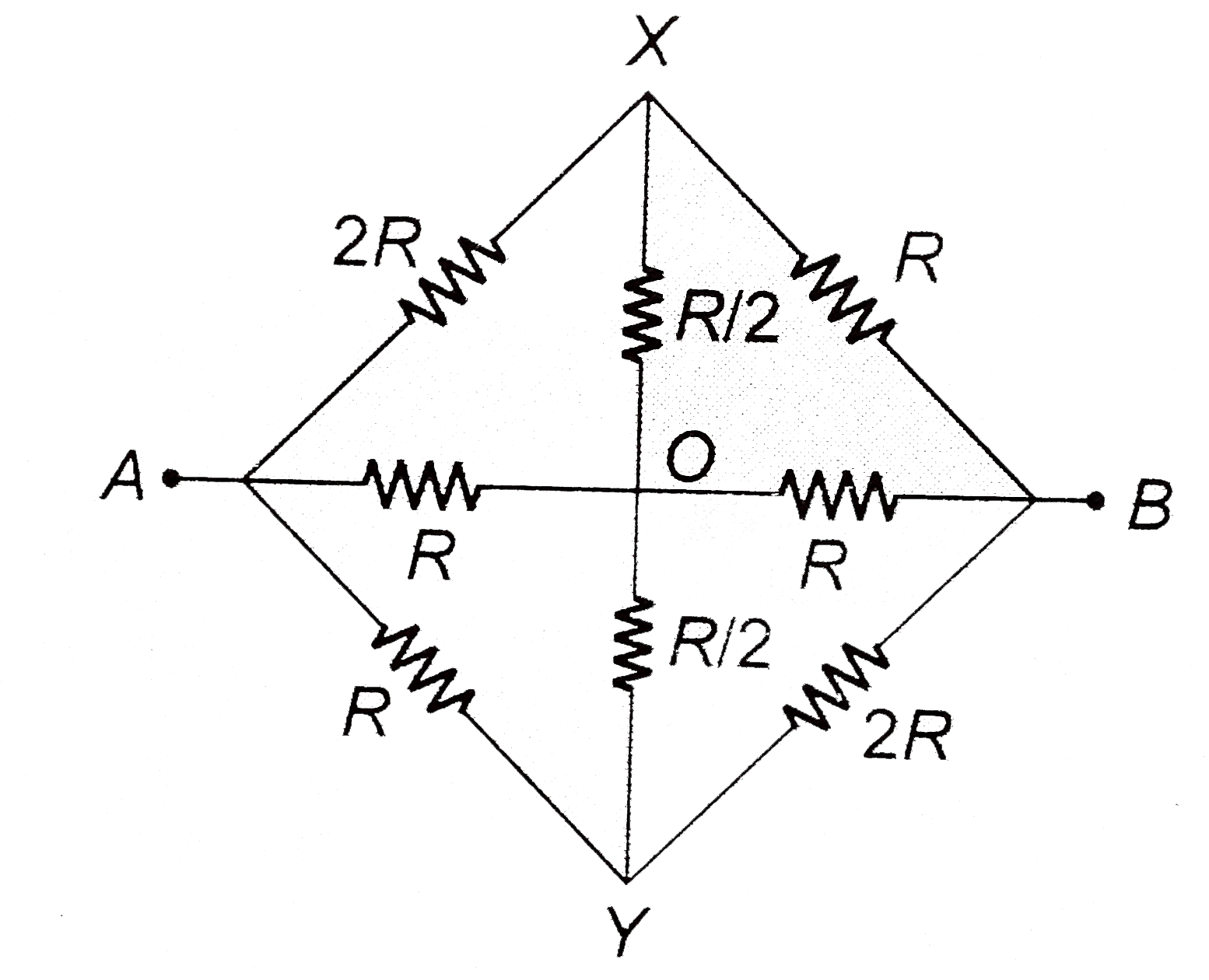
Find equivalent resistance between points A and B in the circuit shown. All resistances are equal toR.
Video Solution
Text Solution
We will solve this using symmetry about the dotted line. From this we can deduce that the centre in a branch will be equal to the current in its mirror image. For example current in AC= current in CB=i1.
This implies that even if we break the junction at C, the currents in the circuit will not be affected. Now, the circuit is simplified which can be easily solved using series parallel combination.
RAB=2R in parallel to (2R+R2)=109R
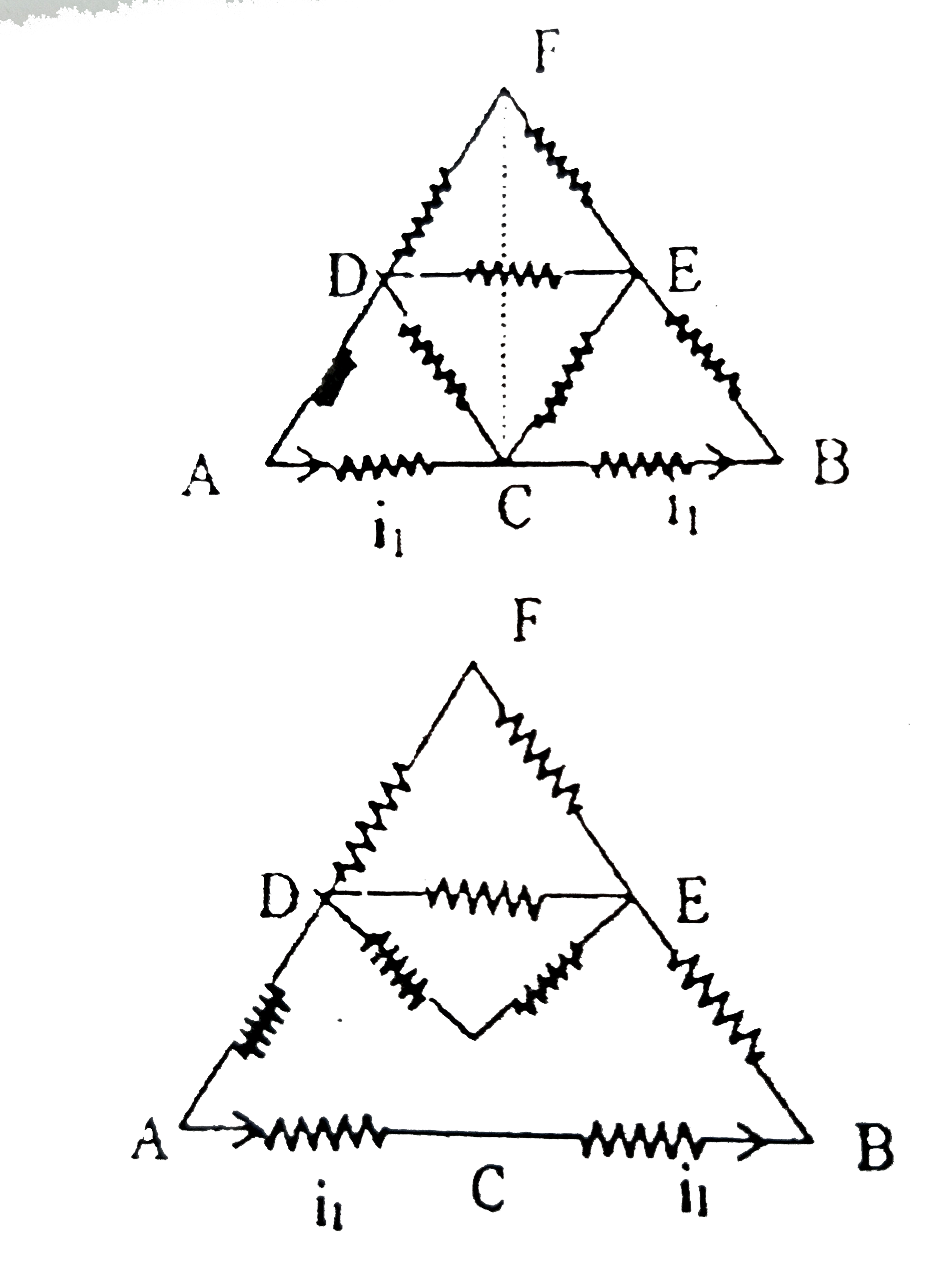
|
Topper's Solved these Questions
- CURRENT ELECTRICITYBook:FIITJEEChapter:CURRENT ELECTRICITYExercise: Illustration
Explore 10 Videos
- CURRENT ELECTRICITYBook:FIITJEEChapter:CURRENT ELECTRICITYExercise:SOLVED PROBLEMS (SUBJECTIVE)
Explore 10 Videos
- COLLISION Book:FIITJEEChapter:COLLISION Exercise:(NUMERICAL BASED QUESTIONS)
Explore 4 Videos
- ELASTICITY AND WAVES Book:FIITJEEChapter:ELASTICITY AND WAVES Exercise:Assignment Problems (Objective) Level-II
Explore 15 Videos
Similar Questions
Knowledge Check
Find the equivalent resistance between points A and B in the following circuit
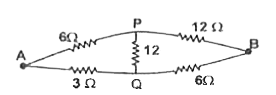 A6ΩB12ΩC4ΩD18Ω
A6ΩB12ΩC4ΩD18ΩFind the equivalent resistance between the points a and b
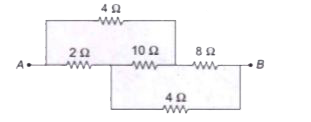 A2ΩB4ΩC8ΩD16Ω
A2ΩB4ΩC8ΩD16Ω
The equivalent resistance between points A and B in the given circuit is
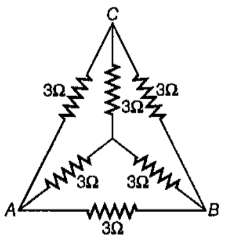
View SolutionEquivalent resistance between points A & B in the given circuit is
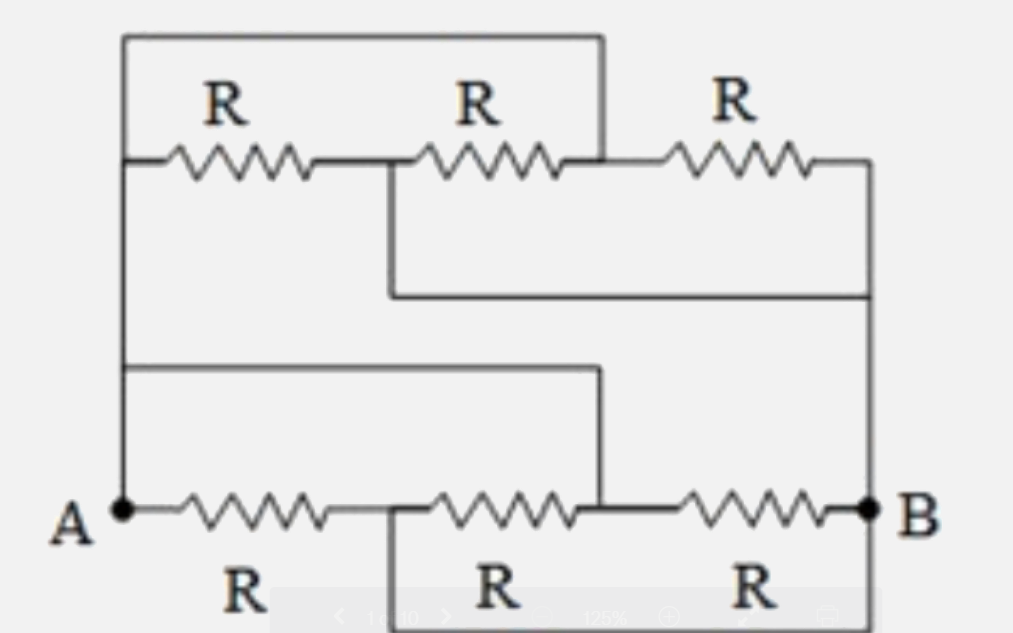
View SolutionEquivalent resistance between points A & B in the given circuit is

View SolutionWhat is the equivalent resistance between points A and B in the circuit.
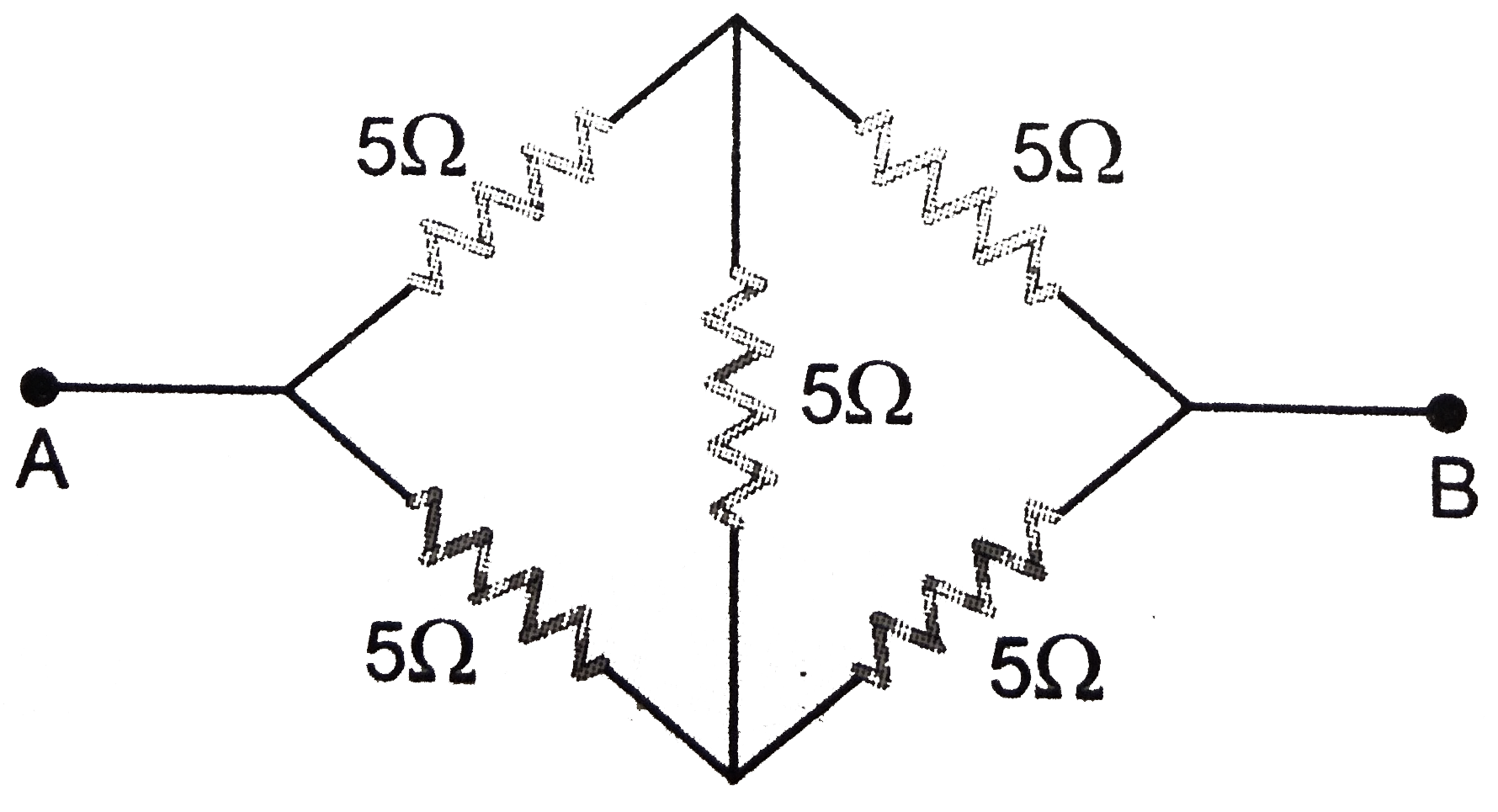
View SolutionFind the the equivalent resistance between points A and B.
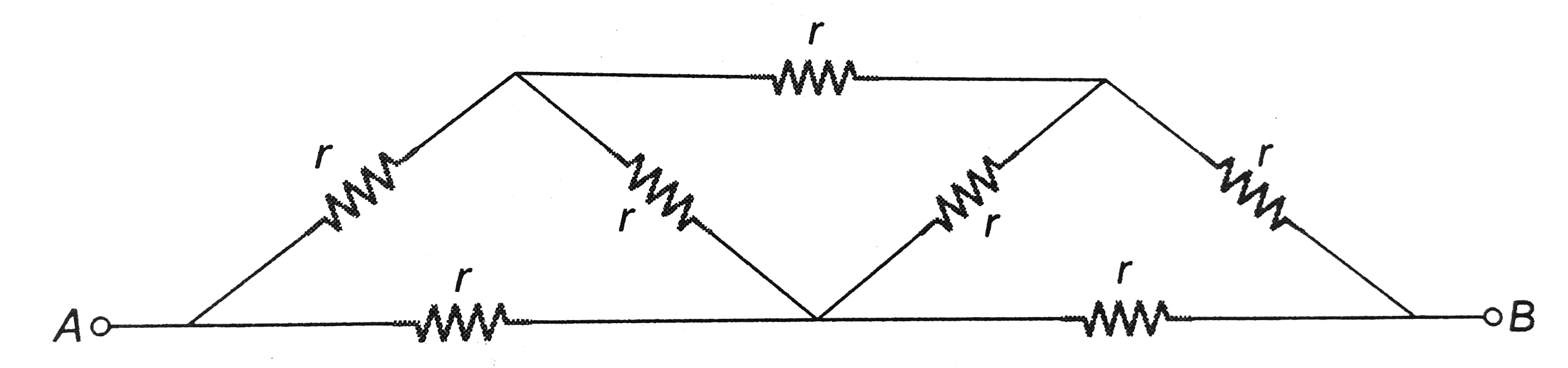
View SolutionFind the equivalent resistance between the points A and B.
 .
.
View Solution


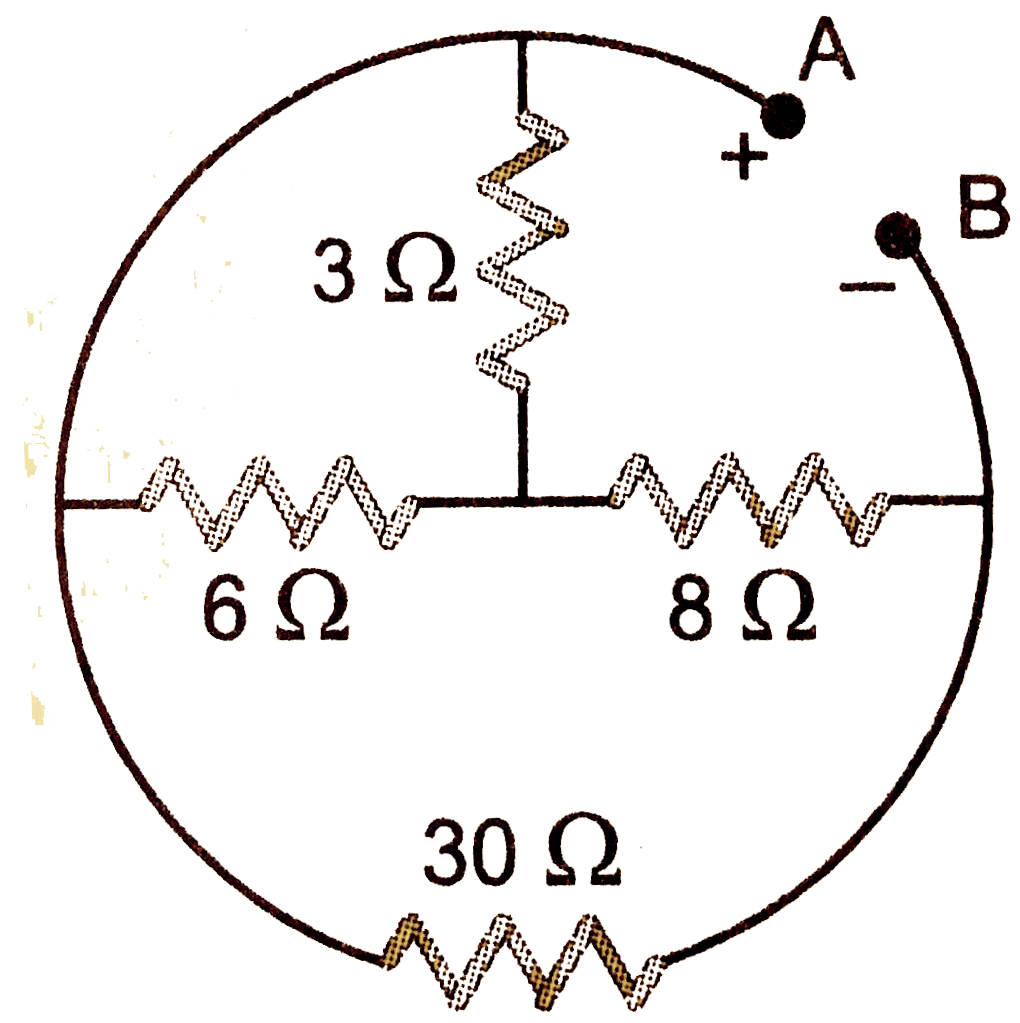
_PHY_E05_095_Q01.png)