Making use of Poiseuille's equation $(1.7 d)$ , find the mass $μ$ of gas flowing per unit time through the pipe of length $l$ and radius $a$ if constant pressures $p_{1}$ and $p_{2}$ are maintained at its ends.

Video Solution

Text Solution

Verified by Experts

Take an infinitesimal section of length $d x$ and apply Poiseuilles equation to this. Then
$\frac{d V}{d t} = \frac{- π a^{4}}{8 η} \frac{\partial p}{\partial x}$
From the formula $p V = R T . \frac{m}{M}$
$p d V = \frac{R T}{M} d m$
or $\frac{d m}{d t} = μ = - \frac{π a^{4} M}{8 η R T} \frac{p d p}{d x}$
This equation implies that if the flow is isothermal then $p \frac{d p}{d x}$ must be a constant and so equals $\frac{∣ ∣ p_{2}^{2} - p_{1}^{2} ∣ ∣}{2 l}$ in magnitude.
Thus, $μ = \frac{π a^{4} M}{16 η R T} \frac{∣ ∣ p_{2}^{2} - p_{1}^{2} ∣ ∣}{l}$ .

Updated on:21/07/2023

If Q is the rate of flow of liquid through a capillary tube of length l and radius r at constant pressure P, then the rate of flow of liquid through a capillary head is
A $\frac{Q}{162}$
B $\frac{Q}{32}$
C $\frac{Q}{64}$
D $\frac{Q}{81}$
For V versus T curves at constant pressure $P_{1} and P_{2}$ for and ideal gas shown in figure-
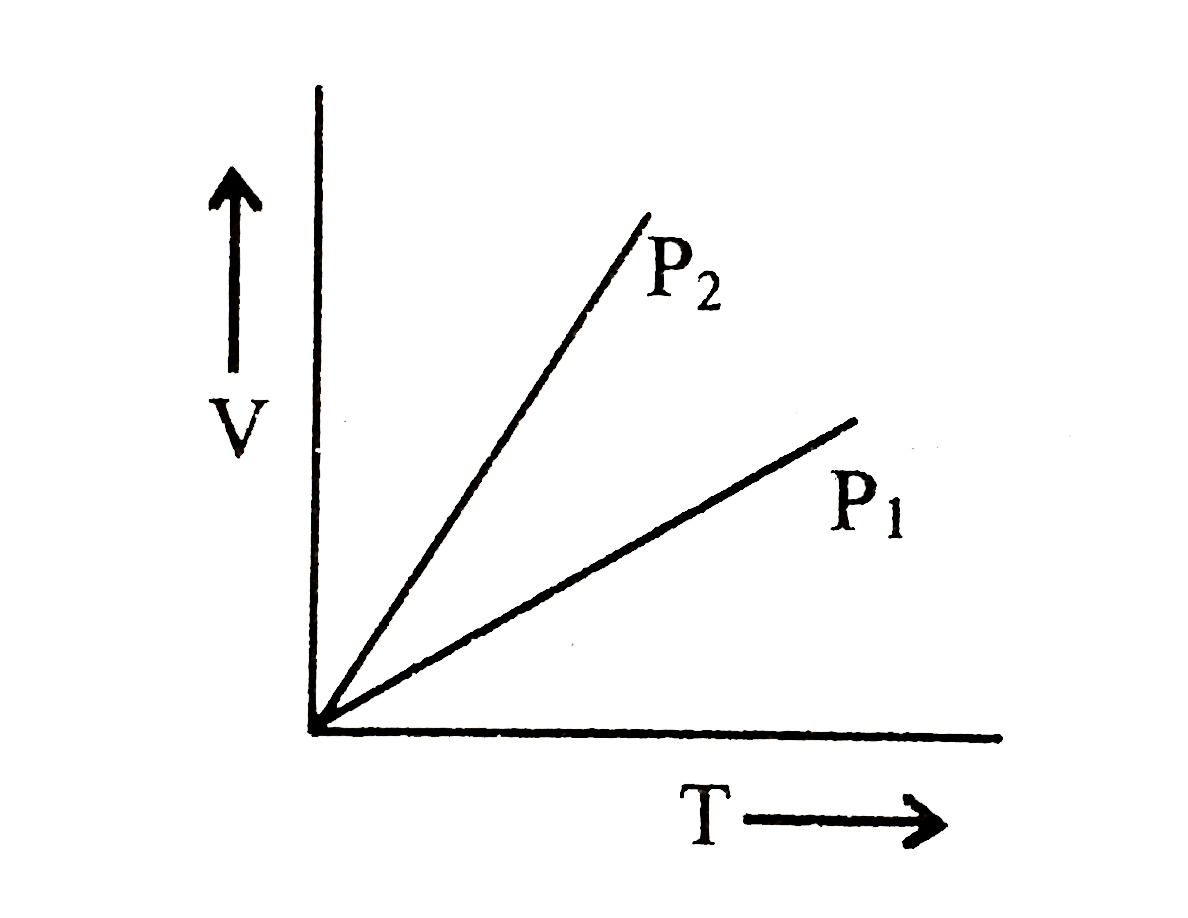A $P_{1} > P_{2}$
B $P_{1} < P_{2}$
C $P_{1} = P_{2}$
D $P_{1} P_{2}$
The volume of a liquid of density $ρ$ and viscosity $η$ flowing in time t through a capillary tube of length l and radius R, with a pressure difference P, across its ends is proportional to :
A $P^{2} R^{2} t / η l^{2}$
B $P R^{4} / η l t$
C $P R^{4} t / η l$
D $η R^{4} / l t$