There is a conducting wire of length l and radius of cross section r. The number of free electrons per unit volume of the conductor is n and the mobility of electrons is μ. A battery of potential difference V is connected across its length. Find electric current flowing through the wire. Assume e as the magnitude of charge on electron.
To find the electric current flowing through the conducting wire, we can follow these steps:
Step 1: Understand the relationship between current, charge, and time
The electric current I is defined as the charge Q flowing through a cross-section of the wire per unit time t:
I=Qt
Step 2: Calculate the charge flowing through the wire
The charge Q can be expressed in terms of the number of free electrons, their charge, and the volume of the wire. The total charge Q can be calculated as:
Q=n⋅Vwire⋅e
where:
- n is the number of free electrons per unit volume,
- Vwire is the volume of the wire,
- e is the charge of an electron.
Step 3: Calculate the volume of the wire
The volume Vwire of the wire can be calculated using its length l and the cross-sectional area A:
Vwire=A⋅l
For a wire with a circular cross-section, the area A is given by:
A=πr2
Thus,
Vwire=πr2⋅l
Step 4: Substitute the volume into the charge equation
Substituting Vwire into the charge equation gives:
Q=n⋅(πr2⋅l)⋅e
Step 5: Relate electric field to potential difference
The electric field E in the wire can be related to the potential difference V and the length l of the wire:
E=Vl
Step 6: Calculate the drift velocity
The drift velocity vd of the electrons can be expressed in terms of mobility μ and electric field E:
vd=μ⋅E=μ⋅Vl
Step 7: Determine the current using drift velocity
The current I can also be expressed in terms of the drift velocity and the cross-sectional area:
I=n⋅A⋅e⋅vd
Substituting A=πr2 and vd=μ⋅Vl into the equation gives:
I=n⋅(πr2)⋅e⋅(μ⋅Vl)
Step 8: Final expression for the current
Thus, the final expression for the electric current flowing through the wire is:
I=n⋅πr2⋅e⋅μ⋅Vl
The electric current I is defined as the charge Q flowing through a cross-section of the wire per unit time t:
I=Qt
The charge Q can be expressed in terms of the number of free electrons, their charge, and the volume of the wire. The total charge Q can be calculated as:
Q=n⋅Vwire⋅e
where:
- n is the number of free electrons per unit volume,
- Vwire is the volume of the wire,
- e is the charge of an electron.
The volume Vwire of the wire can be calculated using its length l and the cross-sectional area A:
Vwire=A⋅l
For a wire with a circular cross-section, the area A is given by:
A=πr2
Thus,
Vwire=πr2⋅l
Substituting Vwire into the charge equation gives:
Q=n⋅(πr2⋅l)⋅e
The electric field E in the wire can be related to the potential difference V and the length l of the wire:
E=Vl
The drift velocity vd of the electrons can be expressed in terms of mobility μ and electric field E:
vd=μ⋅E=μ⋅Vl
The current I can also be expressed in terms of the drift velocity and the cross-sectional area:
I=n⋅A⋅e⋅vd
Substituting A=πr2 and vd=μ⋅Vl into the equation gives:
I=n⋅(πr2)⋅e⋅(μ⋅Vl)
Thus, the final expression for the electric current flowing through the wire is:
I=n⋅πr2⋅e⋅μ⋅Vl
Topper's Solved these Questions
- CURRENT ELECTRICITYBook:MODERN PUBLICATIONChapter:CURRENT ELECTRICITYExercise:PRACTICE PROBLEMS
Explore 71 Videos
- CURRENT ELECTRICITYBook:MODERN PUBLICATIONChapter:CURRENT ELECTRICITYExercise:CONCEPTUAL QUESTIONS
Explore 35 Videos
- ATOMS Book:MODERN PUBLICATIONChapter:ATOMS Exercise:Chapter Practice Test
Explore 16 Videos
- DUAL NATURE OF RADIATION AND MATTER Book:MODERN PUBLICATIONChapter:DUAL NATURE OF RADIATION AND MATTER Exercise:CHAPTER PRACTICE TEST
Explore 15 Videos
Similar Questions
A current I is passed through a silver strip of width d and area of cross-section A. The number of free electrons per unit volume is n
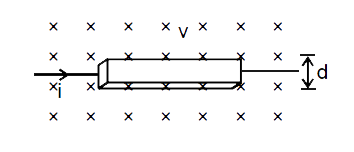
Find the drift velocity v of the electrons.
View SolutionA current I is passed through a silver strip of width d and area of cross-section A. The number of free electrons per unit volume is n
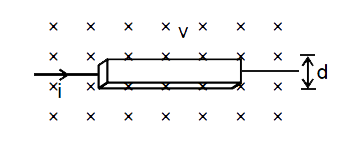
Due to the magnetic force, the free electrons get accumulated on one side of the conductor along its length. This produces a transverse electric field in the conductor which opposes the magnetic force on the electrons. Find the magnitude of the electric field which will stop further accumulation of electrons.
View Solution
Knowledge Check
A conductor of length of l and area of cross section A has n number of electrons per unit volume of the conductor. The total charge carried by the conductor is
AnA/eBenAlCnAleDn⋅eA conductor of length l and area of cross-section A has n number of electrons per unit volume of the conductor. The current flowing through conductor in time t is given by
AI=nAletBI=nAlCI=enAltDI=netIf there are n free electrons per unit volume in a conductor, if μ represents the mobility of conductor the resistivity of the conductor is
Aμ≠BμneC1μ≠D≠μ
A currrent I is passed through a silver strip of width d and area of cross section A. The number of free electrons per unit volume is n. (a) Find the drift velocity v of the electrons. (b) If a magnetic field B exists in the region as shown in what is the average magnetic force on the free electrons? (c) Due to the magnetic force, the free electrons get accumulated on one side of the conductor along its length. This produces a transverse electric field in the conductor which opposes the magnetic force on the electrons. Find the magnitude of the electric field which will be the potential diference developed across the width of the conductor due to the electron- accumulation? The appearance of a transverse emf, when a current-carrying wire is placed in a magnetic field, is called hall effect.

View SolutionThere is a current of 40 ampere in a wire of 10−6m2 are of cross-section. If the number of free electron per m3 is 1029 then the drift velocity will be
View SolutionThere is a current of 40 A in a wire 10−6m2 area of cross-section. If the number of free electrons per cubic metre is 1029, then the drift velocity is :
View SolutionA current i passes through a wire of length l , radius of cross-section r and resistivity ρ . The rate of heat generation is
View SolutionThere is a current of 40 ampere in a wire of 10−6m2 are of cross-section. If the number of free electron per m3 is 1029 then the drift velocity will be
View Solution

