Space between tow concentric spheres of radii r1andr2 such that r1<r2 is filled with a material of resistivity ρ. Find the resistance between inner and outer surface of the material
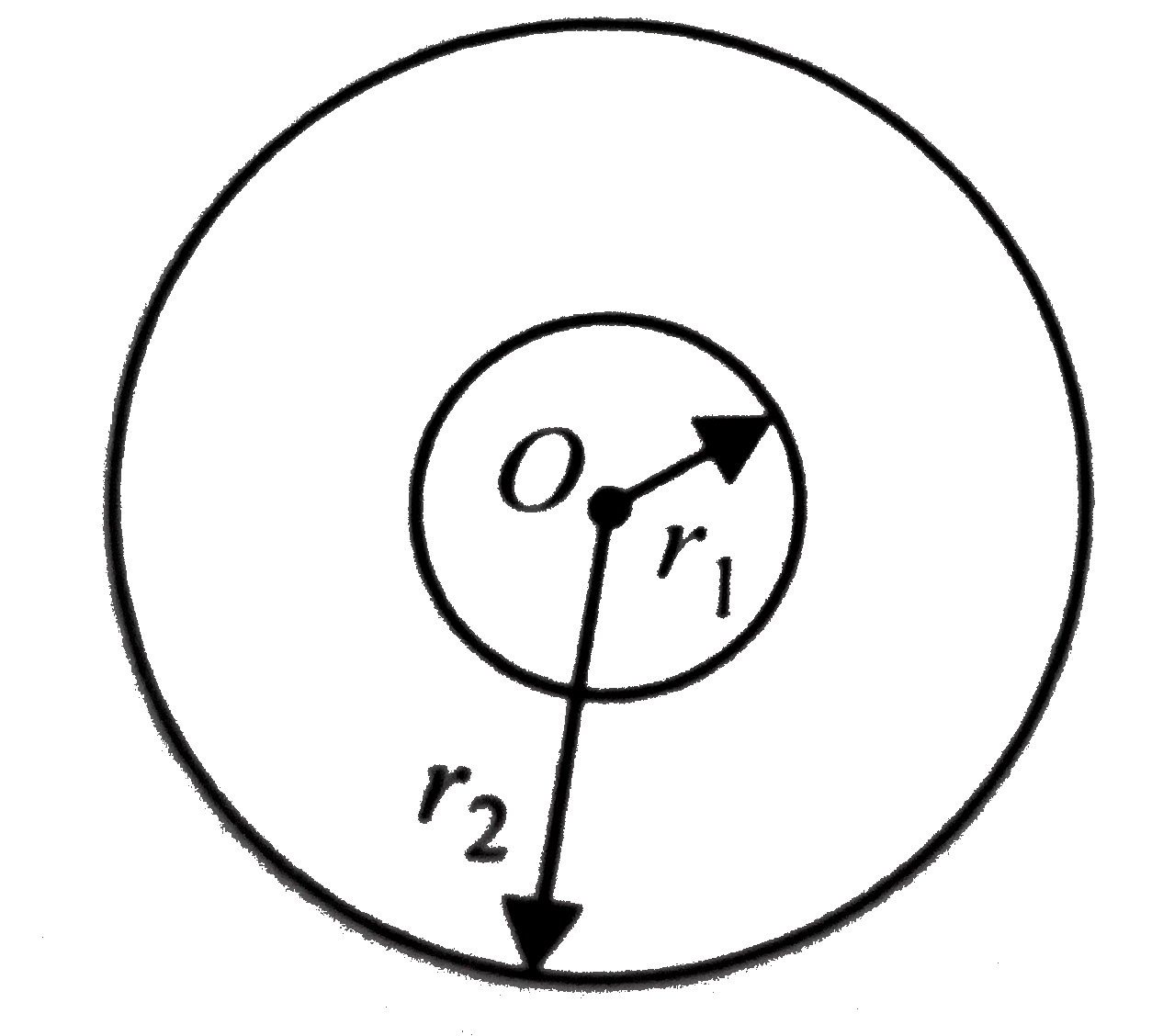
r1r2p2
r2−r1r1r2p4π
r1r2r2−r1p4π
none of these.
The correct Answer is:B
Since, R=ρla∴R=ρ=dl4πl2 (where l is any radius and dl is small element).
R=ρ4πr2∫r1dll2=ρ4π[−1l]r2r1=ρ4π[1r1−1r2]
R=[r2−r1r1r2]ρ4π
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - NCERT FINGERTIPSCHAPTER - CURRENT ELECTRICITYEXERCISE - Drift Of Electrons And The Origin Of Resistivity
2 Videos
- CURRENT ELECTRICITYBOOK - NCERT FINGERTIPSCHAPTER - CURRENT ELECTRICITYEXERCISE - Limitations Of Ohm'S Law
4 Videos
- CURRENT ELECTRICITYBOOK - NCERT FINGERTIPSCHAPTER - CURRENT ELECTRICITYEXERCISE - Electric Current In Conductors
2 Videos
- COMMUNITCATION SYSTEMSBOOK - NCERT FINGERTIPSCHAPTER - COMMUNITCATION SYSTEMSEXERCISE - HOTS
10 Videos
- DUAL NATURE OF RADIATION AND MATTER BOOK - NCERT FINGERTIPSCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - Assertion And Reason
15 Videos
Similar Questions
There are two concentric spheres of radius a and b respectively. If the space between them is filled with medium of resistivity ρ, then the resistance of the intergap between the two spheres will be (Assume b>a)
View SolutionConsider two concentric spherical metal shells of radii r1 and r2(r2>r1). Find the charge on the inner shell and charge distribution.
View Solution
Knowledge Check
The capacitance of two concentric spherical shells of radii R1 and R2(R2>R1) is
A4πε0R2B4πε0(R2−R1)R1R2C4πε0R1R2(R2−R1)D4πε0R1Sphere of inner radius a and outer radius b is made of p uniform resistivity find resistance between inner and outer surface
Ap4π(1a−1b)Bp2π(1a−1b)Cp3π(2a−1b)Dp2π(22a−1b)A metallic sphere having inner and outer radii a and b respectively has thermal conductivity
K=K0r(a≤r≤b)
Find the thermal resistance between inner surface and outer surface.A(b−a)4πK0B(b2−a2)4πKaabC4πK0(b−a)Dnone of these
Two thin metallic spherical shells of radii r1andr2(r1<r2) are placed with their centres coinciding. A material of thermal conductivity K is filled in the space between the shells. The inner shells. Is maintained at temperature θ1 .and the outer shell at temperature θ2(θ1<θ2). Calculate the rate at which heat flows radially through the material.

View SolutionTwo thin conectric shells made of copper with radius r1 and r2(r2>r1) have a material of thermal conductivity K filled between them. The inner and outer spheres are maintained at temperature TH and TC respectively by keeping a heater of power P at the centre of the two sphers. Find the value of P.
View SolutionTwo concentric, thin metallic spheres of radii R1 and R2 (R1>R2) bear charges Q1 and Q2 respectively. Then the potential at distance r between R1 and R_(2) will be
View SolutionTwo thin concentric shells made from copper with radiusr1andr2(r2>r1) have a material of thermal conductivity K filled between them. The inner and outer spheres are maintained at temperatures THandTC respectively by keeping a heater of power P at the centre of the two spheres. Find the value of P.
View SolutionConsider two concentric spherical metal shells of radii r1 and r2(r2>r1). If the outer shell has a charge q and the inner one is grounded, then the charge on the inner shell is
View Solution
