The current density varies radical distance r as J=ar2, in a cylindrical wire of radius R. The current passing through the wire between radical distance R/3andR/2 is,
65πaR42592
25πaR472
65πa2R32938
81πa2R4144
The correct Answer is:A
Current density J=ar2
Current l=∫JdA
l=R/2∫R/3ar2(2πrdr),(wheredA=2πrdr)
=2πa[r44]R/2R/3=65πaR42592
Topper's Solved these Questions
- CURRENT ELECTRICITYBook:NCERT FINGERTIPSChapter:CURRENT ELECTRICITYExercise:Drift Of Electrons And The Origin Of Resistivity
Explore 2 Videos
- CURRENT ELECTRICITYBook:NCERT FINGERTIPSChapter:CURRENT ELECTRICITYExercise:Limitations Of Ohm'S Law
Explore 4 Videos
- CURRENT ELECTRICITYBook:NCERT FINGERTIPSChapter:CURRENT ELECTRICITYExercise:Electric Current In Conductors
Explore 2 Videos
- COMMUNITCATION SYSTEMSBook:NCERT FINGERTIPSChapter:COMMUNITCATION SYSTEMSExercise:HOTS
Explore 10 Videos
- DUAL NATURE OF RADIATION AND MATTER Book:NCERT FINGERTIPSChapter:DUAL NATURE OF RADIATION AND MATTER Exercise:Assertion And Reason
Explore 15 Videos
Similar Questions
A cylindrical wire if radius R = 2 mm is of uniform area of cross-section. The current density through a cross-section varies with radial distance r as J=ar2, where a=3.2×1011A/m2 and r is in metres. What is the current through the outer portion of the wire between radial distances R/2 and R?
View SolutionThe current density ¯¯¯J inside a long, solid cylindrical wire of radius a=12mm is in the direction of the central axis, and its magnitude varies linearly with radial distance r from the axis according to J=J0ra, where J0=1054πA/m2. Find the magnitude of the magnetic field at r=a2 in μT
View Solution
Knowledge Check
The current density varies radical distance r as J=ar2, in a cylindrical wire of radius R. The current passing through the wire between radical distance R/3andR/2 is,
A65πaR42592B25πaR472C65πa2R32938DNone of theseThe current density in a wire of radius a varies with radial distance r as J=J0r2a, where J0 is a constant. Choose the incorrect statement.
ATotal current passing through the cross-section of the wire isI=πJ0a32BTotal current passing through the cross-section of the wire isI=3πJ0a32CThe field at a distance r gt a is B=μ0J0a34rDThe field at a distance r gt a is B=μ0J0a34aElectric current is passing uniformly through a solid cylindrical wire of radius R. The current I passing through circular cross-section of radius r measured from the axis of the cylinder (r<R) varies as shown in
A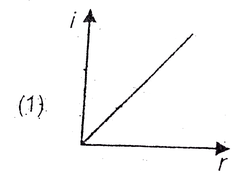 B
B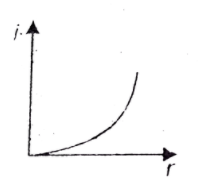 C
C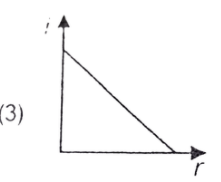 D
D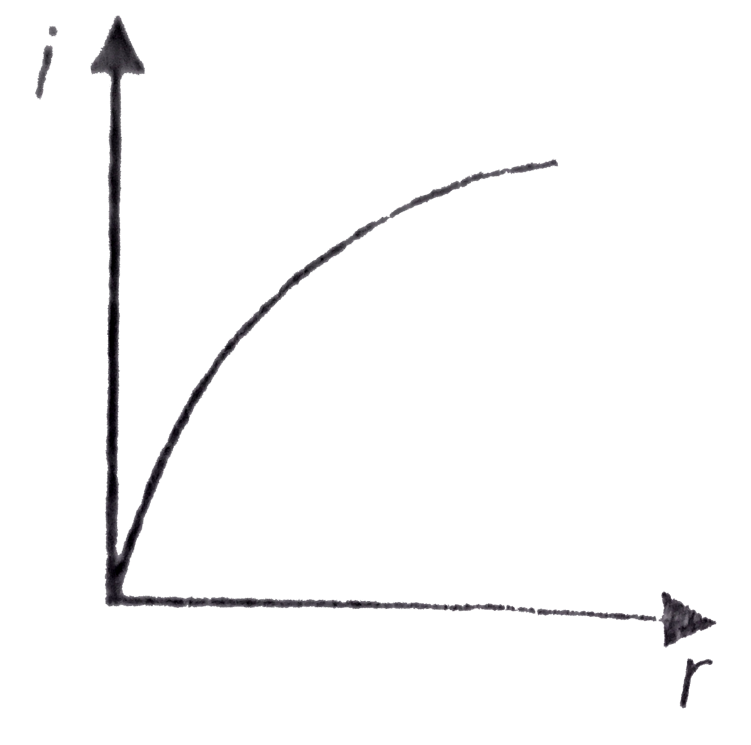
(a) The current density in a cylindrical wire of radius R=2.0mm is uniform across a cross section of the wire and is J=2.0×105A/m2. What is the current through the outer portion of the wire between radial distances R/2 and R?
(b) Suppose, instead, the current density through a cross section varies with radial distance r as J=ar2, in which a=3.0×1011A/m4 and r is in meters. What now is the current through the same outer portion of the wire?
View SolutionA long cylindrical conductor of radius R carries a current i as shown in the figure. The current density J varies across the cross-section as J=kr2, where, k is a constant. Find an expression for the magnetic field B at a distance r(<R) from the axis
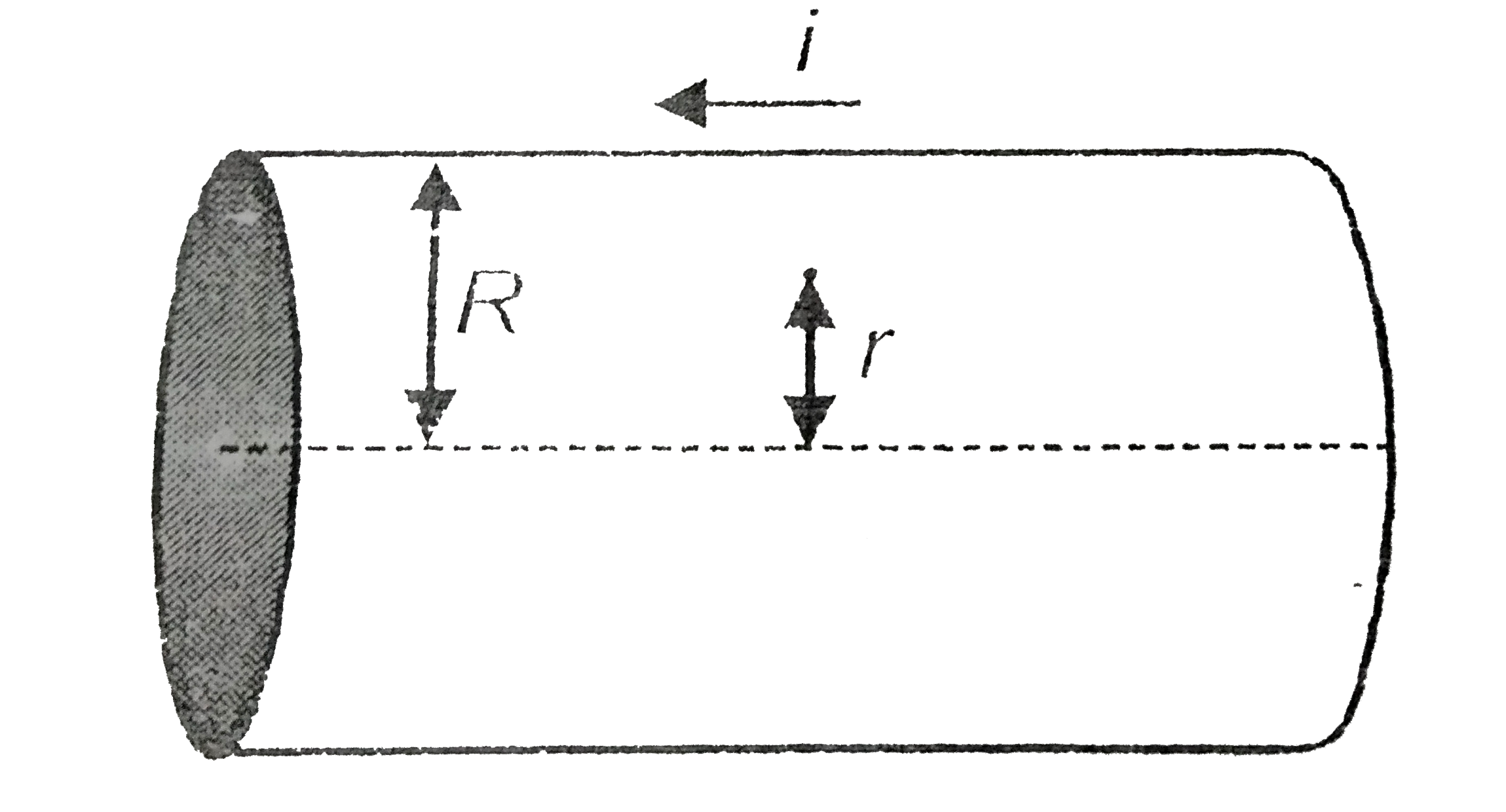
View SolutionThe current density across a cylindrical conductor of radius R varies in magnitude according to the equation J=J0(1−rR) where r is the distance from the central axis. Thus, the current density is a maximum J0 at that axis (r = 0) and decreases linearly to zero at the surface (r = R). Calculate the current in terms of J0 and the conductor 's cross - sectional area A=πR2.
View SolutionA non-homogeneous cylinder of radius "R" carries a current I whose current density varies with the radial "distance "r" from the centre of the rod as J=σr where σ is a constant.The magnetic field at a point "P" at a distance r<R from the centre of the rod is
View SolutionA:Current density is a very is a vector quantity .
R : Electric current , passing through a given unit area is current density.
View Solution
