A long cylindrical conductor of radius R carries a current i as shown in the figure. The current density J varies across the cross-section as J=kr2, where, k is a constant. Find an expression for the magnetic field B at a distance r(<R) from the axis

Consider an Amperian loop of radius r as shown. The distribution of current shows that the field will be same everywhere on the Amperian loop
∴O∫→B.→dl=B(2πr)
Now ∮→B.→dl=μ0ienc (by Ampere circuital law)
⇒B=μ0ienc2πr. To find current enclosed, consider a ring of radius x and thickness dx.
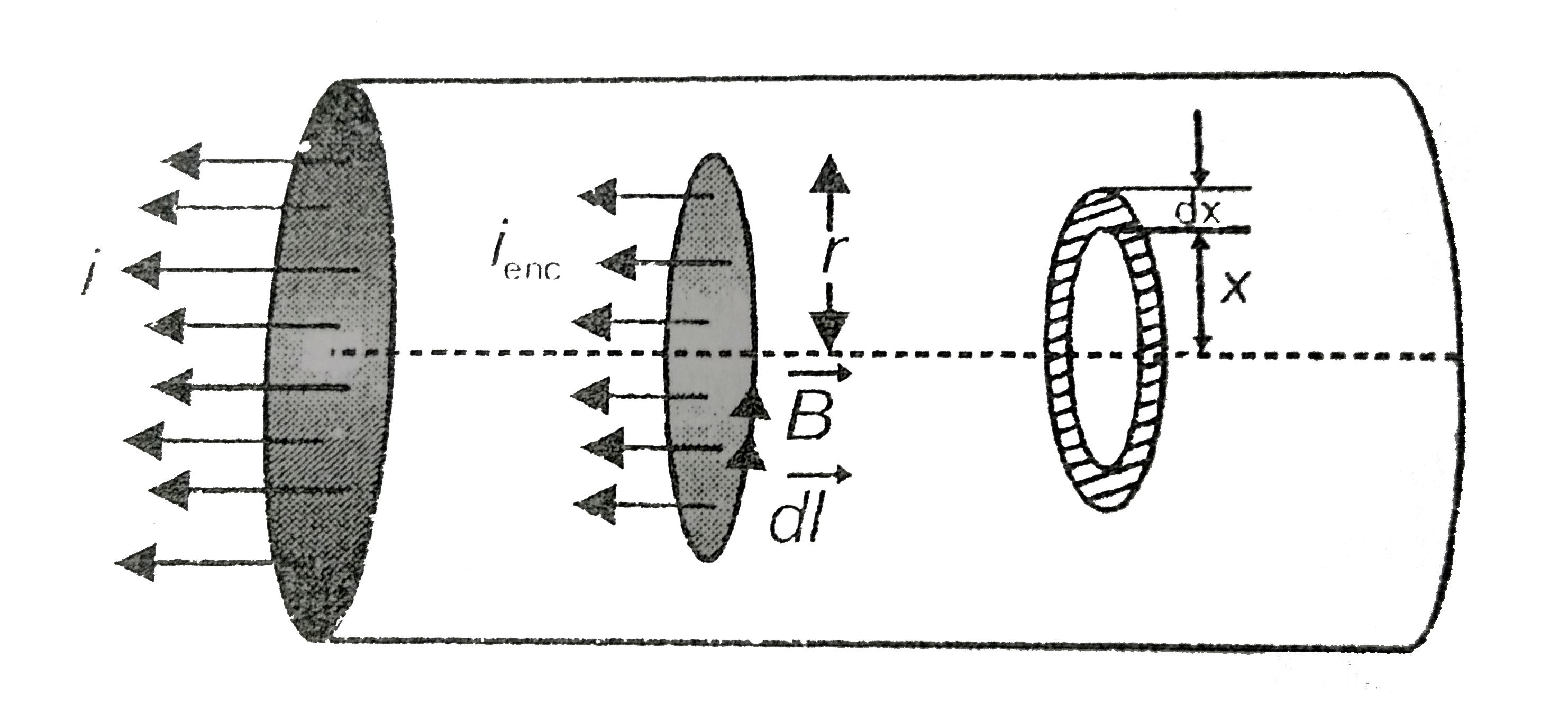
As ienc=∫J×dA=∫r0kx2×2π×dx
⇒ienc=k×2πr44
⇒B=μ0kr34
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISMBOOK - AAKASH INSTITUTECHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - Illustration
12 Videos
- MOVING CHARGES AND MAGNETISMBOOK - AAKASH INSTITUTECHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - Try Yourself
27 Videos
- MOVING CHARGE AND MAGNESIUMBOOK - AAKASH INSTITUTECHAPTER - MOVING CHARGE AND MAGNESIUMEXERCISE - SECTION D
16 Videos
- NUCLEIBOOK - AAKASH INSTITUTECHAPTER - NUCLEIEXERCISE - ASSIGNMENT (SECTION-D)
10 Videos
Similar Questions
A long cylidrical conductor of radius R carries a current i as shown in figure. The current desity J is a function of radius according to J=br, where b is a constant. Find an expression for the magnetic field B

a. at a distasnce r1<R and
b.at a distance r2>R, measured from the axis.
View SolutionA solid cylindrical conductor of radius R carries a current along its length.The current density J1 however, is not unifrom over the cross section of the conductor but is a function of the radius according to J=br, where b is a constant.the magnetic field B at r1<R is μ0br21N.Then find value of N
View Solution
Knowledge Check
A long cylindrical conductor of radius R carries I as shown. The current density is a function of radius r as j = br, where b is a constant. The magnetic field at a distance r1(r1<R) is
 Aμ0br212Bμ0br312Cμ0br213Dzero
Aμ0br212Bμ0br312Cμ0br213DzeroConsider an infinite long cylinderical conductor of radius R carrying a current I with a non uniform current density J=αr where a is a constant. Find the magnetic field for inside and outside prints.
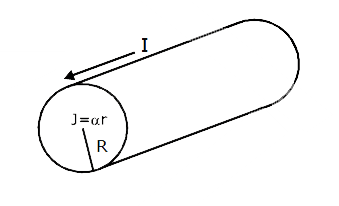 AInside αu03r2BOutside αu03Rr3Cinside the outer conductor αμ03R2DOutside αμ03rR3
AInside αu03r2BOutside αu03Rr3Cinside the outer conductor αμ03R2DOutside αμ03rR3A long straight wire of a circular cross-section (radius a) carries a steady current I and the current I is uniformly distributed across this cross-section. Which of the following plots represents the variation of magnitude of magnetic field B with distance r from the centre of the wire?
A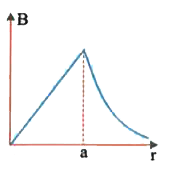 B
B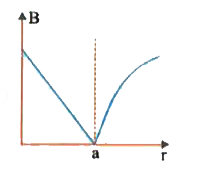 C
C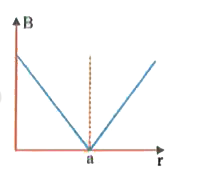 D
D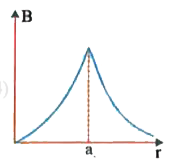
Suppose that the current density in a wife of radius a varies with r according to J=Kr2, where K is a constant and r is the distance from the axis of the wire. Find the megnetic field at a point distance r from the axis when (a) r < a and (b) r > a

View SolutionA non-homogeneous cylinder of radius "R" carries a current I whose current density varies with the radial "distance "r" from the centre of the rod as J=σr where σ is a constant.The magnetic field at a point "P" at a distance r<R from the centre of the rod is
View SolutionFigure shows a long straight wire of a circular cross-section (radius a) carrying steady current l. The current l is uniformly distributed across this cross-section. Calculate the magnetic field in the region r<aandr>a

View SolutionIf the current density in a linear conductor of radius 'a' varies with r according to relation J=kr2, where k is a constant and r is the distance of a point from the axis of conductor. Find the magnetic field induction at a point distance r from the axis, when (i) r<a and (ii) r>a.
View SolutionA long straight cylindrical region of radius a curries a current along its length. The current density (J) varies from the axis to the edge of the cylindrical region according to J=J0(1–ra) Where r is distance from the axis (0<r<a)
(a) Find the mean current density.
(b) Plot the variation of magnetic field (B) with distance r from the axis of the cylinder for 0<r<a.
View Solution
