A horizontally oriented uniform disc of mass M and radius R rotates freely about a stationary vertical axis passing through its centre. The disc has a radial guide along which can slide without friction a small body of mass m. A light thread running down through the hollow axle of the disc is tied to the body initially the body was located at the edge of the disc and the whole system rotated with ann angular velocity ω0. Then by means of a force F applied to the lower and of the thread the body was slowly pulled to the rotation axis. find:
(a). The angular velocity of the system in its final state.
(b). The work performed by the force F.
(a). I1ω2=I2ω2
∴ω2=(I1I2)ω1=(12MR2+mR2)(12mR2)ω0
=(1+2mM)ω0
(b). W=Kf−Ki
=12I2ω22−12I1ω21
=12[12MR2][1+2mM]2ω20−12
[12MR2+mR2]ω20
=14MR2(1+2mM)ω20[1+2mM−1]
=12mω20R2(1+2mM)
Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 2 Single Correct
26 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 2 Multiple Correct
36 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 1 Objective
30 Videos
- ROTATIONBOOK - DC PANDEYCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises
39 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEYCHAPTER - ROTATIONAL MOTIONEXERCISE - Integer Type Questions
17 Videos
Similar Questions
A uniform disc of mass m and radius R rotates about a fixed vertical axis passing through its centre with angular velocity ω. A particle of same mass m and having velocity of 2ωR towards centre of the disc collides with the disc moving horizontally and sticks to its rim. Then
View SolutionA man of mass m stands on the edge of a horizontal unifom disc of mass M and radius R whichis capable of rotating freely about a stationary vertical axis passing through its center. At a certain moment the man starts moving along the edge of the disc, he shifts over angle θ relative to the disc and then stops. Find the angle through which the disc rotates.
View Solution
Knowledge Check
A uniform disc of mass M and radius R is pivoted about a horizontal axis passing through its edge. It is released from rest with its centre of mass at the same height as the pivot.
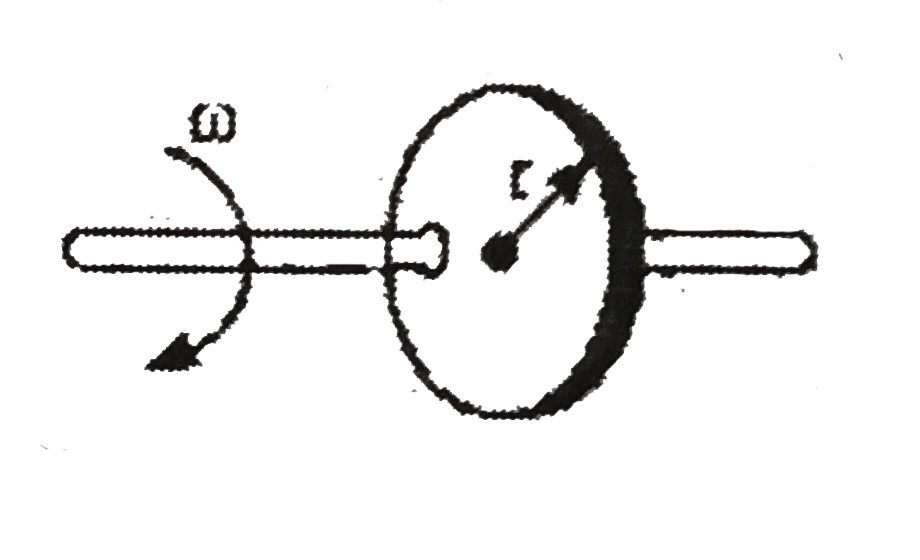 AThe angular velocity of disc when its centre of mass is directly below the pivot is √4g3rBThe force exerted by the pivot at this instant is 73mgCAngular momentum of disc is conservedDAngular acceleration of disc at the given instant is zero
AThe angular velocity of disc when its centre of mass is directly below the pivot is √4g3rBThe force exerted by the pivot at this instant is 73mgCAngular momentum of disc is conservedDAngular acceleration of disc at the given instant is zeroThe M.I. of a uniform semicircular disc of mass M and radius R about a line perpendicular to the plane of the disc and passing through the centre is
A12MR2B14MR2CMR2D34MR2A uniform disc of mass M and radius R is rotating about a horizontal axis passing through its centre with angular velocity ω . A piece of mass m breaks from the disc and flies off vertically upwards. The angular speed of the disc will be
A(M−2m)ω(M−m)B(M+2m)ω(M+m)C(M−2m)ω(M+m)D(M+2m)ω(M−m)
A man of mass m1 stands on the edge of a horizontal uniform disc of mass m2 and radius R which is capable of rotating freely about a stationary vertical axis passing through its centre . The man walks along the edge of the disc through angle θ relative to the disc and then stops . find the angle through which the disc turned the time the man stopped .
[2m1θ2m1+m2]
View SolutionCalculate the moment of inertia of a disc of radius R and mass M, about an axis passing through its centre and perpendicular to the plane.
View SolutionThe M.I. of disc of mass M and radius 'R' about an axis passing through midway between centre and circumference and perpendicular to its plane is
View SolutionA uniform disc of mass m and radius R rotates about a fixed vertical axis passing through its centre with angular velocity ω. A particle of same angular velocity mass m and moving horizontally with velocity 2ωR towards centre of the disc collides and sticks to its rim. The impulse on the particle due to the disc is
View SolutionThe moment of inertia of a uniform semicircular disc of mass M and radius r about a line perpendicular to the plane of the disc through the center is
View Solution
